第七章 5 探究弹性势能的表达式
卷紧的发条、拉长或压缩的弹簧、拉开的弓、正在击球的网球拍、撑杆跳高运动员手中弯曲的杆,等等,这些物休都发生了弹性形变,每个物体的各部分之间都有弹力的相互作用。[1]
发生弹性形变的物体的各部分之间,由于有弹力的相互作用,也具有势能,这种势能叫做弹性势能(elastic potential energy)。

在讨论重力势能的时候,我们先分析重力做功的情况,由此入手得出了重力势能的表达式。在探究弹性势能的表达式时,可以参考对重力势能的讨论,先分析弹力做功的情况。
当弹簧的长度为原长时,它的弹性势能为0,弹簧被拉长或被压缩后,就具有了弹性势能。我们以弹簧被拉长的情况为例,探究弹性势能的表达式。
在探究的过程中,要依次解决下面几个问题。
(1)弹性势能的表达式可能与哪几个物理量有关?
重力势能与物体被举起的高度h有关,所以弹性势能很可能与弹簧被拉伸的长度l有关。有什么样的关系?重力势能Ep与高度h成正比例,对于弹性势能,尽管也会是“拉伸的长度越大,弹簧的弹性势能也越大”,但会是正比例关系吗?不一定,因为对于同一个弹簧,拉得越长,所用的力就越大,而要举起同一个重物,所用的力并不随高度变化。

图7.5-2 弹力与重力的变化规律不一样,弹性势能与重力势能的表达式很可能也不一样。
即使拉伸的长度l相同,不同弹簧的弹性势能也不会一样,因为不同弹簧的“软硬”并不一样,即劲度系数k不同。这点也应在弹性势能的表达式中反映出来,而且应该是,在拉伸长度l相同时,k越大,弹性势能越大。
这两个猜测并不能准确地告诉我们弹性势能的表达式,但如果探究的结果与这些猜测相矛盾,意味着很可能出现了错误,需要慎重地“评估”探究的各个环节。
(2)弹簧的弹性势能与拉力做的功有什么关系?
我们一贯的思想是:研究做功对某种能量的影响,从而了解这种能量。在这个问题中则是考虑,怎样由拉力做的功得出弹性势能的表达式。
(3)怎样计算拉力做的功?
在地面附近,重力的大小、方向都相同,所以不管物体移动的距离大小,重力做的功都可以简单地用重力与物体在竖直方向移动距离的乘积来表示。
对于弹力,情况要复杂些。弹簧拉伸的距离l越长,拉力F越大,即
F=kl
这时不妨利用以前计算匀变速直线运动物体位移的经验。那时候想用速度与时间相乘得到位移,但速度在变化,于是我们把整个运动过程划分成很多小段,每个小段中物体速度的变化都很小,可以近似地用小段中任意一个时刻的速度与这个小段时间间隔相乘得到这小段位移的近似值,然后把各小段位移的近似值相加。当各小段分得非常非常小时,得到的就是匀变速直线运动的位移表达式了。
请复习《物理必修l》第二章第3节。
对于弹力做功,可以用类似的方法做如下处理。
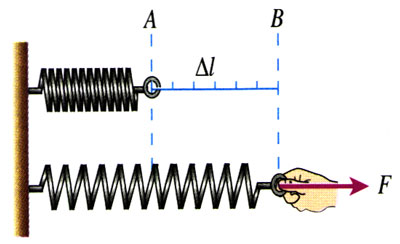
如图7.5-3,弹簧从A拉伸到B的过程被分成很多小段,它们的长度是
Δl1,Δl2,Δl3,…
在各个小段上,拉力可以近似认为是不变的,它们分别是
F1,F2,F3,…
所以,在各个小段上,拉力做的功分别是
F1Δl1,F2Δl2,F3Δl3,…
拉力在整个过程中做的功可以用它在各小段做功之和来代表
F1Δl1+F2Δl2+F3Δl3+…
(4)怎样计算这个求和式?
在处理匀变速直线运动的位移时,我们曾经利用v-t图象下梯形的面积来代表位移,这里是否可以用F-l图象下一个梯形的面积来代表功?
……
沿着这样的思路,你可以通过自己的探究得到弹性势能的表达式。
[1] 学习这节时,要着重体会探究的过程和所用的方法,复习用到的知识,不要求掌握探究的结论,更不要求用弹性势能的表达式解题。
发布时间:2016/12/16 上午7:19:45 阅读次数:5433
