第七章 4 重力势能

这一节我们定量地研究重力势能，为此首先要确定重力势能的表达式。

正如前述，物体由于被举高而具有重力势能，它的质量越大、所处的位置越高，重力势能就越大。重力势能的表达式应该符合这些特征。

另一方面，当物体的高度发生变化时，重力要做功：物体下降时重力做正功；物体被举高时重力做负功。因此，认识重力势能不应脱离对重力做功的研究。

重力做的功

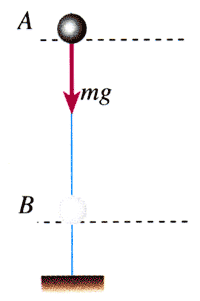
设一个质量为m的物体，从高度是h₁的位置，竖直向下运动到高度是h₂的位置，如图7.4-1，这个过程中重力做的功是

W_G＝mgh＝mgh₁－mgh₂

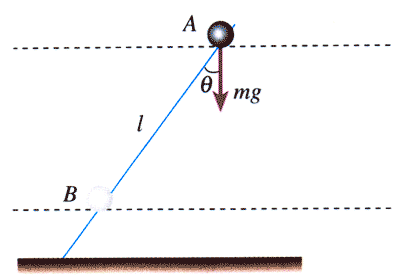
再看另一种情况。质量为m的物体仍然从上向下运动，高度由由h₁降为h₂，但这次不是沿竖直方向，而是沿着倾斜的直线向下运动，如图7.4-2。

物体沿倾斜直线运动的距离是l，在这一过程中重力做的功是

W_G＝mgcosθ·l＝mgh＝mgh₁－mgh₂

上面两种情况中，尽管物体运动的路径不同，但高度的变化是一样的，而且重力做的功也是一样的。

假设所说“倾斜的直线”是个斜面，斜面是否光滑对计算“重力做的功”有影响吗？

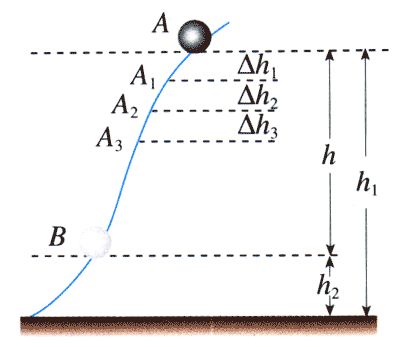
假设这个物体沿任一路径由高度是h₁的起点A，运动到高度是h₂的终点B，如图7.4-3。我们把整个路径分成许多很短的间隔

AA₁，A₁A₂，A₂A₃，…

由于每一段都很小，因而都可以近似地看做一段倾斜的直线。设每段小斜线的高度差分别是

Δh₁，Δh₂，Δh₃，…

则物体通过每段小斜线时重力做的功分别为

mgΔh₁，mgΔh₂，mgΔh₃，…

物体通过整个路径时重力做的功，等于重力在每小段上所做的功的代数和，即

W_G＝mgΔh₁＋mgΔh₂＋mgΔh₃＋…

＝mg（Δh₁＋Δh₂＋Δh₃＋…）

＝mgh

＝mgh₁－mgh₂

这里的分析表明，物体运动时，重力对它做的功只跟它的起点和终点的位置有关，而跟物体运动的路径无关，功的大小等于物重跟起点高度的乘积mgh₁与物重跟终点高度的乘积mgh₂两者之差。

看起来，物体所受的重力mg与它所处位置的高度h的乘积“mgh”，是一个具有特殊意义的物理量。

重力势能

mgh这个物理量的特殊意义在于它一方面与重力做的功密切相关，另一方面它随着高度的增加而增加、随着质量的增加而增加，恰与势能的基本特征一致。因此，我们把物理量mgh叫做物体的重力势能（gravitational potential energy），常用E_p表示，即

E_p＝mgh                      （1）

上式表明，物体的重力势能等于它所受重力与所处高度的乘积。

与其他形式的能一样，重力势能也是标量，其单位与功的单位相同，在国际单位制中都是焦耳，符号为J。

1 J＝1kg·m·s^-2·m＝1 N·m

有了重力势能的表达式，重力做的功与重力势能的关系可以写为

W_G＝E_p1－E_p2       （2）

其中E_p1＝mgh₁表示物体在初位置的重力势能，E_p2＝mgh₂表示物体在末位置的重力势能。

当物体由高处运动到低处时，重力做正功，重力势能减少，也就是W_G＞0，E_p1＞E_p2。重力势能减少的数量等于重力做的功。

当物体由低处运动到高处时，重力做负功（物体克服重力做功），重力势能增加，也就是W_G＜0，E_p1＜E_p2。重力势能增加的数量等于物体克服重力所做的功。

说一说

如果重力做的功与路径有关，即对应于同样的起点和终点，重力对同一物体所做的功，随物体运动路径的不同而不同，我们还能把mgh叫做物体的重力势能吗？为什么？

重力势能的相对性

物体的高度h总是相对于某一水平面来说的，实际上是把这个水平面的高度取做0。因此，物体的重力势能也总是相对于某一水平面来说的，这个水平面叫做参考平面。在参考平面，物体的重力势能取做0。

选择哪个水平面做参考平面，可视研究问题的方便而定。通常选择地面为参考平面。

选择不同的参考平面，物体重力势能的数值是不同的，但这并不影响问题的研究，因为在与重力势能相关的问题中，有价值的是势能的差值，而选择不同的参考平面对这个差值没有影响。

对选定的参考平面而言，上方物体的高度是正值，重力势能也是正值；下方物体的高度是负值，重力势能也是负值。负值的重力势能，表示物体在这个位置具有的重力势能要比在参考平面上具有的重力势能小。

势能是系统所共有的

必须指出的是，重力势能跟重力做功密切相关，而重力是地球与物体之间的相互作用力。也就是说，倘若没有地球，就谈不上重力。所以，严格说来，重力势能是地球与物体所组成的物体“系统”所共有的，而不是地球上的物体单独具有的。

除了重力势能，还有其他形式的势能。任何形式的势能，都是物体系统由于其中各物体之间，或物体内的各部分之间存在相互作用（力）而具有的能，是由各物体的相对位置决定的。例如，分子之间由于存在相互作用而具有势能，叫做分子势能，由分子间的相对位置决定；电荷之间由于存在相互作用而具有势能，叫做电势能，由电荷间相对位置决定。分子势能或电势能分别属于分子或电荷组成的系统，不是一个分子或一个电荷单独具有的。

问题与练习

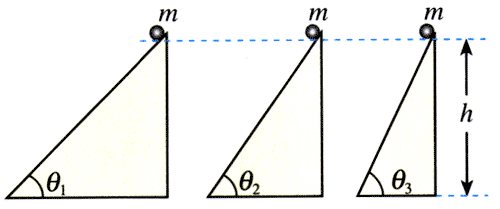
1．图7.4-8中的几个斜面，它们的高度相同、倾角不同。让质量相同的物体沿斜面从顶端运动到底端。试根据功的定义计算沿不同斜面运动时重力做的功，以证明这个功与斜面的倾角无关。

2．如图7.4-9，质量为m的足球在地面1的位置被踢出后落到地面3的位置，在空中达到的最高点2的高度为h。

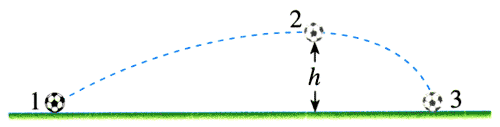
（1）足球由位置l运动到位置2时，重力做了多少功？足球克服重力做了多少功？足球的重力势能增加了多少？

（2）足球由位置2运动到位置3时，重力做了多少功？足球的重力势能减少了多少？

（3）足球由位置l运动到位置3时，重力做了多少功？足球的重力势能变化了多少？

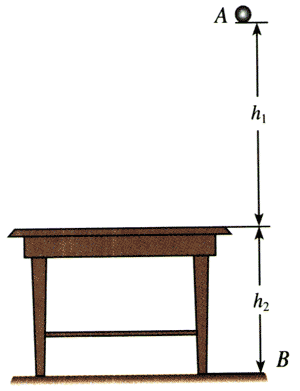
3．如图7.4-10，质量m＝0.5 kg的小球，从桌面以上高h₁＝1.2m的A点下落到地面的B点，桌面高h₂＝0.8m。

（1）在表格的空白处按要求填入数据。

（2）如果下落时有空气阻力，表格中的数据是否应该改变？

4．以下说法是否正确？如果正确，说出一种可能的实际情况；如果不正确，说明这种说法为什么错。

（A）物体受拉力作用向上运动，拉力做的功是1J，但物体重力势能的增加量不是1J。

（B）物体受拉力作用向上匀速运动，拉力做的功是1J，但物体重力势能的增加量不是1J。

（C）物体运动，重力做的功是－1J，但物体重力势能的增加量不是1J。

（D）没有摩擦时物体由A沿直线运动到B，克服重力做的功是1J，有摩擦时物体由A沿曲线运动到B，克服重力做的功大于1J。

发布时间：2016/12/15 上午7:19:22  阅读次数：1756