第七章 2 功

人类对于能量及其转化的认识与功的概念紧密相连。这是因为在一个过程中如果既存在做功的现象，也存在能量变化的现象，功的计算常常能够为能量的定量表达及能量的转化提供分析的基础。

功

功的概念起源于早期工业发展的需要。当时的工程师们需要一个比较蒸汽机效能的办法。在实践中大家逐渐认识到，当燃烧同样多的燃料时，机械举起的重量与举起高度的乘积可以用来量度机器的效能，从而比较蒸汽机的优劣，并把物体的重量与其上升高度的乘积叫做功。到了19世纪20年代，法国科学家科里奥利扩展了这一基本思想，明确地把作用于物体上的力和受力点沿力的方向的位移的乘积叫做“力的功”。

在学习初中物理时我们就已经跨越了历史的长河，认识到，一个物体受到力的作用，并在力的方向上发生了一段位移，这个力就对物体做了功（work）。起重机提起货物，货物在起重机拉力的作用下发生一段位移，拉力就对货物做了功。列车在机车的牵引力作用下发生一段位移，牵引力就对列车做了功。用手压缩弹簧，弹簧在手的压力下发生形变，也就是产生了一段位移，压力就对弹簧做了功。可见，力和物体在力的方向上发生的位移，是做功的两个不可缺少的因素。

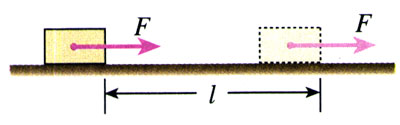
在物理学中，如果力的方向与物体运动的方向一致，如图7.2-2，我们就把功定义为力的大小与位移大小的乘积。用F表示力的大小，用l表示位移的大小，用W表示力F所做的功，则有

W＝Fl

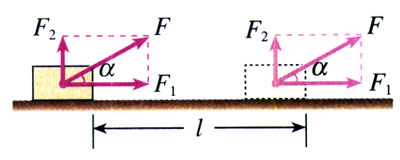
当力F的方向与运动方向成某一角度时（图7.2-3），可以把力F分解为两个分力：与位移方向一致的分力F₁，与位移方向垂直的分力F₂。设物体在力F的作用下发生的位移的大小是l，则分力F₁所做的功等于F₁l。分力F₂的方向与位移的方向垂直，物体在F₂的方向上没有发生位移，F₂所做的功等于0。因此，力F对物体所做的功W等于F₁l，而F₁＝Fcosα，所以

W＝Flcosα

这就是说，力对物体所做的功，等于力的大小、位移的大小、力与位移夹角的余弦这三者的乘积。

功是标量。在国际单位制中，功的单位是焦耳（joule），简称焦，符号是J。1J等于1N的力使物体在力的方向上发生1 m的位移时所做的功，所以

1J＝1N×1m＝1N·m

正功和负功

我们讨论一个力做功时可能出现的各种情形。

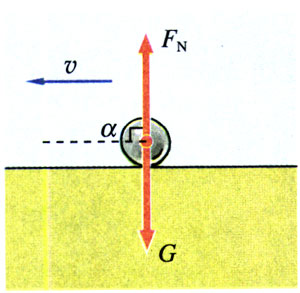
（1）当α＝\(\frac{\pi }{2}\)时，cosα＝0，W＝0。这表示力F的方向与位移l的方向垂直时，力F不做功。例如，物体在水平桌面上运动，重力G和支持力F_N都与位移方向垂直，这两个力都不做功（图7.2-4）。

（2）当α＜\(\frac{\pi }{2}\)时，cosα＞0，W＞0。这表示力F对物体做正功。例如，人用力拉车前进时，人的拉力F对车做正功（图7.2-5）。

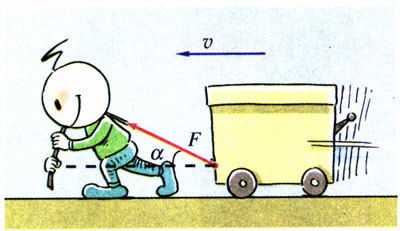
（3）\(\frac{\pi }{2}\)＜α≤π时，cosα＜0[1]，W＜0。这表示力对物体做负功。例如，推着小车跑动的人，到达目的地减速时，人向后拉车的力F对车做负功（图7.2-6）。

某力对物体做负功，往往说成“物体克服某力做功”（取绝对值）。这两种说法的意义是等同的。例如，竖直向上抛出的球，在向上运动的过程中，重力对球做负功，可以说成“球克服重力做功”。汽车关闭发动机以后，在阻力的作用下逐渐停下来，阻力对汽车做负功，可以说成“汽车克服阻力做功”。

当一个物体在几个力的共同作用下发生一段位移时，这几个力对物体所做的总功，等于各个力分别对物体所做功的代数和。可以证明，它也就是这几个力的合力对物体所做的功。

做一做

证明：几个力对一个物体做功的代数和，等于这几个力的合力对这个物体所做的功。

例题

一个质量m＝150 kg的雪橇，受到与水平方向成θ＝37°角斜向上方的拉力F＝500 N，在水平地面上移动的距离l＝5 m（图7.2-7）。雪橇与地面间的滑动摩擦力F_阻＝100 N。求力对雪橇做的总功。

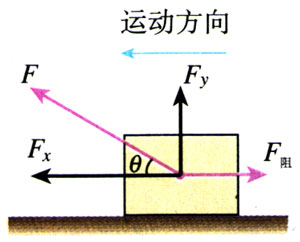
【分析】雪橇受到的重力和支持力沿竖直方向，与雪橇运动方向垂直，不做功。

拉力F可以分解为水平方向和竖直方向的两个分力，竖直方向的分力与运动方向垂直，不做功，所以力对雪橇做的总功为拉力的水平分力和阻力所做的功的代数和。

【解】拉力在水平方向的分力为F_x＝Fcos37°，它做的功为

W₁＝F_xl＝Flcos37°

摩擦力与运动方向相反，它做的功为负功

W₁＝－F_阻l

力对物体做的总功为二者的代数和，即

W＝W₁＋W₂＝Flcos37°－F_阻l

把题目所给的数值以及查表所得cos37°＝0.7986的值代入，得

W＝1 500J

力对雪橇做的总功是1500 J。

问题与练习

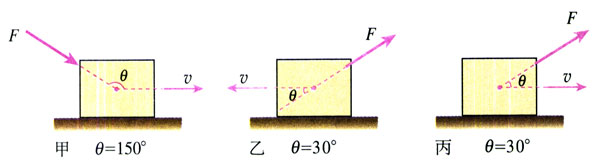
1．图7.2-8表示物体在力F的作用下在水平面上发生了一段位移x，分别计算这三种情形下力F对物体做的功。设这三种情形下力F和位移x的大小都是一样的：F＝10N，x＝2m。角θ的大小如图所示。

2．用起重机把重量为2.0×10⁴ N的物体匀速地提高了5m，钢绳的拉力做了多少功？重力做了多少功？物体克服重力做了多少功？这些力做的总功是多少？

3．一位质量m＝60 kg的滑雪运动员从高h＝10m的斜坡自由下滑。如果运动员在下滑过程中受到的阻力F＝50N，斜坡的倾角θ＝30°，运动员滑至坡底的过程中，所受的几个力做的功各是多少？这些力做的总功是多少？

4．一个重量为10N的物体，在15 N的水平拉力的作用下，一次在光滑水平面上移动0.5 m，另一次在粗糙水平面上移动相同的距离，粗糙面与物体间的动摩擦因数为0.2。在这两种情况下，拉力做的功各是多少？拉力这两次做的功是否相同？各个力对物体做的总功是否相同？

发布时间：2016/12/13 上午7:23:17  阅读次数：1939