第七章 1 追寻守恒量——能量

物理学的任务是发现普遍的自然规律。因为这样的规律的最简单的形式之一表现为某种物理量的不变性，所以对于守恒量的寻求不仅是合理的，而且也是极为重要的研究方向。

——劳厄[1]

任何人类活动都离不开能量。例如，现代化的生活离不开电厂供应的电能；现代交通离不开燃料燃烧释放的化学能；核电站要利用原子核裂变时释放的核能；人类生活需要摄入食物中的化学能；植物的生长依赖太阳能……

在长期的科学实践中，人类已经建立起各种形式的能量概念及其量度的方法，如动能、势能、电磁能、核能等等，并且发现不同形式的能量可以互相转化，在转化过程中遵从能量守恒这个基本原理。

这章我们要研究的，是动能、势能及其相互转化的规律。

第七章 1 追寻守恒量——能量

诺贝尔物理学奖获得者费恩曼曾说：“有一个事实，如果你愿意，也可以说是一条定律，支配着至今所知的一切自然现象……这条定律称做能量守恒定律。它指出：有某一个量，我们把它称为能量，在自然界经历的多种多样的变化中它不变化。那是一个最抽象的概念……”

然而，正是这个最抽象的概念，却是物理学中最重要，意义也最深远的概念之一。

能量的概念是人类在对物质运动规律进行长期探索中建立的。所有自然现象都涉及能量，人类任何活动都离不开能量：流动的江水具有动能；高处水库里的水具有势能；现代化的生活离不开电能；现代交通工具离不开燃料燃烧释放的化学能；核电站要利用原子核裂变时释放的核能；人的生命需要摄入食物中的化学能；绿色植物的生长需要太阳能……这还只是无数事例中的一小部分，可见能量无处不在，并且不同形式的能量可以互相转化。

能量对于科学事业和日常生活有着巨大的影响，但要用一句话说清楚能量究竟是什么却非易事。这也许是牛顿未能把“能量”这一概念留给我们的原因。但是在牛顿之前，我们就能在力学领域发现它的萌芽。例如，能量及其守恒的思想，在伽利略的实验中（图7.1-1）已经显现出来了。

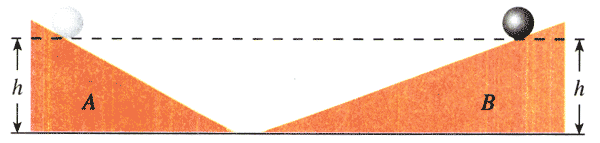
在这个实验中，小球一旦沿斜面A滚落，它就要继续滚上另一个斜面B。重要的是，伽利略发现了具有启发性的事实：无论斜面B比斜面A陡些或缓些，小球的速度最后总会在斜面上的某点变为0，这点距斜面底端的竖直高度与它出发时的高度相同。看起来，小球好像“记得”自己起始的高度，或与高度相关的某个量。然而，“记得”并不是物理学的语言，后来的物理学家把这一事实说成是“某个量是守恒的”，并且把这个量叫做能量（energy）或能。

科学概念的力量在于它具有解释和概括一大类自然现象的能力。在这方面能量概念的作用十分突出。

当伽利略把小球从桌面提高到起始点的高度时，他赋予小球一种形式的能量，我们称它为势能（potential energy）。相互作用的物体凭借其位置而具有的能量叫做势能。

伽利略释放小球后，小球开始运动，获得速度，当它到达斜面的底部时，已经处于桌面的水平面上。以前由于它在桌面上方的某一高度而具有的势能，这时已经消失，但是，小球获得了运动。这个事实可以理解为：势能并未丢失，而是转化成另一种形式的能量，我们称它为动能（kinetic energy）。物体由于运动而具有的能量叫做动能。

当小球继续沿斜面B升高时，它会变慢，因而不断失去动能；但它的高度在增加，势能不断被“回收”。当小球速度最后变为0时，小球相对桌面的高度又达到它在实验起始时的高度，其全部动能都转化成势能。

如果不采用能量的概念，我们也可以利用以前的语言来描述这个实验。我们可以说：为了把小球从桌面提高到斜面上的某个位置，伽利略施加了与重力相反的力；当他释放小球时，重力使小球滚下斜面A；在斜面的底部，小球由于惯性而滚上斜面B。

但是，这样的描述不能表达一个最重要的事实：如果空气阻力和摩擦力小到可以忽略，小球必将准确地终止于它开始运动时的高度，不会更高一点，也不会更低一点。这说明某种“东西”在小球运动过程中是不变的，这个“东西”就是能量。

能量概念的引入是科学前辈们追寻守恒量的一个重要事例。

伽利略的斜面实验使人们认识到引入能量概念的重要性，同时也提出了值得思考的问题：势能和动能如何定量地量度？如果不能回答这个问题，怎么能谈到它们的转化和守恒呢？

令人欣慰的是，在物理学的发展过程中，人们不但建立起各种形式的能量的概念，而且确定了它们的定量表达式，这是因为人们建立并不断发展了功的概念。

那么，功的概念是怎样建立的，我们又怎样计算它呢？

问题与练习

举出生活中的一个例子，说明不同形式的能量之间可以相互转化。你的例子是否向我们提示，转化过程中能的总量保持不变？

发布时间：2016/12/12 下午2:52:39  阅读次数：1389