第五章 6 向心力
向心力
做圆周运动的物体为什么不沿直线飞去而沿着一个圆周运动?那是因为它受到了力的作用。用手抡一个被绳系着的物体,它能做圆周运动,是因为绳子对它的力在拉着它。月球绕地球转动,是地球对月球的引力在“拉”着它。
做匀速圆周运动的物体具有向心加速度。根据牛顿第二定律,产生向心加速度的原因一定是物体受到了指向圆心的合力。这个合力叫做向心力(centripetal force)。
把向心加速度的表达式代入牛顿第二定律,可得向心力的表达式
Fn=m\(\frac{{{v^2}}}{r}\) (1)
或者
Fn=mω2r (2)
实验
用圆锥摆粗略验证向心力的表达式
细线下面悬挂一个钢球,细线上端固定在铁架台上。将画着几个同心圆的白纸置于水平桌面上,使钢球静止时正好位于圆心。用手带动钢球,设法使它沿纸上的某个圆周运动(图5.6-1)。
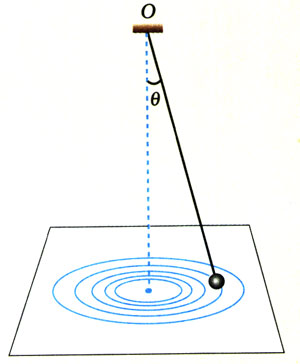
用秒表或手表记录钢球运动若干圈的时间,再通过纸上的圆测出钢球做匀速圆周运动的半径,这样就能算出钢球的线速度。钢球的质量可以由天平测出。于是,用(1)式就能算出钢球所受的向心力。
我们再从另一方面计算钢球所受的向心力。
钢球在水平面内做匀速圆周运动时,受到重为mg和细线拉力FT的作用(图5.6-2),它们的合力为F。由图中看出,F=mgtan θ。tan θ值能通过以下测量和计算得到:在图5.6-1中,测出圆半径r和小球距悬点的竖直高度h,两者之比就是tan θ。用天平测得钢球质量后,合力F的值也就得到了。
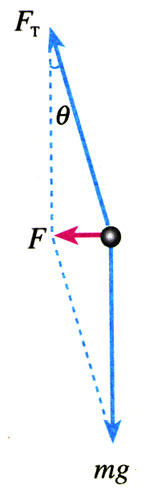
由于小球运动时距纸面有一定高度,所以它距悬点的竖直高度h并不等于纸面距悬点的高度。这点差别可以通过估算解决。此外,测量小球距悬点的竖直高度时,要以小球的球心为准。
比较两个方法得到的向心力,对你的实验的可靠性做出评估。
应该强调的是,向心力并不是像重力、弹力、摩擦力那样作为具有某种性质的力来命名的。它是根据力的作用效果命名的。凡是产生向心加速度的力,不管属于哪种性质,都是向心力。对此,我们在以上圆锥摆实验中已经有了初步的体会。
如果说圆锥摆的摆球受到了重力、绳的拉力、向心力这样三个力的作用,那就错了。实际上,它只受到重力和绳的拉力,是这两个力的合力起到了向心力的作用。
变速圆周运动和一般的曲线运动
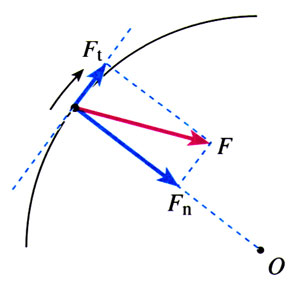
在本节后面“做一做”的实验中,我们可以改变抡绳子的方式来调节沙袋速度的大小。这就带来一个疑问:难道向心力可以改变速度的大小吗?链球运动员投掷时也有类似情况。仔细观察别人的操作,再琢磨自己的动作就能发现,我们使沙袋加速时,绳子牵引沙袋的方向并不与沙袋运动的方向完全垂直。也就是说,沙袋加速时,它所受的力并不严格通过运动轨迹的圆心。
图5.6-3表示做圆周运动的沙袋正在加速的情况。O是沙袋运动轨迹的圆心,F是绳对沙袋的拉力。根据F产生的效果,可以把F分解为两个相互垂直的分力:跟圆周相切的分力Ft和指向圆心的分力Fn。Ft产生圆周切线方向的加速度,简称为切向加速度。切向加速度是与物体的速度方向一致的,它标志着物体速度大小的变化。Fn产生指向圆心的加速度,这就是向心加速度,它始终与速度方向垂直,其表现就是速度方向的改变。仅有向心加速度的运动是匀速圆周运动,同时具有向心加速度和切向加速度的圆周运动就是变速圆周运动。
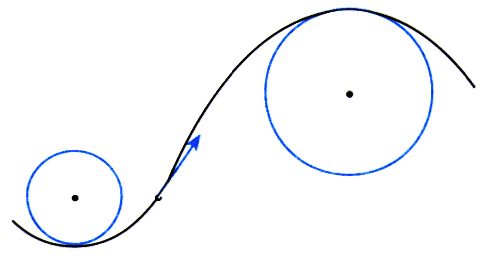
运动轨迹既不是直线也不是圆周的曲线运动,可以称为一般的曲线运动。尽管这时曲线各个位置的弯曲程度不一样,但在研究时,可以把这条曲线分割为许多很短的小段,质点在每小段的运动都可以看做圆周运动的一部分。这样,在分析质点经过曲线上某位置的运动时,就可以采用圆周运动的分析方法来处理了。
做一做
根据公式Fn=m\(\frac{{{v^2}}}{r}\) 和Fn=mω2r,物体做匀速圆周运动时,当半径比较大的时候,向心力比较大还是比较小?上节课我们曾经从理论上对向心加速度做过类似的判断,也曾以自行车为例进行讨论,现在我们再通过实验来获得体验。
如图5.6-5甲,绳子的一端拴一个小沙袋或其他小物体,绳上离小沙袋重心40 cm的地方打一个绳结A,80 cm的地方打另一个绳结B。请一位同学帮助用手表计时。
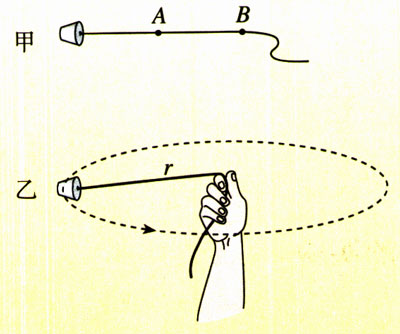
操作一 手握绳结A,如图5.6-5乙,使沙袋在水平方向做匀速圆周运动,每秒运动1周。体会此时绳子拉力的大小。
操作二 改为手握绳结B,仍使沙袋在水平方向上每秒运动1周,体会此时绳子拉力的大小。
操作三 又改为手握绳结A,但使沙袋在水平方向上每秒运动2周,体会此时绳子拉力大小。
操作二与操作一相比,沙袋的角速度相同,但它的转动半径是操作一的2倍,你感到哪次的向心力比较大?
操作三与操作二相比,沙袋的线速度相同,但它的转动半径是操作二的一半,你感到哪次的向心力比较大?
说明:因为沙袋受到重力的作用,它的运动很像圆锥摆的运动,手所提供的力不完全是向心力。但这个实验对于体会与向心力相关的因素,还是很有意义的。
问题与练习
1.地球的质量为6.0×1024 kg,地球与太阳的距离为1.5×1011m。地球绕太阳的运动可以看做匀速圆周运动。太阳对地球的引力是多少?
2.把一个小球放在玻璃漏斗中,晃动漏斗,可以使小球沿光滑的漏斗壁在某一水平面内做匀速圆周运动(图5.6-6)。小球的向心力是由什么力提供的?

3.一个圆盘在水平面内匀速转动,角速度是4 rad/s。盘面上距圆盘中心0.10 m的位置有一个质量为0.10 kg的小物体在随圆盘一起做匀速圆周运动,如图5.6-7。

(1)求小物体所受向心力的大小。
(2)关于小物体所受的向心力,甲、乙两人有不同意见:甲认为这个向心力等于圆盘对小物体的静摩擦力,指向圆心;乙认为小物体有向前运动的趋势,静摩擦力方向和相对运动趋势方向相反,即向后,而不是与运动方向垂直,因此向心力不可能是静摩擦力。你的意见是什么?说明理由。
4.如图5.6-8,细绳的一端固定于O点,另一端系一个小球,在O点的正下方钉一个钉子A,小球从一定高度摆下。经验告诉我们,当细绳与钉子相碰时,钉子的位置越靠近小球,绳就越容易断。请你利用向心力的知识解释这一现象。

5.一辆汽车在水平公路上转弯,沿曲线由M向N驶,速度逐渐减小。图5.6-9甲、乙、丙、丁分别画出了汽车转弯时所受合力F的四种方向,你认为正确的是哪个?

发布时间:2016/12/9 上午7:32:55 阅读次数:4952
