第五章 5 向心加速度

思考与讨论

我们已经知道，如果物体不受力，它将处于静止状态或做匀速直线运动。我们还知道，力的作用效果之一是改变物体的运动状态，即改变物体速度的大小或（和）方向。所以，沿着圆周运动的物体一定受力。

那么，做匀速圆周运动的物体，它所受的力沿什么方向？考虑几个实例也许会受到启发。

例1：地球绕太阳做（近似的）匀速圆周运动。地球受到什么力的作用？这个力可能沿什么方向（图5.5-1）？

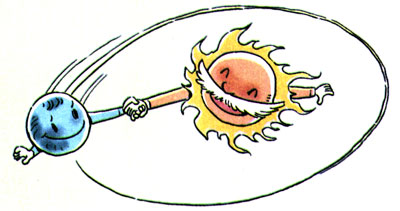
例2：光滑桌面上一个小球由于细线的牵引，绕桌面上的图钉做匀速圆周运动。小球受到几个力的作用？这几个力的合力沿什么方向（图5.5-2）？

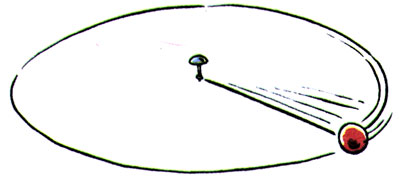
同学们还可以仿此分析几个类似的匀速圆周运动实例。

本节研究的是物体做匀速圆周运动时的加速度，分析物体的受力情况有助于了解加速度的方向。

圆周运动，即使是匀速圆周运动，由于运动方向在断改变，所以也是变速运动。既然是变速运动，就会有加速度。那么，物体的加速度指向哪个方向？在前面的实例中，物体所受的合力指向圆心，所以物体的加速度也指向圆心。

牛顿第二定律告诉我们，物体加速度的方向总与它受力的方向一致。

这个关系不仅对直线运动正确，对曲线运动同样正确。

在理论上，分析速度矢量方向的变化，可以得出普遍性的结论：任何做匀速圆周运动的物体的加速度都指向圆心。这个加速度叫做向心加速度（centripetal acceleration）。

通过进一步的分析，可以由a＝\(\frac{{\Delta v}}{{\Delta t}}\)导出向心加速度大小的表达式

a_n＝\(\frac{{{v^2}}}{r}\)

把v＝ωr代入，能够得到用角速度表示的向心加速度大小的表达式

a_n＝ω²r

做一做

探究向心加速度大小的表达式

我们尝试得出向心加速度大小的表达式，出发点是设法用v、r等物理量表示a＝\(\frac{{\Delta v}}{{\Delta t}}\)中的∆v。

在图5.5-3中，v_A、v_B是时间间隔∆t前后的速度（图甲）。为了求出二者之差∆v＝v_B－v_A，我们移动v_A，把它们的起点放在一起（图乙、图丙）。由于只有在∆t很小的时候\(\frac{{\Delta v}}{{\Delta t}}\)才表示物体的加速度，所以实际上A、B两点相距很近（图丁）。找出三角形中几个量的关系就能求得∆v。

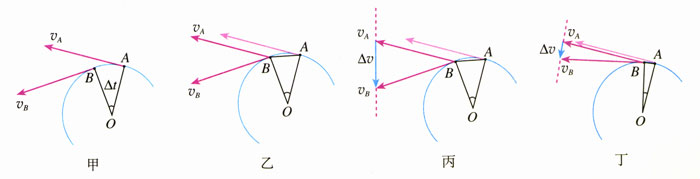
运算过程中要注意以下几点。

①于是匀速圆周运动，所以v_A和v_B的大小是一样的，可以用同一个字母v表示。

②v_A和v_B的大小实际上就是图5.5-3中v_A和v_B的长度，解决几个物理量的关系，实际是找它们的几何关系。这也是物理学中常用的研究方法。

③如图5.5-4，当角θ用弧度表示时，弧长QP可以表示为QP＝rθ。当θ很小很小时，弧长与弦长没什么区别，所以此式也表示弦长。这个关系可以用来计算矢量∆v的长度。

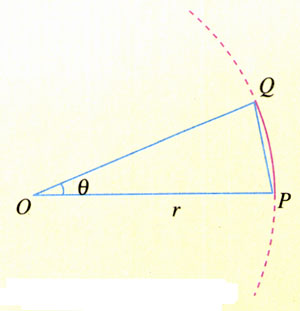
试一试！

思考与讨论

从公式a_n＝\(\frac{{{v^2}}}{r}\)看，向心加速度与圆周运动的半径成反比；从公式a_n＝ω²r看，向心加速度与半径成正比。这两个结论是否矛盾？请从以下两个角度讨论这个问题。

（1）在y＝kx这个关系式中，说y与x成正比，前提是什么？

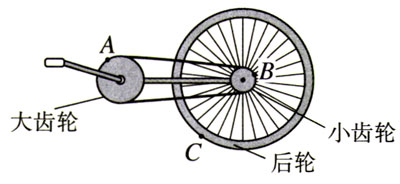
（2）自行车的大齿轮、小齿轮、后轮三个轮子的半径不一样，它们的边缘有三个点A、B、C。其中哪两点向心加速度的关系适用于“向心加速度与半径成正比”，哪两点适用于“向心加速度与半径成反比”？做出解释。

问题与练习

1．甲、乙两物体都在做匀速圆周运动，关于以下四种情况各举一个实际的例子。在这四种情况下哪个物体的向心加速度比较大？

A．它们的线速度相等，乙的半径小。

B．它们的周期相等，甲的半径大。

C．它们的角速度相等，乙的线速度小。

D．它们的线速度相等，在相同时间内甲与圆心的连线扫过的角度比乙的大。

2．月球绕地球公转的轨道接近圆，半径为3.84×10⁵ km，公转周期是27.3天。月球绕地球公转的向心加速度是多大？

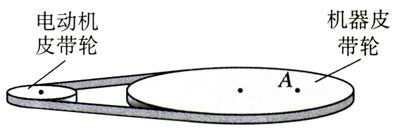
3．一部机器由电动机带动，机器上的皮带轮的半径是电动机皮带轮半径的3倍（图5.5-6），皮带与两轮之间不发生滑动。已知机器皮带轮边缘上一点的向心加速度为0.10 m/s²。

（1）电动机皮带轮与机器皮带轮的转速比n₁∶n₂是多少？

（2）机器皮带轮上A点到转轴的距离为轮半径的一半，A点的向心加速度是多少？

（3）电动机皮带轮边缘上某点的向心加速度是多少？

4．A、B两艘快艇在湖面上做匀速圆周运动，在相同的时间内，它们通过的路程之比是4∶3，运动方向改变的角度之比是3∶2，它们的向心加速度之比是多少？

发布时间：2016/12/8 上午11:05:15  阅读次数：1289