第五章 4 圆周运动
物体沿着圆周的运动是一种常见的运动。日常生活中,电风扇工作时叶片上的点、时钟指针的尖端、田径场弯道上赛跑的运动员等,都在做圆周运动。科学研究中,大到地球绕太阳的运动,小到电子绕原子核的运动,也常用圆周运动的规律来讨论。

思考与讨论
如图5.4-2,自行车的大齿轮、小齿轮、后轮是相互关联的三个转动部分。如果以自行车架为参考系,行驶时,这三个轮子上各点在做圆周运动。那么,哪些点运动得更快些?也许它们运动得一样快?

线速度
在上面的讨论中,同学们一定出现了不同意见。为什么会有不同意见?因为到目前为止,关于圆周运动,还没有大家认可的描述方法。
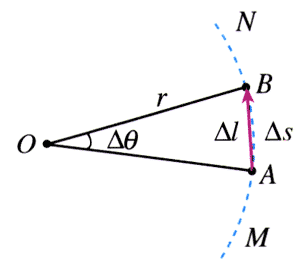
圆周运动的快慢可以用物体通过的弧长与所用时间的比值来量度。例如在图5.4-3中,物体沿圆弧由M向N运动,某时刻t经过A点。为了描述物体经过A点附近时运动的快慢,可以取一段很短的时间∆t,物体在这段时间内由A运动到B,通过的弧长为∆s。比值反映了物体运动的快慢,叫做线速度(linear velocity),用v表示,即
v=\(\frac{{\Delta s}}{{\Delta t}}\)
线速度也有平均值与瞬时值之分。如果所取的时间间隔很小很小,这样得到的就是瞬时线速度。
还有一点应该注意。当∆t足够小时,圆弧AB几乎成了直线,弧AB与线段AB几乎没有差别,此时,弧长∆s也就是物体由A到B的位移∆l。因此,这里的v实际上就是我们在直线运动中已经学过的瞬时速度,不过现在用来描述圆周运动而已。为了区别于下面将要学习的角速度,命名时在速度的前面加了一个“线”字。
线速度是矢量,图5.4-3中物体在A点的线速度的方向就是位移AB的方向。显然,当∆t很小时,这个方向与半径OA垂直,即与圆弧相切。前面曾讲到曲线运动速度的方向与轨迹相切,这里的结论是与前面一致的。
如果物体沿着圆周运动,并且线速度的大小处处相等,这种运动叫做匀速圆周运动(uniform circular motion)。应该注意的是,匀速圆周运动的线速度方向是在时刻变化的,因此它仍是一种变速运动,这里的“匀速”是指速率不变。
角速度
物体做圆周运动的快慢还可以用它与圆心连线扫过角度的快慢来描述。
如图5.4-3,物体在∆t时间内由A运动到B,半径OA在这段时间内转过的角为∆θ。它与所用时间∆t的比值,描述了物体绕圆心转动的快慢,这个比值叫做角速度(angular velocity),用符号ω表示
ω=\(\frac{{\Delta \theta }}{{\Delta t}}\)
角速度也是矢量,不过中学物理不讨论角速度方向的问题。
角速度的单位
角速度的单位由角的单位和时间的单位决定。在国际单位制中,时间的单位是秒。提到角的单位,大家自然会想到“度”,然而在国际单位制中,角的量度使用另一个单位——弧度。
如图5.4-4,圆心角θ越大,它所对的圆弧的弧长s越长,二者成正比。因此可以用弧长与半径的比值表示角的大小。例如,弧长是0.12 m,半径是0.1 m,那么
θ=\(\frac{{0.12{\rm{m}}}}{{0.1{\rm{m}}}}\)=1.2
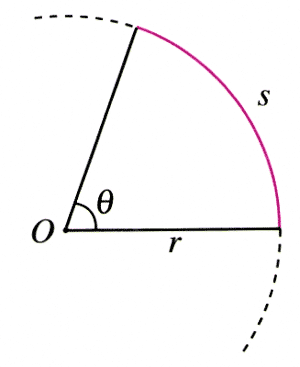
弧长与半径的单位都是米,在计算二者之比时要消掉。为了表达的方便,我们“给”θ一个单位:弧度(radian),用符号rad表示。这样,上面计算得到的角θ就是1.2弧度,记为θ=1.2 rad。
对于360º周角,用弧度表示是多少?
半径为r的整个圆周长是2πr,它与半径之比就是用弧度表示的周角
\(\frac{{2\pi r}}{r}\)=2π
即周角是2π弧度。由此推知,平角是π弧度、直角是弧度……
在用弧度表示角时,经常出现字母π。要注意,π不是单位符号,而是个数字——圆周率3.14…,所用的单位仍是弧度。
在国际单位制中以弧度量度角、以秒量度时间,所以角速度的单位是弧度每秒,符号是rad/s或s-1。
“弧度”不是通常意义上的单位,所以,带单位计算时,不要把“rad”或“弧度”写到算式中。这时角速度的单位应该写为s-1。
由于匀速圆周运动是线速度大小不变的运动,物体单位时间通过的弧长相等,所以物体在单位时间转过的角也相等。因此可以说,匀速圆周运动是角速度不变的圆周运动。
技术中常用转速来描述转动物体上质点做圆周运动的快慢。转速是指物体单位时间所转过的圈数,常用符号n表示,转速的单位为转每秒(r/s),或转每分(r/min)。
r/s和r/min都不是国际单位制中的单位,运算时往往要把它们换算成弧度每秒。
做匀速圆周运动的物体,转过一周所用的时间叫做周期(period),用T表示。周期也是常用的物理量,它的单位与时间的单位相同。思考与讨论
思考与讨论
砂轮转动时,砂轮上各个砂粒的线速度是否相等?角速度是否相等?
线速度与角速度的关系
线速度的大小描述了做圆周运动的物体通过弧长的快慢,角速度的大小描述了物体与圆心连线扫过角度的快慢。它们之间有什么关系?
在图5.4-3中,设物体做圆周运动的半径为r,由A运动到B的时间为∆t,AB弧长为∆s,AB弧对应的圆心角为∆θ。当∆θ以弧度为单位时,∆θ=\(\frac{{\Delta s}}{r}\),即
∆s=r∆θ
由于∆s=v∆t,∆θ=ω∆t,代入上式后得到
v=ωr
这表明,在圆周运动中,线速度的大小等于角速度大小与半径的乘积。
问题与练习
1.地球可以看做一个半径为6.4×103 km的球体,北京的纬度约为40º。位于赤道和位于北京的两个物体,随地球自转做匀速圆周运动的角速度各是多大?线速度各是多大?
2.某只走时准确的时钟,分针与时针由转动轴到针尖的长度之比是1.2∶1。
(1)分针与时针的角速度之比等于多少?
(2)分针针尖与时针针尖的线速度之比等于多少?
3.图5.4-5中,A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面上没有滑动。请在该装置的A、B、C三个点中选择有关的两个点,说明公式v=ωr的以下三种变量关系:
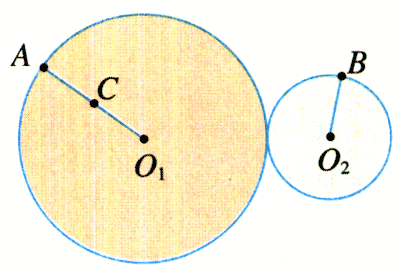
(1)v相等,ω跟r成反比;
(2)ω相等,v跟r成正比;
(3)r相等,v跟ω成正比。
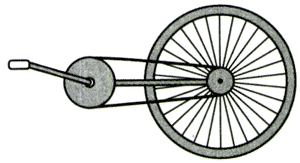
4.图5.4-6是自行车传动机构的示意图。假设脚踏板每2 s转1圈,要知道在这种情况下自行车前进的速度有多大,还需要测量哪些量?请在图中用字母标注出来,并用这些量导出自行车前进速度的表达式。
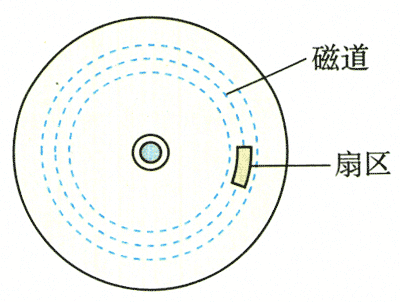
家用台式计算机上的硬磁盘的磁道和扇区如图5.4-7所示。某台计算机上的硬磁盘共有9 216个磁道(即9 216个不同半径的同心圆),每个磁道分成8 192个扇区(每扇区为\(\frac{1}{{8192}}\)圆周),每个扇区可以记录512个字节。电动机使磁盘以7 200 r/min的转速匀速转动。磁头在读、写数据时是不动的,磁盘每转一圈,磁头沿半径方向跳动一个磁道。
(1)一个扇区通过磁头所用的时间是多少?
(2)不计磁头转移磁道的时间,计算机1 s内最多可以从一个硬盘面上读取多少个字节?
发布时间:2016/12/7 下午1:18:38 阅读次数:2686
