第五章 2 平抛运动

以一定的速度将物体抛出，如果物体只受重力的作用，这时的运动叫做抛体运动（projectile motion）；抛体运动开始时的速度叫做初速度（initial velocity）。如果初速度是沿水平方向的，这个运动叫做平抛运动。以一定速度从水平桌面上滑落的物体、运动员水平扣出的排球、水平管中喷出的水流等，在空气阻力可以忽略的情况下，它们的运动都可以看做平抛运动。

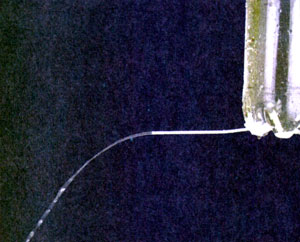
这一节我们以平抛运动为例，进一步了解研究曲线运动的方法。

平抛运动的速度

在研究直线运动时，我们已经认识到，为了得到物体的速度与时间的关系，要先分析物体受到的力，由合力求出物体的加速度，进而得到物体的速度。关于平抛运动，我们仍然遵循这样的思路，只是要在相互垂直的两个方向上分别研究。

以物体被抛出的位置为原点，以初速度v₀的方向为x轴的方向、竖直向下的方向为y轴的方向，建立平面直角坐标系（图5.2-3）。

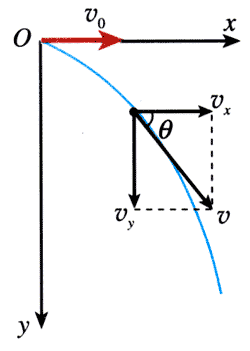
由于物体受到的重力是竖直向下的，它在x方向的分力是0，所以物体在x方向的加速度是0；又由于物体在x方向的分速度v_x在运动开始的时候是v₀，所以它将保持v₀不变，与时间t无关，即在整个运动过程中始终有

v_x＝v₀                   （1）

在y方向，由于物体受到的重力是沿着y轴的，所以重力在y方向的分力等于mg。以a表示物体在y方向的加速度，应用牛顿第二定律得到mg＝ma，由此知道a＝g，即物体在竖直方向的加速度总是等于自由落体加速度。

物体的初速度v₀沿x方向，它在y方向的分速度是0，所以物体在y方向的分速度v_y与时间t的关系是

v_y＝gt                   （2）

（2）式应用了过去的公式v_t＝v₀＋at。式中的v₀与本节的v₀并不相等。

从图5.2-3可以看出，代表速度矢量v和它的两个分矢量v_x、v_y的三个箭头正好构成一个矩形的对角线和一对邻边。由勾股定理可知

v＝\(\sqrt {v_x^2 + v_y^2} \)＝\(\sqrt {v_0^2 + {g^2}{t^2}} \)               （3）

这个式子表示，抛体在下落过程中速度v越来越大，这与日常经验是一致的。

速度的方向可以由图5.2-3中代表速度矢量秒的箭头与x轴正方向的夹角θ来表示。在这个图中，θ是一个直角三角形的锐角，它的正切等于对边与邻边之比，即

tanθ＝\(\frac{{{v_y}}}{{{v_x}}}\)＝\(\frac{{gt}}{{{v_0}}}\)            （4）

这个式子表示，速度v在抛体下落的过程中与水平方向夹角的正切越来越大。对于锐角来说，角越大，它的正切也就越大，所以（4）式告诉我们，随着抛体的下落，角θ越来越大。也就是说，抛体下落的方向越来越接近竖直向下的方向。这也与日常经验一致。

计算出tanθ的值以后，如果有需要，可以利用三角函数表或其他方法查出角θ的值。

例题1

将一个物体以10 m/s的速度从10 m的高度水平抛出，落地时它的速度方向与地面的夹角θ是多少（不讦空气阻力，取g＝10m/s²）？

【分析】按题意作图5.2-4。物体在水平方向不受力，所以加速度的水平分量为0，水平方向的分速度总等于初速度v₀＝10 m/s；在竖直方向的加速度为g，初速度的竖直分量为0，可以应用匀变速运动的规律求出竖直方向的分速度。

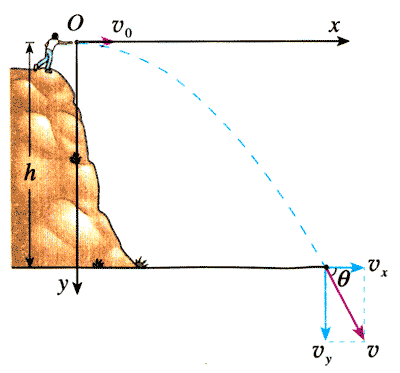
【解】以抛出时物体的位置为原点建立直角坐标系，x轴沿初速度方向，y轴竖直向下。

落地时，物体在水平方向的分速度是

v_x＝v₀＝10 m/s

根据匀变速运动的规律，落地时物体在竖直方向的分速度v_y满足以下关系

v_y²－0＝2gh

由此解出

v_y＝\(\sqrt {2gh} \)＝\(\sqrt {2 \times 10 \times 10} \)m/s＝14.1m/s

tanθ＝\(\frac{{{v_y}}}{{{v_x}}}\)＝\(\frac{{14.1}}{{10}}\)＝1.41

通过查找数学用表或其他方法找到与1.41最接近的正切值，得到与之对应的角

θ＝55°。

物体落地时速度与地面的夹角是55°。

平抛运动的位移

物体被抛出后，它对于抛出点O的位移l（图5.1-1）的大小、方向都在变化。这种情况下我们就要分别研究它在两个坐标轴上的分位移x和y。通过前面的讨论我们已经知道平抛运动中v_x＝v₀，这意味着，假如一个物体在沿x轴以恒定的速度v₀运动，它的运动规律就代表了做平抛运动的物体在x方向的分位移的变化规律。这个规律正是匀速运动的规律。根据匀速运动的位移与时间的关系，我们得知，做平抛运动的物体的横坐标与时间的关系是

x＝v₀t                   （5）

此相似，假如一个物体在沿y轴以v_y＝gt的规律运动，它的运动规律就代表了做平抛运动的物体在y方向的分位移的变化规律，而v_y＝gt正表示一个质点从静止开始在以加速度g做匀加速运动。根据匀加速运动的知识，可知做平抛运动的物体的纵坐标与时间的关系是

y＝\(\frac{1}{2}\)gt²               （6）

如果需要知道物体对于抛出点的位移，应该怎样计算？

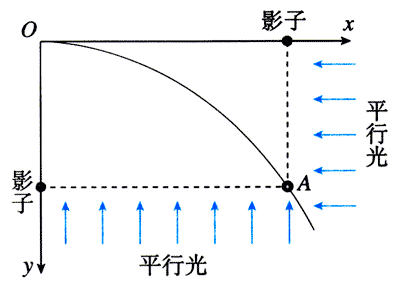
（1）（2）（5）（6）几个式子描述了做平抛运动的物体的运动规律。我们可以形象地说明它们与这个物体的运动的关系。如图5.2-5，两束光分别沿着与坐标轴平行的方向照射物体A，在两个坐标轴上留下了物体的两个“影子”。“影子”的位移和速度描述了物体A在x、y两个方向的运动。

做一做

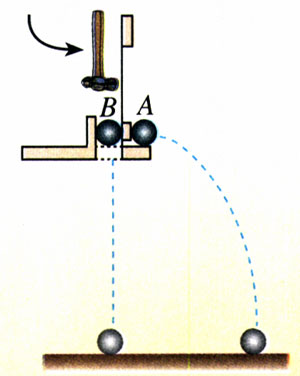
如图5.2-6，用小锤打击弹性金属片后，A球沿水平方向抛出，同时B球被松开，自由下落。A、B两球同时开始运动。

观察两球哪个先落地。

改变小球距地面的高度和打击的力度，重复这个实验。

实验现象说明了什么问题？

实验时，也可以用耳朵“听”来判断两球落地时刻的先后。

例题2

从本节（5）（6）两式出发，讨论做平抛运动的物体的运动轨迹。

【分析】根据初中学过的数学知识，一条平面曲线可以用x、y之间的一个关系式来描述。例如，y＝kx＋b代表一条直线、y＝ax²＋bx＋c代表一条抛物线（图5.2-7）。因此，要想知道物体被抛出后沿着什么样的曲线运动，也就是要想知道物体的运动轨迹，就要知道描述物体位置的两个变量x、y之间的关系式。

式中k、a、b、c都是与x、y无关的常量。

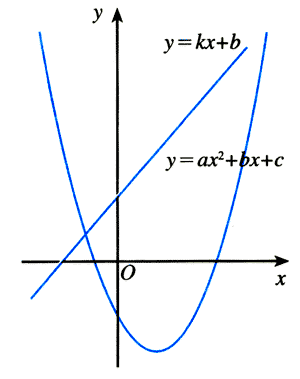
本节（5）（6）两式给出了x、y的表达式，如果从中消去时间t，就能得到所需的x、y之间的关系式了。

【解】从（5）式解出t＝\(\frac{x}{{{v_0}}}\)，代入（6）式，得到

y＝\(\frac{g}{{2v_0^2}}\)x²             （7）

在这个式子中，自由落体加速度g、抛体的初速度v₀都是不随时间变化的常量，\(\frac{g}{{2v_0^2}}\)也就是说，这个量与x、y无关，因此（7）式具有y＝ax²的形式。根据初中数学知识我们得知，它代表一条抛物线。

平抛运动的轨迹是一条抛物线（parabola）。数学中把二次函数的图线叫做抛物线，这个名称就是由抛体运动得来的。

一般的抛体运动

如果物体被抛出时的速度v₀不沿水平方向，而是斜向问上方或斜向下方（这种情况常称为斜抛），它的受力情况与平抛运动完全相同：在水平方向不受力，加速度是0；在竖直方向只受重力，加速度是g。

但是，斜抛运动沿水平方向和竖直方向的初速度与平抛不同，分别是v_x＝v₀cosθ和v_y＝v₀sinθ。仿照平抛运动的处理方法也能得到描述斜抛物体运动的几个关系式。图5.2-8甲是根据这一规律描绘出的斜抛运动的轨迹。

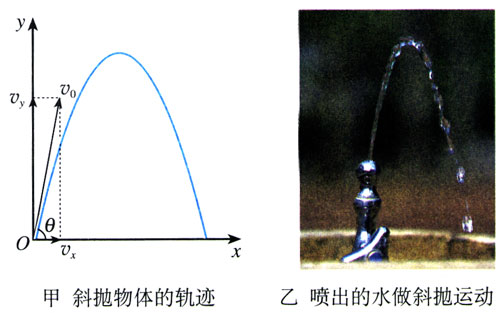
说一说

1．尝试导出表达图5.2-8甲所示斜抛物体运动轨迹的关系式。讨论这个关系式中物理量之间的关系，看看能够得出哪些结论。

2．以上讨论都有一个前提，即空气的阻力可以忽略。如果速度不大，例如用手抛出一个石块，这样处理的误差不大。但是物体在空气中运动时，速度越大，阻力也越大，所以，研究炮弹的运动时就不能忽略空气的阻力。根据你的推测，炮弹运动的实际轨迹大致是怎样的？

问题与练习

1．一条水平放置的水管，横截面积S＝2.0 cm²，距地面高h＝1.8 m。水从管口以不变的速度源源不断地沿水平方向射出，水落地的位置到管口的水平距离是0.9 m。

问：每秒内从管口流出的水有多大体积？计算时设管口横截面上各处水的速度都相同，自由落体加速度取g＝10 m/s²，不计空气阻力。

2．某卡车在限速60 km/h的公路上与路旁障碍物相撞。处理事故的警察在泥地中发现了一个小的金属物体，可以判断，它是事故发生时车顶上一个松脱的零件被抛出而陷在泥里的。警察测得这个零件在事故发生时的原位置与陷落点的水平距离为13.3 m，车顶距泥地的竖直高度为2.45 m。请你根据这些数据为该车是否超速提供证据。

3．如图5.2-9，在水平桌面上用练习本做成一个斜面，使小钢球从斜面上某一位置滚下，钢球沿桌面飞出后做平抛运动。

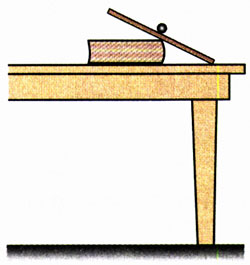
怎样用一把刻度尺测量钢珠在水平桌面上运动的速度？说出测量步骤，写出用所测的物理量表达速度的计算式。

4．某个质量为m的物体在从静止开始下落的过程中，除了重力之外还受到水平方向的大小、方向都不变的力F的作用。

（1）求它在时刻t的水平分速度和竖直分速度。

（2）建立适当的坐标系，写出这个坐标系中代表物体运动轨迹的x、y之间的关系式。这个物体在沿什么样的轨迹运动？

发布时间：2016/12/5 下午3:16:08  阅读次数：4539