第7章 八、振动中的能量转化 *共振

振动中的能量转化

弹簧振子和单摆，在振动过程中，速度的大小时刻在变化，由于弹簧振子和摆球都具有一定的质量，它们的动能也就时刻变化。那么，它们的能量是怎样转化的呢？我们以弹簧振子的振动为例进行分析。

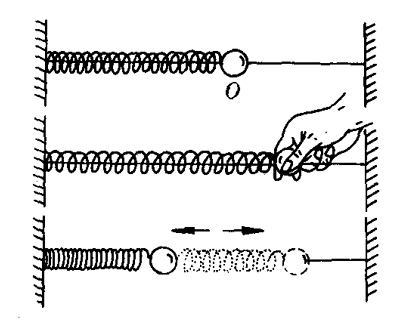
把振子从平衡位置O拉开一段距离的过程中（图7-50），由于外力克服弹力做功，弹簧振子的弹性势能增大。放开后，振子从最大位移处向平衡位置运动的过程中，由于弹力做功，弹性势能逐渐减小，转化为振子的动能。当振子到达平衡位置时，弹性势能减小为零，振子动能变得最大。振子从平衡位置向另一侧的最大位移处运动的过程中，振子克服弹力做功，弹性势能不断增大，振子动能不断减小。当振子到达另一侧最大位移处时，动能减小到零，弹性势能最大。接着，振子重又向平衡位置运动，弹性势能又逐渐转化为动能。

思考

单摆在振动过程中，能量是如何转化的？

固有振动 受迫振动

任何物体都具有一定的固有频率（或固有周期），物体以它的固有频率作振动，叫做固有振动。在日常生活和生产中还可见到一类振动，例如人们坐在发动机正在工作的车、船中，会感到座位由于机器运转引起的振动；建筑工人使用风镐时，身体可产生明显振动。这类振动是在周期性外力作用下发生的，它们的共同特点是，物体振动的频率跟周期性外力的频率总是相等的。

物体在周期性外力作用下的振动，叫做受迫振动。若把这种周期性的外力叫做策动力，那么，就可以说物体做受追振动的频率等于策动力的频率，而跟物体的固有频率无关。

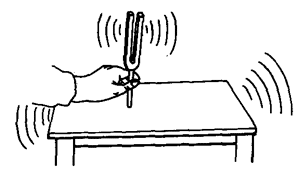
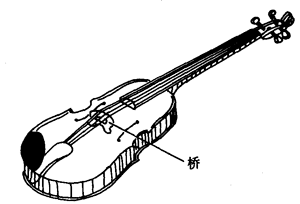
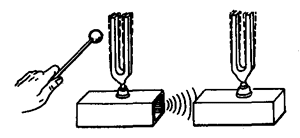
我们可用以下实验来说明。用橡皮槌敲击一下音叉，音叉就产生振动，发出一定音调的声音。如把这个振动着的音叉的柄紧压在桌面上，就可听到同一音调、响度明显增大的声音。这是由于音叉振动对桌面产生策动力，桌面就做受迫振动而发声（图7-51）。听到的桌面发声和音叉发声的音调相同，说明受迫振动的频率等于策动力的频率。如换另一频率的音叉再做实验，桌面就以这另一频率做受迫振动而发声。各种弦乐器，如提琴、胡琴等就是通过“桥”和音柱（图7-52），把弦的振动传给音箱，使音箱（包括内部空气）做受迫振动而发声。

阻尼振动和无阻尼振动

由于摩擦和介质阻力的存在，弹簧振子和单摆在振动过程中，不断克服外界阻力做功而消耗能量，振幅就会逐渐减小，经过一段时间，振幅减小到零，振动完全停止。

振幅随时间逐渐减小的振动，叫做阻尼振动。阻尼振位移动是一种减幅振动[图7-53（a）]。阻尼振动在生活中和自然界中都是常见的。物体作阻尼振动时，振幅减小的快慢程度跟振动体周围的介质性质有关。若介质阻力很大，振动很快减弱。如单摆在空气中可以振动较长时间，若放入水中，就会很快停止振动。

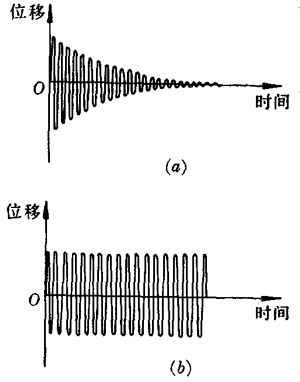
如果在振动过程中，适时地给振动系统补充一定的能量，以弥补克服阻力做功所消耗的能量。这样，就可以使振动的振幅不再减小，这种等幅振动也可以看作是无阻尼振动[图7-53（b）]。

*共振

如图7-54所示，将一块薄木片的一端用桌夹固定在桌边，在木片的另一端固定一个带有偏心装置的玩具电动机，用手拨动木片，可以观察到木片连同电动机，以它自身的固有频率作振动。

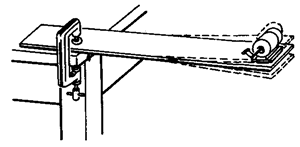
玩具电动机连接电源后，由于偏心作用，电动机转动时对木片有周期性的外力作用，木片做受迫振动。若电动机转速很大，产生的策动力频率远大于木片连同电动机这一装置的固有频率时，可以看到木片做受迫振动的振幅很小。利用滑动变阻器改变电动机两端电压，使电动机转速连续可调。这样，当电动机转速逐渐变小，策动力频率逐渐接近这一装置的固有频率时，可以看到木片的振幅逐渐增大。而当策动力频率等于这一装置的固有频率时，木片的振幅变得很大。继续减小电动机转速，当策动力频率小于这一装置的固有频率时，可以看到木片的振幅又变小了。图7-55的曲线表示物体做受迫振动时的振幅跟策动力频率的关系。

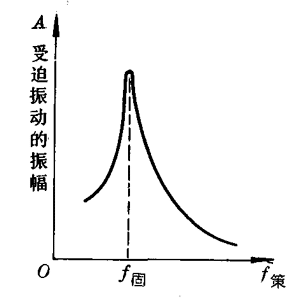
物体做受迫振动时，当策动力频率跟物体的固有频率接近时，物体的振幅急剧增大；当策动力频率跟物体的固有频率相等时，物体的振幅达到最大，这种现象叫做共振（resonance）。共振现象是受迫振动的特例。

*共振在技术上的意义

共振现象有很多应用。例如，音叉共鸣箱就是一个典型例子。把某一频率的音叉插在一定长度的一端开口的共呜箱上，当敲击音叉使它振动时，箱内的空气柱就能产生共振，发出较响的声音，叫做共鸣。共鸣是一种声共振现象。

如果把两个相同频率的音又及其共鸣箱，如图7-56所示放置。敲击其中一个音叉，过了几秒钟，用手握住该音叉的股叉，不使它振动，这时可以听到另一个音叉发出的轻微的声音。这是因为第一个音叉振动时产生的声音频率，和第二个音又及其共鸣箱中空气柱的固有频率相同，第二个共鸣箱内空气柱和音叉产生共振而发声。

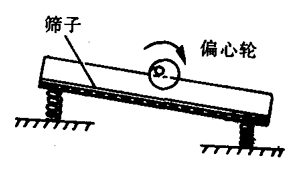
共振筛（图7-57）是一种利用共振原理的机械，把筛子用4根弹簧支承起来，就成为共振筛。共振筛的筛架上安装一个偏心轮，偏心轮上另装有皮带轮，与动力相连。皮带轮带动偏心轮转动时，筛子就受到一个周期性的策动力作用而做受迫振动。调整偏心轮的转速，使策动力的频率接近共振筛的固有频率，筛子就发生共振，达到较大的振幅，提高了筛除杂物的效率。

课本彩图18是我国古代鱼洗的复制品。鱼洗是一个带耳环的铜盆，盆底有浮雕的鱼，在盆内注入适量的水，用手同时摩擦铜盆的两个耳环，只要摩擦引起的策动力频率和铜盆（连同水）的固有频率接近时，铜盆就发生共振，盆内的水飞溅出来，盆底浮雕的鱼也好像活了起来要跃出水面一般。鱼洗是我国古代劳动人民智慧的结晶。

在有些情况下，共振现象会造成严重后果，必须设法防止。例如，规定部队经过桥梁时一律要改用便步行走，这样，才不会对整座桥梁形成周期性外力，以免桥梁发生共振。本世纪60年代，美国某空军基地附近，一架军用喷气飞机低空掠过一批相同结构的民房时，由于喷气发动机产生的脉冲气流形成的策动力频率，接近这种建筑物的固有频率，致使数十幢民房发生共振而倒坍，以后有关部门就规定喷气飞机不得在有建筑物的地方超低空飞行。轮船航行时，会受到周期住的海浪冲击而左右摇摆。如果海浪冲击力的频率跟轮船摇摆的固有频率相同，就会发生共振，造成轮船倾覆事故。若改变轮船的航向和速率，就能使海浪冲击力的频率远离轮船的固有频率。冲床等机器在工作时会产生周期性的策动力，为了避免损坏机器本身和安装这类机器的厂房，在设计机器、建筑厂房时，应使它们的固有频率尽可能远离机器运转产生的策动力频率。

人在生活和生产中会接触到各种振动源。由科学测试知道人体各部位有不同的固有频率，如眼球的固有频率最大约为60赫，颅骨的固有频率最大约为200赫等；把人作为一个整体来看，水平方向的固有频率约为3赫～6赫，竖直方向的固有频率约为4赫～8赫。因此，跟振动源十分接近的操作人员，如拖拉机驾驶员，风镐、风铲、电锯、铆钉机等操作工，要保证这些振动源的策动频率远离人体有关部位的固有频率。为了保障工人的安全与健康，医疗保健部门作出了有关规定，如规定用手操作的各类振动机械的频率必须大于20赫。

总之，在需要利用共振的时候，应使策动力频率接近或等于振动物体的固有频率。在需要防止共振产生的危害时，要设法使策动力频率远离振动物体的固有频率。

思考

1．缝纫机工作时，缝针上、下振动，这是缝针的固有振动还是受迫振动？

*2．登山运动员在雪线以上攀登时，不准大声呼喊，也不准鸣枪，因为那样做，可能会引起雪崩，这是什么道理？

*3．跳水运动员在跳板跳水训练时，用脚蹬踏跳板的频率应远离跳板的固有频率，还是应接近跳板的固有频率？

本章学习要求

1．知道周期运动的特点。知道周期。

2．理解匀速圆周运动。理解匀速圆周运动的周期。

3．理解匀速圆周运动的线速度。理解线速度和周期的关系。

4．理解匀速圆周运动的角速度。理解线速度和角速度的关系。

5．理解线速度、角速度和周期之间的关系。

6．理解向心力。理解向心加速度。

7．理解万有引力定律。

8．常识性了解人造地球卫星。

9．常识性了解第一宇宙速度。

10．知道机械振动。

11．知道简谐振动的产生条件和特征。

12．知道振动的振幅。理解振动的周期和频率以及它们之间的关系。

13．知道振动图象。

14．知道单摆作简谐振动的条件。知道单摆振动的规律和理解单摆周期公式。

15．会利用单摆测重力如速度。

16．知道振动过程中能量的转化。

17．知道固有振动。知道受迫振动。

复习题

1．单选题：

（1）在图7-58所示的摩擦传动装置中，主动轮A的半径是r₁，从动轮B的半径是r₂，主动轮的轮缘压紧在离从动轮轴心O的距离为\(\frac{2}{3}\)r₂处。已知A.B两轮的半径比r₁∶r₂＝1∶3，则A、B两轮轮子边缘质点的向心加速度之比是（    ）

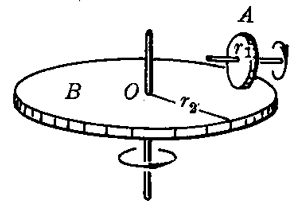
（A）3∶1；        （B）1∶3；        （C）2∶3；        （D）4∶3。

（2）某种压路机，前面的导向轮半径较小，后面驱动轮半径较大（图7-59）。正常行驶时，它的前、后轮边缘质点A和B相对于前、后轮的轴做匀速圆周运动。如果前、后轮的半径之比为2∶3，则A、B质点的线速度v的大小和周期T的大小关系是（    ）

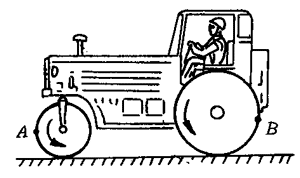
（A）\(\frac{{{v_{\rm{A}}}}}{{{v_{\rm{B}}}}}\)＝\(\frac{2}{3}\)；\(\frac{{{T_{\rm{A}}}}}{{{T_{\rm{B}}}}}\)＝1             （B）\(\frac{{{v_{\rm{A}}}}}{{{v_{\rm{B}}}}}\)＝\(\frac{3}{2}\)；\(\frac{{{T_{\rm{A}}}}}{{{T_{\rm{B}}}}}\)＝\(\frac{2}{3}\)

（C）\(\frac{{{v_{\rm{A}}}}}{{{v_{\rm{B}}}}}\)＝1；\(\frac{{{T_{\rm{A}}}}}{{{T_{\rm{B}}}}}\)＝\(\frac{2}{3}\)              （D）\(\frac{{{v_{\rm{A}}}}}{{{v_{\rm{B}}}}}\)＝1；\(\frac{{{T_{\rm{A}}}}}{{{T_{\rm{B}}}}}\)＝\(\frac{3}{2}\)

（3）一座在海平面上校准的摆钟，移到高原地区使用时不准了，要使它走时准确，可能采取的调节方法是（  ）

（A）增长摆长；               （B）缩短摆长；

（C）增大摆锤质量；        （D）减小摆锤质量。

（4）在同一地点有甲、乙两个单摆。当甲摆振动120次时，乙摆恰好振动了80次。则甲、乙两摆的摆长之比是（    ）

（A）3∶2；        （B）2∶3；        （C）9∶4；        （D）4∶9。

2．一根长0.5米的细线，能够承受的最大拉力是10牛。现把这根细线的一端固定，另一端拴一个质量为200克的小球，使它在光滑的水平桌面上做匀速圆周运动，那么小球的线速度最大不能超过多少？

3．混凝土搅拌车上的料斗在不停地匀速转动，如果每转一圈需80秒，料斗直径最大处为2米，则其中混凝土拌料的最大向心加速度多大？

4．观看宇航员在月球表面从事科学考察活动的电视录像时，在一组镜头中看到宇航员手中拿着一个带有长柄的土壤收集器，跟他的身高相比较，估计这一器具的长度约为1米（图7-60）。当他收集满了土壤，提起长柄收集器时，收集器发生了轻微晃动，从电视画面上估计晃动的周期约为5秒。根据这些估计数据，并且粗略地把长柄土壤收集器的晃动当作单摆振动处理，你能否估算出月球表面重力加速度的大小？

5．世界各国发射的人造地球卫星的运行周期都大于90分，能否发射一个沿圆轨道运行、周期只有1小时的人造地球卫星？已知第一宇宙速度为7.9×10³米/秒。

6．月球质量为7.35×10²²千克，半径为1738千米。试计算从月球表面发射的人造月球卫星的最小周期。

7．一个单摆，当它的摆长增加副0.8米时，它的周期增大为原来的4/3倍，试求单摆原来的摆长和周期。

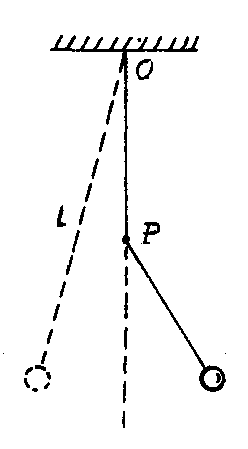
8．在摆长为l的单摆悬点以下l/2的地方，固定一个钉子P（图7-61）。当单摆自左向右振动到平衡位置时，由于钉子的阻碍，它在另一侧的摆动情况将发生改变。如果单摆在另一侧的振动仍可看成简谐振动，试求这一单摆的振动周期。

发布时间：2016/12/1 上午7:00:55  阅读次数：2607