第7章 五、行星的运动
远古时代的人们,就已注意到日月星辰等天体的运动具有周期性。“日出而作,日落而息”就是根据太阳和地球间的相对运动而使人们自然形成的生活节奏。但究竟是“天动”还是“地动”,在历史上曾经有过长期的争论。
公元2世纪,古希腊天文学家托勒玫(约90—168)综合了许多天文学家的观测资料,提出了地心说,认为不动的地球是宇宙的中心。这种观点是基于从地球上观察天体位置的变化,以为所有天体都围绕地球转动,这与当时教会认为“地球是上帝的宝座”的观点相吻合。“天动”的观点一直持续了1000多年。到了16世纪,随着航海事业的发展,各种观测手段的日益完善,积累资料的日益丰富,人们逐渐发现地心说与实际观测的结果有越来越大的矛盾。波兰天文学家哥白尼(1473—1543)于1543年发表了《天体运行论》,提出与地心说完全相对立的曰心说,认为地球和其他行星都是环绕太阳运行的,太阳是宇宙的中心,并明确指出人们观察到的太阳东升西落是由于地球自转所引起的。《天体运行论》以大量的观测事实为根据,以严密的数学运算来论证日心说的观点,并准确预言月食和当时已知的行星的位置,使自然科学摆脱了神学的束缚。
行星的运动
宇宙太空有无数运动着的天体,它们形成了不同层次的天体系统。月球绕地球公转构成了地月系;地球和其他绕太阳公转的行星、彗星等构成了太阳系;约有2000多亿个像太阳系那样的恒星系构成了银河系;银河系以外、类似银河系的星系叫做河外星系(图7-27)。银河系和观察到的10亿多个河外星系构成了总星系。在这众多的天体系统中,跟人类的生活和生产关系最为密切的是太阳系和地月系。人们很早就对行星的运动和月球的运动进行了观察研究。由于行星绕太阳的运动和月球绕地球的运动是周期运动,人们才有可能一代接一代地对它们的运动进行无数次的重复观察。

图7-27
17世纪初,德国天文学家开普勒(1571-1630)在哥白尼日心说的基础上,根据丹麦天文学家第谷(1546-1601)留下的大量天体观测资料,先后用了17年时间,对当时已经发现的6个行星绕日运动的轨道和规律进行反复计算和观测,指出各个行星绕日运动的轨道是一系列大小不同的椭圆轨道,太阳是在这些椭圆的一个焦点上(图7-28)。各个行星的绕日运动都是周期运动,离太阳最近的水星的绕日运动周期最小,约是地球的1/4;离太阳最远的土星的绕日运动周期最大,约是地球的29倍。
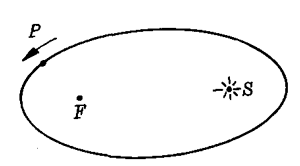
开普勒得出的行星运动觌律,不仅适用于行星绕太阳的运动,同样也适用于卫星绕行星的运动。
思考
我国于1970年4月24日发射第一颗人造地球卫星,它的近地点是439千米,远地点是2384千米。这些数据表示,这颗人造地球卫星的轨道是什么形状?地球位于这一轨道的什么位置?
万有引力定律
天文观测表明,金星、地球等行星的绕日运动都是沿着各自的近似于圆的轨道进行,可以看成是作匀速圆周运动,它必定受到指向太阳的向心力作用,这一向心力只能是太阳对行星的引力。牛顿经过严密论证后确认,使物体加速落向地面的力和太阳使行星保持在它们轨道上运动的力是同一性质的力,宇宙中任何有质量的物体之间都存在着相互吸引的力,牛顿把这种力叫做万有引力。
研究表明,两个物体间的引力大小,跟物体的质量的乘积成正比,跟它们间的距离的平方成反比。这就是万有引力定律。
万有引力定律可用下式表示
F=G\(\frac{{{m_1}{m_2}}}{{{r^2}}}\),
式中F表示万有引力,m1、m2表示两个物体的质量,r表示两物体间的距离,比例常数G叫做万有引力恒量。
我国法定计量单位中,力F的单位是牛,距离r的单位是米,质量m的单位是千克,由实验测定的万有引力恒量G=6.67×10-11牛·米2/千克2。它表示两个质量各为1千克的物体相距1米时,它们之间的万有引力等于6.67×10-11牛。
万有引力定律的发现,是17世纪自然科学最伟大的成果之一,这一定律把地面附近物体下落运动的受力规律与天体运动的受力规律统一起来,它第一次揭示了存在于自然界中的一种基本的相互作用——引力的规律,这对以后物理学和天文学的发展有着深远的影响。
思考
1.既然一切物体间都存在万有引力,那么,教室里的桌椅等物品为什么都没有被吸引在一起?
2.如果地球突然失去太阳的引力作用将会怎样?如果地球失去绕日运动的速度,结果又将怎样?
3.甲物体的质量是乙物体质量的4倍,所以甲物体对乙物体的引力应是乙物体对甲物体引力的4倍,这样的说法正确吗?为什么?
4.当两物体间的距离增大为原来的4倍时,两物体间的万有引力将减小为原来的1/4,这样的说法正确吗?为什么?
*卡文迪许实验
牛顿发现了万有引力定律,能很好地解释天体的运动,但当时由于受到实验仪器精确程度的限制,在实验室中无法检验万有引力定律和测出万有引力恒量G的数值。直到1798年,即在牛顿发现万有引力定律100多年后,英国科学家卡文迪许(1731-1810)利用扭秤这一巧妙的实验装置,才解决了这一个难题。
图7-29是卡文迪许设计的扭秤装置示意图。在一根轻杆的两端分别固定两个质量相等的小铅球,用一根细石英丝挂住轻杆,使轻杆保持水平,石英丝上装有一块小平面镜,它能把经过狭缝射来的一细束光,反射到刻度标尺上的某一个位置。两个质量相等的大铅球固定地放在如图中所示的位置,它们跟小铅球的距离相等。由于万有引力的作用,两个小球便向大球靠近,两个小球的运动使石英丝发生扭转,石英丝的扭转角度可以从平面镜的反射光束在刻度尺上移动的距离求出。根据扭转角度,可以推算出大、小球间万有引力F的大小。已知大、小铅球的质量m1、m2和测出两球间的距离r,便可计算出万有引力恒量G的数值。
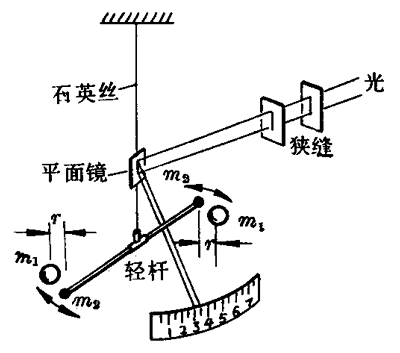
卡文迪许实验证实了万有引力定律的正确性,测出了万有引力恒量。他当时测定的结果跟现代公认的G值很接近。
人造地球卫星
我们已经知道,由于地球引力的存在,抛出的物体总要落回地面。生活经验又告诉人们,抛出物的速度大些,它就可以飞行一段较长的距离才落回地面。那么,是否有可能使物体具有足够大的速度而再也不会落回地面呢?牛顿在他的著作中有一幅原理图(图7-30)回答了这个问题。牛顿认为如果从山顶上水平抛出一个物体,速度较小时,物体将落在山脚下附近的A处;若抛出速度逐渐增大,则物体的落地点依次为B、C、D等处;如果速度大到使它永远不会落回地面,那么,这个物体将环绕地球表面做圆周运动,成为一个人造地球卫星。
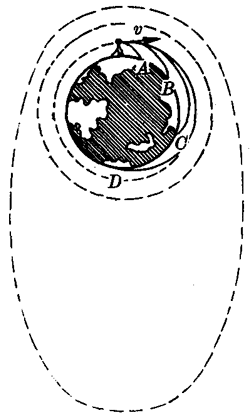
计算人造卫星的速度需要运用万有引力定律和向心力公式。卫星环绕地球做圆周运动所需的向心力就是地球对它的引力。假设卫星的质量为m,速度为v,运动半径(差不多等于地球的半径)为R,地球的质量为M,于是
G\(\frac{{Mm}}{{{R^2}}}\)=\(\frac{{m{v^2}}}{R}\),
得到 v=\(\sqrt {\frac{{GM}}{R}} \)。
上式表明,v的大小决定于地球的质量和半径,而跟卫星质量大小无关。人们把这个速度叫做第一宇宙速度,又称环绕速度。将地球质量M=5.98×1024千克,地球半径R=6.4×106米,万有引力恒量G=6.67×10-11牛·米2/千克2代入上式,可计算出第一宇宙速度v1=7.9×103米/秒。但在牛顿的时代,无法使物体获得如此大的速度,直到本世纪火箭发动机的发明和多级火箭技术的发展,才有可能实现人类这一理想。
1957年10月,前苏联率先发射人造地球卫星获得成功。1970年4月,我国成功地发射了“东方红”人造地球卫星。20多年来,我国已先后发射了30多颗用于各种不同用途的人造地球卫星(图7-31)。

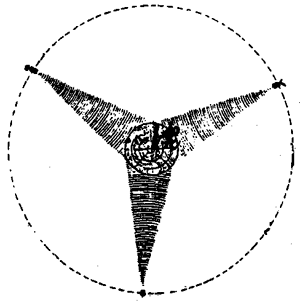
目前世界上已有十几个国家先后发射了各种人造地球卫星,地球外层空间的人造天体(包括人造卫星和空间站)总数已达数千个。人造地球卫星上装备各种不同的科学仪器,就可达到科学探测、微波通信、军事侦察、资源调查、气象顶报、环境监测、控制污染、估计农作物收成、发现病虫害灾情等目的。采用发射到地球赤道上空同步轨道上互成120°角的三颗同步卫星(又称通信卫星)(图7-32),就可以实现全球的电视转播。同步卫星环绕地球运动一周的时间和地球自转的周期相等,也就是说它在赤道上方跟地面保持相对静止,犹如悬在空中一样(课本彩图15)。理论计算表明,同步卫星离地面的高度为3.58×107米,约为地球半径的6倍。同步卫星在轨道上的运行速度是个定值,大约为3.1×103米/秒。

*航天技术的发展
自从1883年,俄国齐奥尔科夫斯基发表了使用火箭发射太空船的构想以来,一个多世纪过去了。近几十年来,世界各国对太空开发的理论研究和实践有了突飞猛进的发展。
航天活动的主要目的是探索、开发和利用太空以及地球以外的天体。航天包括环绕地球的运行,飞往月球或其他行星的航行。1961年4月,前苏联成功地发射了“东方一号”载人太空飞船,由加加林驾驶的飞船环绕地球一周后,顺利返回地面,实现了世界上第一次太空飞船的载人飞行。美国从1967年起,开始执行宏伟的“阿波罗”计划,经历了多次失败,多名宇航员为此献出了生命,终于在1969年7月16日成功地发射了“阿波罗11号”,它穿越3.844×108米遥远的太空,于7月21日到达月球表面。美国宇航员阿姆斯特朗作为人类的代表第一次踏上了月球(图7-33),宣告了人类的活动不再局限于地球。

20年来,我国的航天事业也有了迅速发展。继1970年我国发射第一颗人造卫星后,从1975年起,我国就掌握了使卫星返回地面的回收技术。1981年9月,我国成功地用一枚运载火箭将3颗空间物理探测卫星送入轨道。1982年10月,我国成功地试验了从水下潜射火箭,这对巩固国防具有重要意义。1984年4月8日,我国成功地发射了一颗同步定点试验通信卫星,这样,我国就成为少数几个能独立发射同步卫星的国家之一。1986年2月1日又发射成功一颗实用广播通信卫星。目前,我国的运载火箭和卫星技术已从探索试验阶段发展到实用阶段,且已跨入世界先进行列。1995年4月北京空间技术实验中心的奠基,预示着我国宇航员培训的开始。
第二宇宙速度和第三宇宙速度
理论计算表明,如果人造地球卫星进入轨道时的水平速度大于7.9×103米/秒而小于11.2×103米/秒,它绕地球运动的轨道就不是圆而是椭圆(图7-34)。当卫星的速度等于或大于11.2×103米/秒时,卫星就能挣脱地球引力的束缚,成为绕太阳运动的人造行星。前苏联在1959年1月发射的准备探测月球背面情况的人造卫星“月球1号”,它沿着一个很扁的椭圆轨道运行,轨道的远地点在月球背后。但因速度大于11.2×103米/秒,它就成了一颗绕太阳运行的人造行星,再也不会接近地球。11.2×103米/秒这个速度叫做第二宇宙速度,也叫做脱离速度。
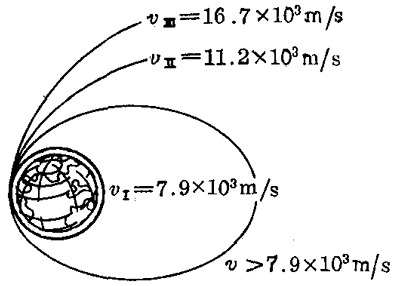
达到第二宇宙速度的物体脱离地球后还受到太阳引力的束缚。要想使物体挣脱太阳引力的束缚,飞到太阳系以外的宇宙空间去,必须使它的速度等于或大于16.7×103米/秒。这个速度叫做第三宇宙速度,也叫做逃逸速度。
上述的第一、第二和第三宇宙速度的数值都是对地球而言的,其他行星包括行星的卫星也都有它们各自的宇宙速度。以月球为例,因为它的质量和半径都比地球小,所以在月球表面发射人造月球卫星只需要较小的速度,登月舱的上升级从月球表面返回指令舱时,所消牦的能量比脱离地球表面时小得多(图7-35)。

练习三十六
1.质量不同的两个物体,它们受到的地球引力的大小是( )
(A)一定相等; (B)一定不相等;
(C)质量大的物体受到的地球引力大; (D)条件不够,无法判断。
2.两个质量均为3.2千克的铅球,放在操场上相距2米,试求它们之间的万有引力。
3.在地面受重力为1.058×103牛的实验装备,用火箭送上离地面2.6×106米高度时,这些装备受到的地球引力将变为多大?
4.贴近地球表面运行的人造地球卫星的周期多大?已知地球半径为6.4×103千米。
5.月球质量约是地球质量的1/81,月球半径约是地球半径的1/3.7,地球的第一宇宙速度是7.9×103米/秒。从月球表面发射人造月球卫星至少需要多大的速度?
阅读材料
太空探测的新时代
从本世纪60年代开始,前苏联、美国先后发射了各类空间站和行星探测器,执行长期的科学考察任务(课本彩图17)。进入80年代后,1981年美国研制的一种可以重返大气层、多次使用的航天飞机试飞成功(课本彩图16)。航天飞机除了能进行科学考察外,还可在空间发射和回收卫星(图7-36)。



1989年5月5日,美国“麦哲伦号”金星探测器由美国“阿特兰蒂斯号”航天飞机进入大空后6小时发射。这一探测器于1990年8月10日到达金星上空,进入绕金星运行的椭圆轨道,成为周期是3.15小时的金星的一颗人造卫星。它将拍摄到的金星表面图象发回地球。“麦哲伦号”探测器的考察揭示了金星的起源和演化过程,从而有助于研究和了解地球的起源和演化。今后行星际探测将进一步扩展到其他行星,还将研究恒星、类星体和宇宙的起源。
目前世界各国航天技术的发展,围绕着以下两方面进行。在无人航天器方面,进一步发展人造地球卫星和各类空间探测器。在载人航天器方面,首先建立大型永久性载人空间站,由专用实验室、宇航员生活舱、数据处理系统等几部分组成,可供宇航员长期居住,其次是大力开发航天飞机,然后开发月球基地,并将月球作为探测其他星球的前哨基地。
近几年来,美国宇航局为了激发青少年探索字宙奥秘的兴趣和了解航天知识,利用航天飞机货舱(图7-37)中的多余空间,鼓励各国青少年提出在失重条件下各类小型的单项设计研究,进行搭机试验。这一倡议有利于发展青少年的想象力和创造力,有利于普及航天知识,得到世界各国科研和教育部门的赞赏,引起了包括我国在内的广大青少年的极大兴趣。他们提出了成千上万的设计方案,其中在失重状态下,蜘蛛是否还能结网,烛焰会是什么形状、鱼类在水中游动时是否还能保持平衡等题目,都已进行了搭机试验。

发布时间:2016/11/29 上午8:48:23 阅读次数:2329
