第7章 六、振动

机械振动

一阵微风吹过，池塘里的浮萍会上下浮动，树木的枝条也会左右摇摆。仔细观察蜜蜂、蜻蜓等昆虫在飞行时，它们的翅会很快地上下抖动。孩子们荡秋千时的来回运动，人们走路时，两只手臂会自然地、有节奏地前后摆动，这些常见的运动都有一个共同的特点，即物体（或物体的一部分）以某一位置为中心做往复运动，这种运动叫做机械振动，简称振动（vibration）。振动是自然界中和日常生活中常见的另一种周期运动。

简谐振动

有一种玩具狗（图7-38），它的头部和尾部用较软的弹簧跟身体相连。如果轻拍一下玩具狗，它便不停地摇头晃尾起来，这是弹簧引起的振动。

如果在上端固定的软弹簧下挂一个小球，将小球向下拉开一段距离后放手，小球便会上下往复运动（图7-39），这也是弹簧引起的振动。

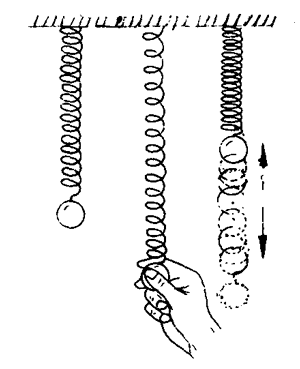
现在我们来研究上述物体产生振动的原因。为了简化问题，便于分析，可以用如图7-40的装置。把有孔的小球跟弹簧连接在一起，穿在一根光滑水平杆上，并把弹簧的左端固定，弹簧的质量比小球小得多，可以忽略，这样就组成一个弹簧振子。拉动一下小球，小球便在水平杆上振动起来。

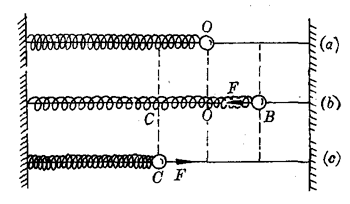
当弹簧既不拉伸也不被压缩时，小球静止在杆上的O点位置，这时小球所受合力等于零。O点就是弹簧振子的平衡位置[图7-40（a）]。

如果把小球从平衡位置O向右拉到B点，这时弹簧被拉伸。放开后，小球所受合力等于弹簧的弹力[图7-40（b）]，小球在这一指向平衡位置的弹力作用下，向左做加速运动。在振子向平衡位置O运动的过程中，弹簧的形变逐渐变小，弹力也逐渐变小，加速度也逐渐变小，但小球的速度增大。当小球经过平衡位置O时，弹簧的形变消失，弹力减小到零，加速度等于零，这时小球具有最大的速度。

由于惯性，小球不会停留在平衡位置，它将继续向左运动。但这时由于弹簧被压缩，对小球将作用一个方向指向平衡位置O的弹力，小球将做减速运动；随着小球继续向左运动，弹簧的压缩形变越来越大，作用于小球的弹力也越来越大，小球速度不断减小，当速度减小到零时，小球将到达平衡位置左侧的C点，这时，弹簧的压缩形变最大，小球受到指向平衡位置的弹力也最大[图7-40（c）]。

接着，小球将在指向平衡位置的弹力作用下，向右做加速运动。跟前面所讲的情况相类似，小球并不停止在它的平衡位置上，而要越过这个位置，再次回到B点。这就完成了一次全振动。以后小球就重复上述过程，在B、C间往复运动。

由上述分析可知，弹簧振子在振动过程中，当偏离平衡位置时，总是受到一个跟位移方向相反、能使振子返回平衡位置的力，这个力叫做回复力。弹簧振子的回复力就是弹簧的弹力。由于弹簧发生弹性形变时，弹力跟形变量成正比，对弹簧振子来说，也就是回复力F跟振子的位移x成正比，而回复力总是指向平衡位置，所以回复力的方向始终与位移的方向相厦，它们之间的关系可用下式表示：

F＝－kx，

式中比例常数k是跟振动系统有关的一个量。负号表示回复力F的方向始终跟位移x的方向相反。

物体在受到大小跟位移成正比，而方向相反的回复力作用下的振动，叫做简谐振动。

简谐振动是一种最简单、最基本的机械振动。敲击音叉后，两个股叉上的质点的振动，浮标漂浮在水面时的上、下浮动，都可以看成是做简谐振动。弹奏竖琴、钢琴、吉他（图7-41）等弹拨乐器时，琴弦的振动是比较复杂的振动，但可以看成是许多简谐振动的组合。

问题探讨

S：小球在两个相连接的、对称的光滑斜面上来回运动（图7-42），这种运动是否可看成简谐振动？

T：小球的这种运动不是简谐振动，而只是做机械振动。简谐振动是指物体受到跟位移成正比、并且总是指向平衡位置的力的作用下的振动，即F＝－kx，回复力F是一个变力。而小球在斜面上运动时受到的合力F＝mgsinθ是一个指向O点、大小不变的力，而不是跟位移成正比的力，所以不是简谐振动。

思考

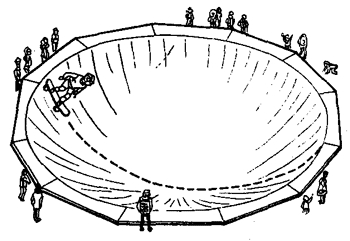
1．有一种滑板运动为青年所喜爱，滑板上装有4个轮子，踩着滑板可以在半个开口向上的圆柱形滑道或碗形滑道的内壁来回滑行（图7-43），这种滑板运动可以看作振动吗？中心位置在哪里？

2．图7-40中的弹簧振子从B点开始运动，经B→O→C→O→B，完成一次全振动。在振动过程中，如果从振子经过O点时开始计算，经O→C→O→B→O，这算不算完成一次全振动？

振动的振幅、周期和频率

用一根橡皮绳穿过一只乒乓球，将橡皮绳拉成水平后，把橡皮绳的两端固定在两个铁架台上（图7-44）。将乒乓球沿垂直于橡皮绳方向拉开一小段距离，放开后，乒乓球就以原来的平衡位置O为中心，在B、C点间振动。这时OB、OC间的距离都较小，乒乓球只发生轻微的振动。若开始时使乒乓球离开平衡位置的距离较远，则振动时OB和OC间的距离都较大，乒乓球发生比较强烈的振动。

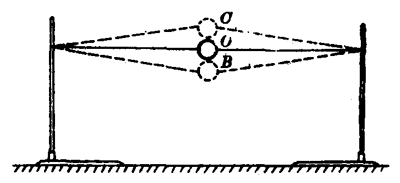
振动物体离开平衡位置的最大距离，叫做振动的振幅（amplitude）。振幅等于位移的最大值，它表示振动的强弱。图7-44中距离OB或OC就是乒乓球振动的振幅。图7-40中距离OB或OC就是弹簧振子的振幅。

若将上述实验中的两个铁架台间的距离拉大些，使橡皮绳绷得更紧，再拨动乒乓球，可以发现乒乓球的振动变快了。物理学中用周期或频率来表示振动的快慢。

振动的周期是指振动物体完成一次全振动的时间。

单位时间内完成的全振动的次数，叫做振动的频率（frequency）。频率用f表示，我国法定计量单位规定频率的单位是赫兹，符号是Hz，简称赫。每秒钟完成1次全振动的频率是1赫。

周期T和频率f有互成倒数的关系，即

T＝\(\frac{1}{f}\)，或     f＝\(\frac{1}{T}\)。

振动越快的物体，周期越短，频率越大；振动越慢的物体，周期越长，频率越小。如蜜蜂翅的振动频率为440赫，周期为2.3×10^-3秒；苍蝇翅的振动频率为200赫，周期为0.5×10^-2秒。

实验结果表明，振动物体的振动周期或频率是由振动物体本身的性质所决定的，跟振幅的大小无关，所以物体在白由状态下的振动周期或频率，分别叫做固有周期或固有频率。图7-44的实验中，如果测得这个装置振动30次的时间是12秒，它的固有周期就等于0.4秒，固有频率就等于2.5赫。固有周期和固有频率是物体的本身属性，跟物体是否振动无关。如一面锣、一根绷紧的弦、一座桥梁、一栋建筑物都具有它们各自的固有周期和固有频率。

振动图象

做简谐振动的物体，它的位移的大小和方向是随时间不断变化的。我们可以用实验方法来形象地显示这种变化。

如图7-45所示，把钢锯条的一端固定在铁架台上，另一端缚一支蘸有墨水的毛笔，拨动锯条时，毛笔的振动可看成简谐振动，调节毛笔的位置使笔尖刚能接触到放在它下面的一张纸片。如果在毛笔振动的同时，沿着垂直于笔尖振动方向匀速拉动纸片，在纸片上就描出一条曲线，从曲线可以看出笔尖的位移随时间呈周期性的变化。

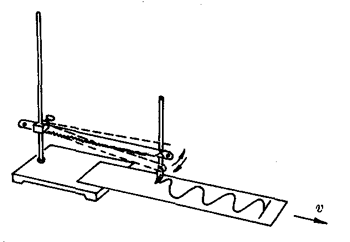
反映做简谐振动的质点的位移跟时间关系的图象，叫做振动图象。

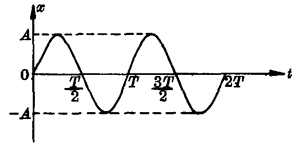
理论研究指出，简谐振动的振动图象是一条正弦（或余弦）曲线。如果取一直角坐标系，以横轴表示时间t，以纵轴表示位移x，就可描绘出一个给定的简谐振动的振动图象（图7-46）。由图象可以知道振动的周期T和振幅A的大小，还可以知道质点在任意时刻的位移。

匀速圆周运动和简谐振动的关系

匀速圆周运动和简谐振动都是周期运动，它们之间有什么关系呢？我们可以利用图7-47所示的装置进行研究。

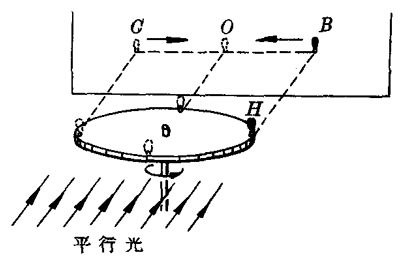
水平转台匀速转动时，转台的手柄H做匀速圆周运动。若用一束平行光，沿着转台的转动平面照射，可以看到手柄日在转台后面墙上的投影沿着一条水平线来回运动。当H运动一周，它的投影恰完成一次全振动，H做匀速圆周运动的周期和它的投影振动的周期相等，H做圆周运动的半径等于它的投影振动的振幅。可以证明，一个做匀速圆周运动的质点，它的投影是简谐振动。

内然机中活塞沿直线的往复运动，可以通过连杆、曲轴装置转变为飞轮的转动，这类转变运动形式的装置在各种机械中有着广泛的应用。但要注意，这种改变机械运动形式的装置并不反映匀速圆周运动和简谐振动的关系。

练习三十七

1．弹簧振子在振动过程中，经什么位置时速度最大？经什么位置时速度为零？经什么位置时加速度最大？经什么位置时加速度为零？

2．图7-40中的弹簧振子振动时各量的变化情况，在下面表格中已完成了一部分，试填写剩余的空格。

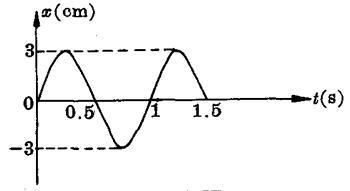
3．从图7-48所示的振动图象中，在t＝0.25秒，t＝0.5秒，t＝0.75秒时，质点的位移分别等于多大？质点完成一次全振动需时多少？

发布时间：2016/11/25 下午10:46:30  阅读次数：2449