第7章 二、匀速圆周运动

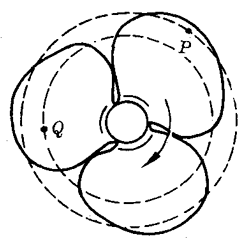
日常生活中可以见到许多转动的物体，如洗衣机的叶轮、电扇的叶片等，这些转动体上的每一个点（如图7-2所示电扇叶片上的P、Q点）的运动轨迹都是圆，这些点都在做圆周运动，它们经过一定时间，运动一周后又都回到原来位置，所以是一种周期运动。

质点沿着圆周运动，如果在相等时间里通过的圆弧长度相等，这种运动就叫做匀速圆周运动。

正常运转的洗衣机的叶轮和电扇叶片上的每一个点的运动，都是匀速圆周运动。地球沿着一个接近于圆的轨道绕太阳运动，也可以看成是匀速圆周运动。

思考

图7-3所示的是掷链球运动，在运动员拉紧链条转动身体的过程中，链球的运动能否看成是匀速圆周运动？为什么？

线速度

质点做匀速圆周运动时，它的速度方向是怎样的呢？我们可以先观察一个简单的现象。用硬纸剪成半径约2厘米的圆片，把一根火柴穿过圆心，做成一个小陀螺。在圆片的边缘滴几滴墨水，小陀螺下面衬一张白纸。转动陀螺，附着圆片边缘做圆周运动的墨水滴就飞溅开去，在白纸上留下痕迹（图7-4）。从这些痕迹可以看出，做圆周运动的墨水滴的速度方向，是沿着圆周上各点的切线方向。

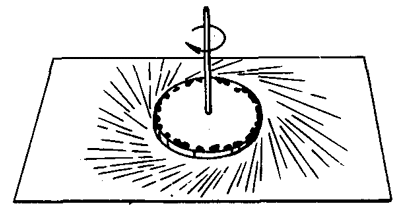
实验表明，质点做圆周运动时速度的方向在时刻改变，它在某一点（或某一时刻）的速度方向，就是圆周的这一点的切线方向。

做匀速圆周运动的质点沿圆弧运动的快慢常常是不同的。例如地球绕太阳运动时的速度大小为2.98×10⁴米/秒；使用螺旋桨发动机的飞机飞行时，桨叶尖端的速度大小接近声速（340米/秒）；而一般电钟的秒针尖端沿圆弧移动的速度大小仅为0.01米/秒左右。在匀速圆周运动中，人们用线速度来描述质点沿圆弧做匀速圆周运动的快慢程度。

线速度等于匀速圆周运动的质点经过的圆弧长度跟所用的时间的比值。

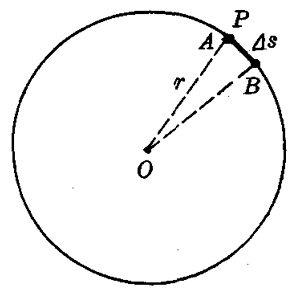
如图7-5所示，当质点P沿半径为r的圆弧，从A点运动到B点，经过弧长Δs，所用时间为Δt，那么这一质点做匀速圆周运动的线速度的大小

v＝\(\frac{{\Delta s}}{{\Delta t}}\)。

做匀速圆周运动的质点的线速度大小是不变的，但线速度的方向是时刻改变的。

线速度跟周期的关系

质点沿半径为r的圆做匀速圆周运动时，如果已知线速度为v，运动一周所用的时间（周期）为T，那么，可以得出线速度跟周期的关系

v＝\(\frac{{2\pi r}}{T}\)。

问题探讨

S：把自行车的后轮架空，转动轮子时，可以清楚地看到靠近车轮转动轴处的钢丝弯头做圆周运动，却看不清钢圈上气门芯子的圆周运动，为什么？

T：当轮子转动一周时，钢丝弯头和气门芯子也都转动了一周，即它们做圆周运动的周期T是相同的。根据关系式v＝\(\frac{{2\pi r}}{T}\)可知，当T一定时，线速度v跟半径r成正比。气门芯子做圆周运动的半径远大于钢丝弯头做圆周运动的半径，气门芯子的线速度就远大于钢丝弯头的线速度，所以你就看不清气门芯子的运动了。

角速度

质点做圆周运动的快慢也可以用角速度来描述。在图7-5中，质点P在Δt时间里从A点运动到B点经过弧长Δs时，半径OA也转过一个角度Δφ（即图中∠AOB）。我们把半径转过的角Δφ跟所用时间Δt的比值叫做圆周运动的角速度。角速度的符号是ω，写成公式就是

ω＝\(\frac{{\Delta \varphi }}{{\Delta t}}\)。

角速度的单位由角度单位和时间单位组成，在我国法定计量单位中，规定角度的单位是弧度，时间的单位是秒，角速度的单位就是弧度/秒，读作弧度每秒，符号是rad/s。

在质点做匀速圆周运动的一个周期T内，半径r转过的角度为2π，所以角速度跟周期的关系是

ω＝\(\frac{{2\pi }}{T}\)。

线速度跟角速度的关系

比较线速度v＝\(\frac{{2\pi r}}{T}\)和角速度ω＝\(\frac{{2\pi }}{T}\)两式，就可以得出线速度跟角速度的关系

v＝ωr。

思考

1．在什么条件下线速度v跟半径r成正比，在什么条件下角速度ω跟半径r成反比。你能分别举例说明吗？

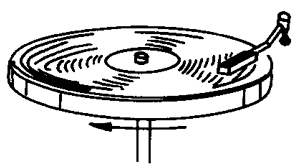
2．一般唱机的电动机转轴每分钟转数是不变的。放唱片时，拾音器（唱头）放在唱片的边缘部分（图7-6），随着唱片的转动，拾音器逐渐向唱片的中心靠近。唱片上不同半径处，在相等弧长上记录的相同频率的声振动的次数相等吗？

练习三十四

1．在半径为15米的杂技场中进行马术表演时，马沿圆形场地边缘奔跑，把马的运动看成匀速圆周运动，已知线速度是8米/秒，那么，马奔跑一周需多少时间？

2．把月球绕地球的运动看成是匀速圆周运动，已知月球与地球相距3.844×10⁵千米，月球绕地球运动一周需时27.9天，试计算月球绕地球运行的线速度大小。

3．砂轮机上的砂轮，半径是10厘米，当它以每秒18转的转速匀速转动时，砂轮边缘质点做圆周运动的角速度多大？线速度多大？离圆心5厘米处的质点的角速度多大？线速度多大？

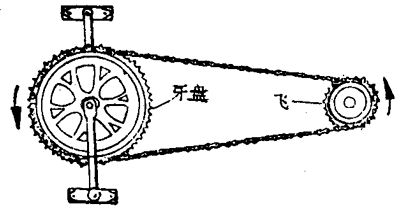
4．自行车的“牙盘”和“飞”用链条相连（图7-7），当把后轮架空，均匀摇动踏脚板时，“牙盘”和“飞”边缘的齿都可看成做匀速圆周远动。如果已知某种型号自行车的“牙盘”和“飞”的半径之比为2.4∶1，那么，“牙盘”和“飞”的周期之比是多大？角速度之比是多大？

发布时间：2016/11/22 上午8:14:34  阅读次数：826