第6章 五、机械能守恒定律

机械能

我们已经学习了动能、重力势能和弹性势能，如果我们仔细观察周围的事物，可以发现有许多物体在作机械运动时，既具有动能又具有势能。例如高空飞行的飞机，它具有一定的动能，又具有一定的重力势能。我们把动能和势能统称为机械能。

深入一步研究，我们还能发现动能和势能是可以相互转化的，例如下落的瀑布（本章导图2）就是势能转化为动能，在转化时还存在着一定的数量关系。

动能和重力势能的相互转化

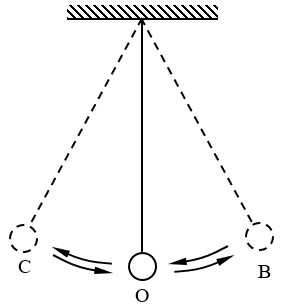
我们首先通过图6-19的实验来观察物体动能和重力势能的相互转化。如图所示，把一个钢球拴在细线的一端，把线的另一端悬挂起来，让它可以自由摆动，然后把钢球从平衡位置O拉到B，放手后可以看到钢球从B经过O摆到C，再由C经过O回到B，来回摆动。显然在B点和C点时，钢球的速度为零，动能等于零，只具有重力势能。钢球经过O点时，只具有动能，重力势能等于零（把O点所在的水平面作为h＝0的参考平面）。也就是说，钢球经过O点时的动能是由它在B点时的重力势能转化来的，钢球到达C点时的重力势能又是由它在O点时的动能转化来的。这样，由于钢球的来回摆动，它的重力势能和动能也就不停地相互转化着。

在建筑工地上，我们可以看到这样的事例：气锤在升高的过程中，克服重力做功，速度越来越小，动能不断减小，但重力势能不断增大，显然这时它的动能转化为重力势能。从高处回落的气锤情况恰好相反，在下落的过程中，重力对它作功，重力势能不断减小，但速度越来越大，动能不断增大，显然这时它的重力势能转化为动能。分析这个事例，我们不难看出动能和重力势能的相互转化，是通过重力做功来实现的。下面我们再进一步来研究这个转化过程中的数量关系。

机械能守恒定律

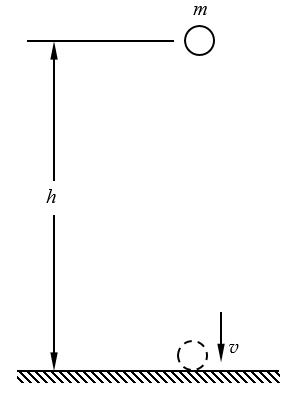
我们先以只受重力作用的自由落体为例来进行研究（图6-20）。假设物体的质量是m，它从高度是h的地方下落到地面，以地面为重力势能等于零的参考平面，则它在h高度处的重力势能E_p1＝mgh，动能E_k1＝0。当它到达地面时，重力势能E_p2＝0，动能E_k2＝\(\frac{1}{2}\)mv²。根据自由落体运动v＝gt，h＝\(\frac{1}{2}\)gt²，可得v²＝2gh，\(\frac{1}{2}\)mv²＝mgh。

可见，物体在高度为h处的机械能E₁＝E_p1＋E_k1跟物体自由下落到地面时的机械能E₂＝E_p2＋E_k2是相等的。即

E₁＝E₂。

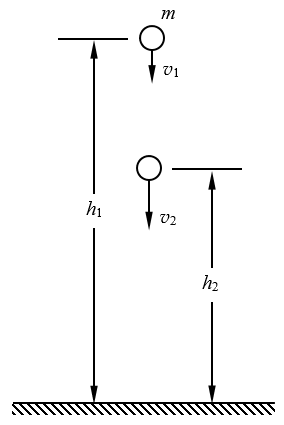
进一步研究还可以发现，前述自由落体在下落途中，从高度为h₁处下落到高度为h₂处，速度由v₁增大到v₂的过程中（图6-21），物体重力势能的变化为mg（h₁－h₂），物体动能的变化为\(\frac{1}{2}\)mv₂²－\(\frac{1}{2}\)mv₁²，根据自由落体运动

v₁²＝2g（h－h₁），

v₂²＝2g（h－h₂），

v₂²－v₁²＝2g（h₁－h₂），

可得       mg（h₂－h₁）＝\(\frac{1}{2}\)mv₂²－\(\frac{1}{2}\)mv₁²。

这就表明，物体自由下落过程中，在任意两个位置间的动能变化量和重力势能变化量总是相等的。此式经整理也可写成

mgh₁＋\(\frac{1}{2}\)mv₁²＝mgh₂＋\(\frac{1}{2}\)mv₂²，

即                         E₁＝E₂。

研究和分析都证明，在只有重力作功的情况下，物体的重力势能和动能相互转化的过程中，重力势能和动能的总和是不变的。这个结论叫做机械能守恒定律。

这个结论不仅对只受重力作用的自由落体是正确的，对任何运动物体，在只有重力做功的情况下，也总是正确的。例如物体沿光滑斜面运动就属于这种情况。

【例题1】

一辆冰橇从离地10米高处，沿弯曲起伏的滑道向下滑行。如果不计阻力，求冰橇滑到地面时的速度。

【解】冰橇在下滑过程中只受重力和滑道的弹力作用，而滑道的弹力跟冰橇的运动方向总是垂直的，它不对冰橇做功，因此只有重力对冰橇做功，冰橇的动能和重力势能的总和是守恒的。

设冰橇的质量是m，它开始下滑时的重力势能E_p1＝mgh，动能E_k1＝0。到达地面时的速度是v，重力势能E_p2＝0，动能E_k2＝\(\frac{1}{2}\)mv²。根据机械能守恒

\(\frac{1}{2}\)mv²＝mgh，

v＝\(\sqrt {2gh} \)＝\(\sqrt {2 \times 9.8 \times 10} \)米/秒＝14米/秒。

冰橇到达地面时的速度是14米/秒。

由于冰橇是沿着弯曲起伏的滑道下滑的，它经过的路径情况复杂，所受的合外力也变化不定，所以不便应用牛顿第二定律解题。而用动能和重力势能相互转化中机械能守恒的规律求解时，只要考虑运动的初始状态和终了状态，无须讨论整个过程中的细节。这样，就可以简捷地解决问题。

【例题2】

以14米/秒速度竖直向上抛出一个石子，假设不计空气阻力，那么石子上升6米距离时，它有多大的速度？石子可以上升多大距离？

【解】石子被上抛后，因不计空气阻力，只克服重力做功，它的动能转化为重力势能，而动能和重力势能的总和保持不变。

由于       v₁＝14米/秒，h₁＝0，h₂＝6米，g＝9.8米/秒²，根据

\(\frac{1}{2}\)mv₁²＋mgh₁＝\(\frac{1}{2}\)mv₂²＋mgh₂，

即得              v₂＝\(\sqrt {v_1^2 - 2g{h_2}} \)＝\(\sqrt {{{14}^2} - 2 \times 9.8 \times 6} \)米/秒＝8.9米/秒。

石子上升到6米时，它的速度为8.9米/秒。

当石子上升到最大距离h₂ʹ时，它的速度v₂ʹ为零。已知v₁＝14米/秒，h₁＝0。

根据

\(\frac{1}{2}\)mv₁²＋mgh₁＝\(\frac{1}{2}\)mv₂ʹ²＋mgh₂ʹ，

得                  h₂ʹ＝\(\frac{{v_1^2}}{{2g}}\)＝\(\frac{{{{14}^2}}}{{2 \times 9.8}}\)米＝10米。

石子能上升到10米处。

 问题探讨

S：重力势能是由物体所处位置的高度决定的。具有重力势能的物体可以是静止在高处，并不作机械运动。所以我觉得重力势能和动能不一样，把它们统称为机械能，用来量度机械运动似乎是不合理的。

T：我们把物体匀速举高要做功，但是物体的动能没有增加。放手让这个举高的物体下落，它的速度就越来越大，动能不断增大。因此我们可以理解为在举高物体的过程中，外力对物体做功，物体增加的机械能不以动能的形式出现，而以重力势能的形式被贮存了。所以在让这个物体自由下落时，由于重力做功，被贮存的机械能不断被释放出来，转化为动能的增加。所以把重力势能和动能统称为机械能来量度机械运动是很合理的。

思考

伽利略在他的理想实验中，认为在没有摩擦阻力的情况下，小球从一个斜面的一定高度处滑下，必然能在另一个相接的斜面上滑到同样的高度，不因这个斜面的倾角变化而改变。你能根据动能和重力势能相互转化中总和守恒的规律来解释吗？

功是能量转化的量度

通过前面的学习，我们知道动能和重力势能在重力做功的过程中可以相互转化。重力做多少功，动能和重力势能就转化多少，所以重力做的功就是动能和重力势能转化的量度。在这种情况下动能和势能的总和，即机械能是保持不变的，是守恒的。但是我们经常也遇到物体机械能不守恒的事例。例如，电梯匀速上升时，电梯的动能不变，重力势能越来越大，也就是机械能不断增大。电梯的机械能增大是由于电动机转动时钢索拉力对它做了功。钢索的拉力对电梯做了多少功，就有多少电能转化成机械能。

关闭发动机后的汽车，在平直路面上趟行一段距离后停止。该过程中，它的重力势能不变，动能不断减小，也就是机械能不断减小。汽车的机械能减小是由于它克服阻力做了功。汽车克服阻力做了多少功，就有多少机械能转化为内能。

可见，重力以外的力对物体做功时，物体的机械能就发生变化，机械能将跟其他形式的能发生转化。因此，不同形式的能可以通过做功相互转化，而能量转化的多少也是由做功的多少来量度的。所以，功是能量转化的量度。

功和能是不同的物理量

功是能量转化的量度，功和能有相同的量度单位，但是功和能却是两个不同的物理量。物体具有什么形式的能，具有多少这种形式的能，是由物体的运动状态决定的，所以能是描述物体运动状态的量；物体从一种能量状态转变成另一种能量状态，则必须通过做功的过程来完成，所以功是描述能量转化过程的量。状态量和过程量是不同的。由于能量既不能凭空产生，也不会无影无踪地消失，我们需要知道的只是它的转化情况。功是能量转化的量度，指出了我们可以采取以过程量来量度状态量的变化，但并非把两者等同起来。

*能量守恒定律

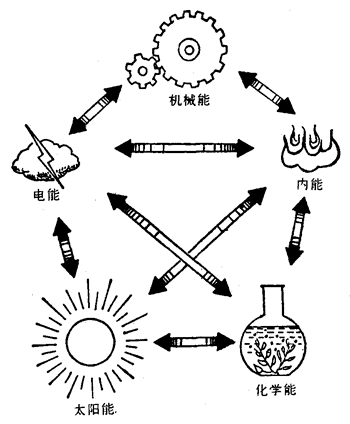
每一种形式的能都跟物质的某一种运动形式相对应，一个物体可以同时具有两种不同形式的能，例如飞行着的子弹，它既有内能，又有机械能，它的内能决定于温度和体积，而它的机械能决定于速度和高度。如果这颗子弹由于克服空气阻力做功，动能减小，温度升高，这样机械能的一部分就转化为子弹的内能。我们已经知道动能和势能是可以相互转化的，现在又知道内能和机械能也可以相互转化，而且其他形式的能都可以跟机械能或内能相互转化，总之，能的相互转化就表明了物质运动形式的转化。图6-22表示不同形式的能的相互转化。

在19世纪，许多科学家进一步关注能的转化过程中总能量是否改变的问题。德国物理学家、生理学家亥姆霍兹，在1845年发表论文，从医学角度提出了能量守恒定律。1847年，他又发表论文，在物理学领域里广泛地讨论能量守恒问题。英国物理学家焦耳，前后花了20多年时间，系统地测量了可以转化为一定热量的各种形式的能量，1850年焦耳完成了一篇总结性论文，明确指出：自然界的能量是不能消灭的，那里消耗了机械能，总能得到与它相当的热量。焦耳在实验中还发现，做一定量的电功，即消耗一定的电能来使物体温度升高时，也总是得到等量的内能。这表示在电能和内能互相转化时，总的能量也是守恒的。大量的实验事实证明，任何形式的能转化为别种形式的能时，总的能量都是守恒的。

因此，能量既不会凭空产生，也不会凭空消失，它只能从一种形式转化为别的形式，或者从一个物体转移到别的物体。这就是能量守恒定律。

能量守恒定律被称为19世纪自然科学三大发现之一，是人们认识自然和改造自然的有力武器。从物理、化学、生物到天文、地质以及各种工程技术，这一定律都发挥了重要作用，取得了重大的成就。下面我们简单介绍一个近代物理学研究中的例子——中微子的发现。在本世纪30年代初，人们发现在某些原子核反应中能量似乎并不守恒，一部分能量消失了。当时一些人就认为这些实验事实表明能量并不是普遍守恒的，但是另一些人认为在这里能量也是守恒的。奥地利物理学家泡利（1900-1958）在1933年提出，可能存在着一种当时并不知道的极其微小的粒子，所谓消失了的能量，就是被它们带走的。后来意大利物理学家费米（1901-1954）把这种粒子叫做中微子，并且发展了有关中微子的理论，认为它是一种不带电的、质量极其微小的粒子。以后人们一方面继续从理论上研究这种假设的中微子，一方面想办法用实验来探测中微子的存在。直到1956年，在人们巳经拥有核反应堆后，才在实验中证实中微子是确实存在的。这样，能量守恒定律就又一次被证实并直接导致了中微子的发现。

思考

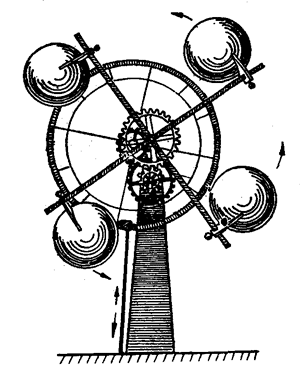
1．图6-23所示的是意大利著名画家和科学家达·芬奇（1452-1519）设计的装置。机器各臂上的金属泡里注有一部分水银，达·芬奇设想水银的移动会带动齿轮机构，使轮子转动，且带动传动装置不断对外工作。试从能量守恒定律分析，是不是有可能？

练习三十三

1．在下列事例中的运动物体，如果不计空气阻力，哪些运动物体的动能和重力势能的总和是守恒的，哪些是不守恒的？为什么？

（1）空中飞行的铅球；

（2）杯中从水面下沉的小球；

（3）被匀速拉上光滑斜面的小车；

（4）沿光滑曲面下滑的木块（图6-24）。

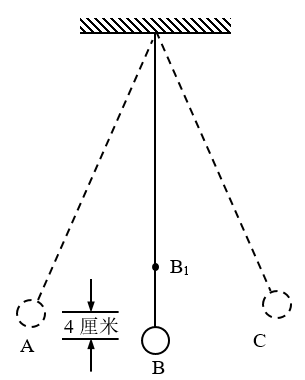
2．把用细绳悬挂着的摆球从平衡位置B拉到A（图6-25），A、B之间的高度相差4厘米。放开手，摆球就在A、C之间来回摆动。如果把一支铅笔沿垂直于摆动平面的方向放在目的位置上，摆球将上升到多大高度（不计空气阻力）？

3．蒸汽打桩机的重锤质量是250千克，它被提升10米后自由下落打击桩面。它打击桩面时具有多大的动能？速度多大？

4．滑雪运动员从20米高的山坡上滑下，如果阻力忽略不计，滑到山坡高度的一半处时，他的速度多大？

5．在地面点火引爆的爆竹，可以飞升到相当于7层楼的高度，如果测得7楼高度离地面22.5米，不计空气阻力，爆竹是以多大速度离开地面的？它上升到10米时的速度多大？

阅读材料

机械能转化和守恒定律

动能、重力势能和弹性势能统称为机械能。我们知道，在只有重力做功的情况下，物体的动能和重力势能相互转化的过程中，它们的动能和重力势能的总和保持不变。那么动能和弹性势能之间是否也能发生相互转化并且总和保持不变呢？

实验告诉我们：一个放置在光滑水平桌面上的轻质弹簧，一端固定，一端与小球相连。如果将小球从原来位置拉开一定距离，弹簧就具有一定的弹性势能[图6-26（a）]，放开小球，弹簧收缩，小球在弹簧的弹性力作用下运动起来，弹簧不断收缩，小球不断加速，表明弹性力做功使弹簧的弹性势能不断减小，小球的动能不断增大，直到弹簧恢复原状。这时弹性势能全部转化为小球的动能，小球的速度达到最大值。然后弹簧不断被压缩，小球的速度不断减小，表明弹性力做负功使弹簧的弹性势能不断增大，小球的动能不断减小，直到弹簧被压缩到跟当初拉开小球的距离相同的位置。这时小球的动能全部转化为弹簧的弹性势能[图6-26（b）]。这就是说，在只有弹性力做功的情况下，小球的动能和弹簧的弹性势能也会相互转化；在转化过程中，它们的动能和弹性势能的总和也是保持不变的，即机械能也是守恒的。

综合上述，可以得出这样的结论：

在只有重力或弹性力做功的情况下，物体系统内部的动能和势能在相互转化的过程中，机械能的总和保持不变。这个结论叫做机械能转化和守恒定律，简称机械能守恒定律，它是力学中具有普遍意义的重要定律之一。

机械的分类和机械效率

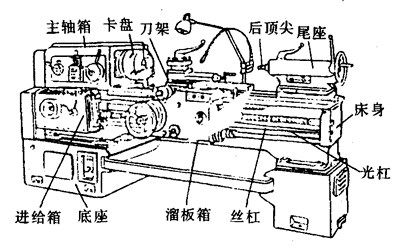
利用机械能做功或实现机械能和其他形式能相互转换的器具、装备都叫做机械，机械大致可以分为三类。第一类机械是把已有的机械能或非机械能转换成便于利用的机械能，例如风力机（本章导图1）、水轮机、汽轮机（图6-27）、内燃机、电动机等，称为动力机械。第二类机械是把机械能转化成非机械能，例如发电机等，称为能量转换机械。第三类机械是利用人力、畜力或动力机械所提供的机械能来做功，以改变施力的大小、方向或运动的快慢，满足各种工作的需要，例如车床（图6-28）、纺纱机、织布机以及各种交通工具等，称为工作机械。

工作机械做功时，动力机械提供的动力对它们做功的功率，称为工作机械的输入功率。工作机械对外界做功的功率，称为工作机械的输出功率。由于工作机械要克服机件运动时的摩擦阻力或者本身所受的重力，它们的输出功率总是小于输入功率。输出功率所占输入功率的百分比称为机械效率。显然，任何实际机械的机械效率都不可能达到100%，但是它的值的大小却是工作机械性能优劣的一种衡量标准。

本章学习要求

1．理解功的概念，知道功是能量转化的量度。

2．理解功率的概念。

3．理解动能的概念。

4．理解重力势能的概念，常识性了解弹性势能。

5．理解机械能的概念。

6．理解机械能的转化和守恒定律。

*7．知道能量守恒定律及其重要意义。

复习题

1．球员用100牛的力踢球，球滚出的距离为50米，根据W＝Fs得出球员踢球做的功是5千焦，你认为这个答案对吗？为什么？

2．一个孩子用80牛的力想把放在地面上重100牛的钢材提起来，但始终未能使钢材离开地面。在试提的过程中，孩子做了多少功？

3．在下列情况中，哪些力对物体做功？物体克服哪些力做功？哪些力不做功？

（1）关闭电动机后，在平直轨道上行驶着的地铁列车；

（2）正在匀速上坡的汽车；

（3）物体沿粗糙斜面加速下滑；

（4）空投物资匀速降落。

4．高10米的瀑布每秒钟下落50吨的水，如果全部用来冲击水轮机带动发电机发电，估计水轮机和发电机能把流水的机械能的60%转变成电能，那么发电机的输出功率有多大？

5．输出功率为4.2千瓦的车床，在切削某种钢材时的速度是7.5米/秒，问车刀克服的阻力有多大？

6．把用细绳悬挂着的摆球拉到水平位置A（图6-29），然后放手，如果细绳的长度l＝50厘米，求：

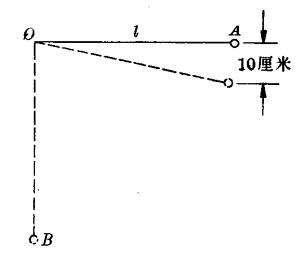
（1）摆球经过最低点B时的速度；

（2）摆球往回摆动经过比A点低10厘米高处时的速度（不计空气阻力）。

7．站在10米高的楼上，以10米/秒速度抛出一个小球，小球落到地面时的速度多大？不计空气阻力，解题时为什么不必知道小球的质量和小球抛出时速度的方向？

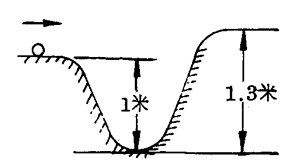
8．质量是0.4千克的小球，以2米/秒的速度滚落到一个光滑的小坑（图6-30）内，坑深1米，它的另一端高1.3米，小球能滚上另一端吗？

发布时间：2016/11/18 下午9:20:33  阅读次数：5914