第2章 六、理想气体的状态方程

前面我们已经学习了用控制变量的方法，研究一定质量的气体在体积不变时（等体积过程），它的压强跟温度的关系，压强不变时（等压过程），它的体积跟温度的关系，以及在温度不变时（等温过程），它的压强跟体积的关系，并且分别得出查理定律、盖·吕萨克定律和玻意耳定律。但在实际情况中，经常会遇到气体的温度、体积和压强这三个量中，有一个量发生变化时，会引起其他两个量同时发生变化的复杂情况。例如四冲程柴油机压缩冲程开始后，进气阀和排气阀就都关闭，这时活塞把已经吸入气缸的一定质量的空气压缩，气缸内空气体积迅速减小的同时，它的温度和压强都急剧地增大，到压缩冲程末，当气缸内空气体积减小为原来体积的\(\frac{1}{{20}}\)时，温度可升高到700℃，压强可高达4×10⁶帕，这时向气缸内喷入雾状燃油，燃油立即燃烧。再如图2-27（a）所示的竖直放置的U形管中，封闭端内有一定质量的气体，当气体温度升高时，它的体积膨胀了，压强也一定相应增大[图2-27（b）]。

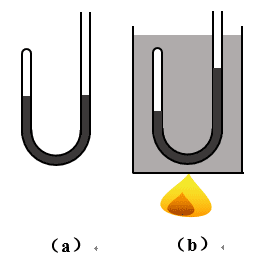
怎样研究一定质量气体的温度、体积和压强三个量同时发生变化的情况呢？它们在发生变化的过程中，是否也具有某种规律呢？

理想气体

气体的三个实验定律是研究上述情况的基础，但它们都是在温度不太低、压强不太大（相对于室温和通常的大气压强）的情况下得出的。如果在温度很低、压强很大的情况下，实验结果将会出现很大偏离，而且在温度非常低、压强非常大时，真实气体可能已经变成液态甚至变成固态了。为了便于研究问题，我们可以设想一种气体模型，这种气体在任何温度和压强下，都将严格遵循上述研究气体热学性质的实验定律，这种气体叫做理想气体。

物理模型

物理学是研究物质运动最一般的规律和物质的基本结构的科学。在实际情况中，影响物质运动变化的因素往往是复杂的。为了简化问题，有利于所研究的问题的逐步展开和顺利解决，在物理学研究中常常忽略一些次要因素，而只考虑起决定作用的主要因素，因此，就需要建立物理模型。

例如把物质分子看成一个个不连续的弹性小球，在物质三态中有着不同的空间分布与结构，这就是物质结构的分子模型。

为便于研究真实气体的性质，建立了理想气体模型，并假设它有如下性质：

1．分子之间除碰撞外，不存在分子作用力。

2．分子只有质量而无体积，理想气体可以无限压缩。

这些假设使在研究真实气体时能抓住气体的主要性质与特征，忽略在低温、高压下跟气体实验定律之间出现的偏离，从而使研究的问题得以简化。

建立物理模型是一种科学方法，在今后学习中经常用到。

理想气体状态方程

如图2-28（a）所示，在一个带有活塞的竖直放置的容器里，盛有一定质量的理想气体，它的温度为T₁，体积为V₁，压强为p₁，这是它的一个平衡状态，设为状态1。

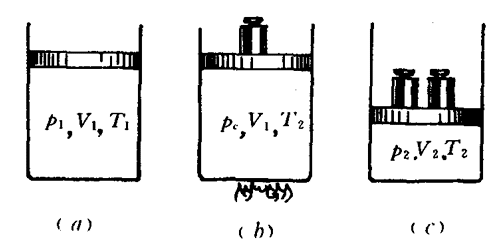
如果要使它变化到另一个平衡状态2，这时的温度为T₂（T₂＞T₁），体积为V₂（V₂＜V_l），压强为p₂（p₂＞p₁）[图2-28（c）]。设想这一定质量的气体是先后经过两个过程来实现这一状态变化的。假定它先经过一个等体积过程，到达某一个中间状态C，这时的温度T_C＝T₂，体积保持不变V_C＝V₁，压强为p_C。[图2-28（b）]。根据查理定律，可得出在这过程中压强跟温度的关系是

\(\frac{{{p_1}}}{{{p_C}}}\)＝\(\frac{{{T_1}}}{{{T_2}}}\)                             （1）

然后使气体再经过一个等温过程到达状态2，这时温度仍为T₂，体积为V₂，压强为p₂[图2-28（c）]。根据玻意耳定律，可得出这过程中压强跟体积的关系是

p₁V₁＝p₂V₂。                      （2）

从（1）式得p_C＝\(\frac{{{p_1}{T_2}}}{{{T_1}}}\)，代入（2）式，整理后得

\(\frac{{{p_1}{V_1}}}{{{T_1}}}\)＝\(\frac{{{p_2}{V_2}}}{{{T_2}}}\)。

这个方程叫做理想气体状态方程。表明一定质量的理想气体的压强和体积的乘积，除以它的热力学温度得到的商，在状态变化过程中是保持不变的。即

\(\frac{{pV}}{T}\)＝C（常数），

式中C跟气体的质量和性质有关。理想气体状态方程反映了一定质量理想气体的温度、体积和压强这三个状态量间的关系，对于真实气体来说，在温度不太低、压强不太大的情况下也是适用的。

理想气体的状态方程实际上包含了前几节所学过的气体实验定律。例如温度不变时（T₁＝T₂），理想气体状态方程就是玻意耳定律的表达形式；体积不变时（V₁＝V₂），理想气体状态方程就是查理定律的表达形式；压强不变时（p₁＝p₂），理想气体状态方程就是盖·吕萨克定律的表达形式。

在应用理想气体状态方程解决实际问题时，要注意气体的质量必须是一定的，气体先后所处的两个状态的压强和体积应分别取相同的单位，而温度则必须用热力学温度表示。

【例题】

如图2-29所示，两个容积相等的容器A和B，用一细管相连，关闭阀门S，将容器B抽成真空。容器A中有一定质量的气体，压强为1.0×10⁵帕，温度为27℃。打开阀门S，一部分气体将从容器A进入容器B。如果两个容器中的气体温度都降低到10℃，这时容器A内的气体压强是多大？

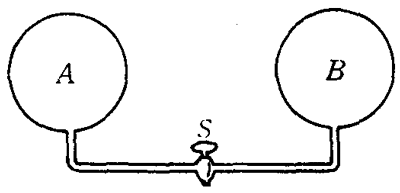
【解】容器A中一定质量气体初始状态的体积设为V₁，温度T₁＝（273＋27）开，压强p₁＝1.0×10⁵帕。阀门S打开后，气体体积增大为V₂＝2V₁，温度降低为T₂＝（273＋10）开。达到平衡后，容器A内的气体压强与容器B中的气体压强是相等的，设为p₂。

根据理想气体状态方程

\(\frac{{{p_1}{V_1}}}{{{T_1}}}\)＝\(\frac{{{p_2}{V_2}}}{{{T_2}}}\) 

得           p₂＝\(\frac{{{p_1}{V_1}{T_2}}}{{{V_2}{T_1}}}\)＝\(\frac{{1.0 \times {{10}^5} \times {V_1} \times (273 + 10)}}{{2{V_1} \times (273 + 27)}}\)帕＝\(\frac{{283}}{{600}}\)帕＝0.47×10⁵帕。

即容器A内的气体压强为0.47×10⁵帕。

可见，容器中气体压强比原来减小一半还多。这是因为气体体积增大到原来2倍的同时，气体的温度也降低的缘故。

问题探讨

S：一定质量的理想气体在状态变化时，是否可能温度升高体积反而减小？如果可能的话，跟盖·吕萨克定律是否相矛盾？

T：一定质量的理想气体在状态变化时，温度升高，只要压强同时增大，体积减小是有可能的。如内燃机在压缩冲程中，气缸内气体的情况就是这样。这跟盖·吕萨克定律并不矛盾，因为盖·吕萨克定律是在气体压强不变的条件下（即等压过程中）才适用，而你假定的状态变化是p、V、T三个量都在发生变化的。

练习七

1．一个沼气泡从池塘底升起到达水面。若已知池水深5米，池底温度为17℃，水面温度为27℃，大气压强为1.0×10⁵帕。这一沼气泡自池底升到水面时体积增大为原来的几倍？

2．某一内燃机吸入气缸的燃料混和气的压强为1.0×10⁵帕，温度为47℃。在压缩冲程末，气缸内混和气的压强达到1.2×10⁶帕，压缩前、后混和气的体积之比是6∶1，压缩后气缸内混和气的温度升高到多少摄氏度？

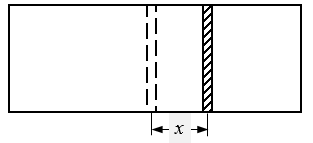
3．如图2-30所示，气缸总容积为20升，内有一个面积为0.04米²的绝热活塞，把气缸分隔成两部分。开始时，活塞左、右两侧空气的温度、压强、体积都相等，活塞在气缸的正中央恰保持平衡。现使气缸内活塞左侧空气温度升高到47℃，活塞右侧空气温度降低到0℃，试求活塞最终平衡时的位置。

4．某一定质量的理想气体在状态1时的温度为T₁，体积为V₁，压强为p₁。如果先让它经过一个等温压缩过程，到达某一中间状态C，使压强增大为p₂，体积减小为V_C；再经过一个等压膨胀过程，到达状态2，使它的温度升高为T₂，体积增大为V₂。试利用有关的气体实验定律推导出理想气体的状态方程。

发布时间：2016/11/10 上午10:23:54  阅读次数：2119