第十三章A 万有引力定律

导学

• 在本章中，你将学习：
• 什么是万有引力定律？它是如何被发现的？
• 科学家们是怎样发现宇宙结构的？
• 恒星是由什么物质组成的？
• 恒星是如何演化的？

浩瀚宇宙，星移斗转，天体不停地运动和演化。天文观测到的结果表明，宇宙中存在着约由3 000多亿颗恒星组成的银河系和1 000多亿个河外星系。飞向宇宙，一直是人类的梦想。1977年8月20日，“旅行者”2号空间探测器（图13-1）发射升空。12年后的1989年8月24日，它在探访了海王星后飞出太阳系，一直飞向宇宙深处。在这个探测器上放有一张可以保存10亿年的镀金唱片，它录制了代表人类文明的各种声音，包括一首中国古曲《高山流水》。人们期待着这个探测器能有一天被地外文明的某个智慧生命族类发现，并从这张名为《地球之声》的唱片上知道我们的存在。这张唱片的开始有这样一段话：

“这是一个来自遥远的小小星球的礼物。它是我们的声音、科学、形象、音乐、思想和感情的缩影。我们正在努力使我们的时代存留下来，使你们能了解我们生活的情况。我们期待着有一天解决我们面临的问题，以便加入到银河系的文明大家庭中来。这个‘地球之声’是为了在这个辽阔而令人敬畏的宇宙中寄予我们的希望、我们的决心和我们对遥远世界的良好祝愿。”

大家谈

1．如果“旅行者”2号这个太空“漂流瓶”会在某一天被地外的智慧生命发现，它们能理解我们的音乐、思想和感情吗？

2．如果你有机会向太空中的其他智慧生命族群说明你已掌握的最重要的物理知识，你会如何表达？

开普勒利用丹麦天文学家第谷遗留的大量天文观测资料发现，火星运动的轨迹不是圆，而是椭圆，并且运行速度不均匀。1609年，开普勒发表了著名的第一和第二定律。开普勒第一定律把太阳的位置精确标定在椭圆的一个焦点上，各行星都在椭圆轨道上绕太阳运行。开普勒第二定律也叫“面积定律”，提出了行星与太阳的连线在相等时间内扫过的面积相等，这在本质上阐明了行星离太阳近则快、远则慢的不匀速性[图13-2（c）]。1619年，开普勒又在《宇宙和谐论》一书中发表了开普勒第三定律，即行星绕太阳一周所需时间的平方跟椭圆轨道半长径的立方之比是一个常量。开普勒的发现为人类对天体运动规律的认识作出了巨大的贡献。牛顿正是在开普勒等人的发现基础上，开始探寻引力的奥秘。

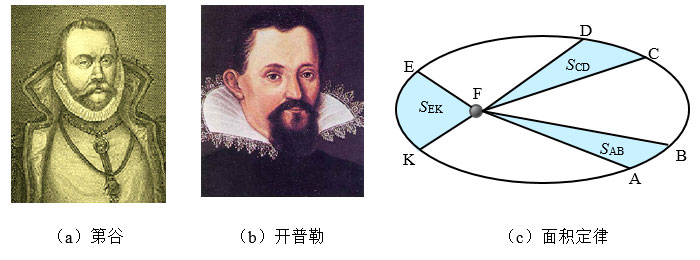
大家谈

如前所学，任何物体做圆周运动都必须有向心力。太空中没有长长的钢链，究竟是什么神秘的力量能使遥远的星球不断改变运动方向、绕着太阳运动呢？

使天体不断改变运动方向的是什么力？

科学巨匠牛顿在哥白尼、第谷、开普勒、笛卡儿、伽利略等人奠定的基础上，完成了一系列重大的科学研究。根据牛顿在晚年的回忆，当他对着天空看月亮时，恰好一个苹果从树上掉下，这时灵感来到他脑海中：作用在苹果上使苹果落地的力与作用在月亮上使月亮做圆周运动的力可能是同一个源，即地球的引力。当时，只有牛顿才能把这两个司空见惯、似乎毫不相干的事件联系了起来。经过严密论证，证明这种力的大小与距离的平方成反比。他又认为，这种地球引力与太阳对行星的作用力及一个行星对其卫星的作用力是相同的。牛顿把这种所有物体之间都存在的相互吸引力叫做万有引力。

1．万有引力

任何具有质量的物体间都存在相互吸引的作用力，这种相互吸引的作用力就叫做万有引力。

万有引力的大小如何确定？

牛顿发现了万有引力，并在前人的基础上，总结出万有引力定律：自然界中任何两个物体间都相互吸引，引力的大小与物体的质量的乘积成正比，与它们之间距离的平方成反比。这里所指的距离是指可以看成质点的两物体间距离，若是两均匀球体则是球心间距离。若用m₁、m₂分别表示两物体质量，r表示两物体间距离，则万有引力

F＝G$\frac{m_1{m}_2}{r^2}$。

式中G叫做引力常量。由精确实验测量可知，G＝6.67×10^-11N·m²/kg²。G的数值等于两个质量为1kg的物体相距1 m时，它们之间万有引力的大小。

2．万有引力定律（law of universal gravitation）

两个物体间的引力大小，跟两物体质量的乘积成正比，跟两物体距离的平方成反比，方向在两物体连线上，这就是万有引力定律。万有引力定律可用下面的公式来表示

F＝G$\frac{m_1{m}_2}{r^2}$。

引力常量是如何测量得到的？

限于当时的条件，还不能在实验室直接验证万有引力定律。直到100多年后，英国科学家卡文迪什才利用扭秤这一巧妙的实验装置[图13-3（a）]解决了测量G值的问题。

扭秤的主要结构[图13-3（b）]就是在石英丝上装一个平面镜，利用平面镜对光线的反射，显示石英丝极微小的扭转角，从而测量出极微小的万有引力，验证了万有引力定律，并测出引力常量G的值。

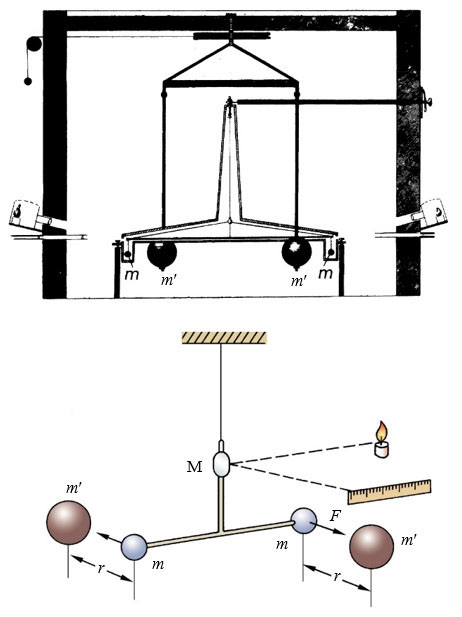
3．卡文迪什实验

卡文迪什利用扭秤实验验证了万有引力定律，并测出了引力常量。

大家谈

1．既然地球吸引苹果和吸引同球的力都是万有引么苹果会掉到地上，而月球不会掉下来？

2．如果有一天万有引力突然消失，世界将发生什么变化？

【示例】地球表面的物体所受到的重力也遵循万有引力定律，已知地球的质量m＝5.976×10²⁴ kg，地球半径r＝6.371×10⁶ m。求地球表面重力加速度的大小。

分析：在地球表面，物体所受重力的大小可看作地球对它的万有引力的大小，知道了引力常量和地球质量m，就可计算重力加速度的大小。

解答：设物体质量为mʹ，由mʹg＝G$\frac{m{m}^{\prime }}{r^2}$可得

g＝G$\frac{m}{r^2}$＝6.67×10¹¹×$\frac{5.976\times {10}^{24}}{{(6.371\times {10}^6)}^2}$≈9.82 m/s²。

发布时间：2016/9/14 上午11:37:19  阅读次数：1285