第六章 B 气体的压强与体积的关系

你参加过充气用品展示会吗？图6-13所描述的就是这类展示会的一角。现代社会生活中充气用品的应用非常广泛，如充气门、充气棚、充气安全滑梯、充气救生垫、充气皮划艇，乃至充气沙发等，它们都是在一个橡胶袋或塑料容器内充入气体制成的，其中有的全密封，有的可不断补充气体。这些容器内的压强通常都大于外界气压，当它们受到冲击而变形，体积发生变化时，其内部气体的压强也会变化。关于气体压强与体积变化的关系正是本节所要研究的内容。

大家谈

气态是物质存在的一种状态，你认为应该如何来描述局限在某一容器中的气体状态呢？

可以用哪些物理量来描述气体的状态？

我们来看一个演示实验。在上端有活塞的厚玻璃筒底部放置一块硝化棉，如图6-14所示。用手快速向下压活塞，请你观察所发生的现象。

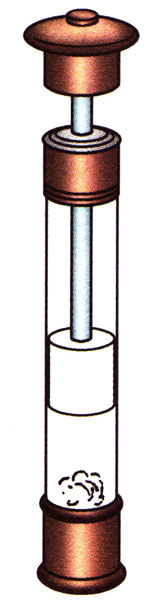
在这个实验中，我们发现，当用手快速向下压活塞时，密封在玻璃筒里的气体的体积、温度、压强都发生了变化，我们就说气体的状态发生了变化。体积、温度、压强等都是用来描述气体状态的物理量，我们称之为气体的状态参最。只要其中任何一个状态参量发生变化，我们就说该气体的状态发生了变化。

1．气体的状态参量

在物理学中，要用体积、温度、压强等物理量来描述气体的状态，这几个物理量被称为气体的状态参量。

怎样确定气体的体积和温度？

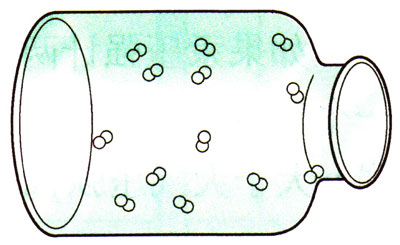
由于气体没有一定的形状，具有流动性。不论容器多大，气体分子总能充满整个容器，如图6-15所示。因此任何容器的容积就是该容器内气体的体积。

我们已知道，气体的温度是描述气体冷热程度的物理量。从微观角度分析，气体温度的高低取决于气体分子无规则运动的剧烈程度。气体分子运动越剧烈，分子运动的平均速率越大，气体的温度就越高。

我们经常用温度计来测量气体的温度。在下一节，还会用DIS系统结合温度传感器来测量温度。

气体的压强是怎样产生的？

让我们先做一个实验来模拟压强的产生。把磅秤的托盘翻过来放置，将若干小钢珠（或黄豆）连续倒在托盘上（图6-16），小钢珠与托盘撞击后全部都被反弹开去，但由于许多小钢珠不断地撞击托盘，托盘就受到一个持续的压力，磅秤上就会指示这一压力。当然，气体分子不像小钢珠那样，由于受重力作用而只沿着一个方向运动，但气体压强的产生确实是由于组成气体的大量分子向各个方向运动，并撞击器壁而产生的。气体压强的大小与每个分子的质量、运动速度大小和单位时间内在单位面积上碰撞的分子数等有关系。

（1）气体体积

气体分子所能达到的空间范围称为气体的体积，用字母V来表示。体积的国际单位是m³（读作立方米）。

（2）温度。

温度（热力学温标）用字母T表示，国际单位是K（读作开尔文，简称开）。日常生活中，温度常常采用摄氏温标，用字母t表示，单位℃（读作摄氏度）。

（3）气体的压强。

容器壁单位面积上所受的压力就是气体的压强。用字母p表示，国际单位是Pa（读作帕斯卡，简称帕）。

下面我们介绍一些测量气体压强的方法。

（1）用汞压强计测量

测量时，将汞压强计竖直放置，并将装有待测气体的容器与它的U形管的一臂连通。如果汞压强计两臂内汞面的高度相等，如图6-17（a）所示，表明容器中气体的压强p等于大气压强p₀，即

p＝p₀。

如果汞压强计两臂内汞面的高度差为h，且与容器连通的一个臂内汞面较低，如图6-17（b）所示，表明容器内气体的压强p大于大气压强p₀，且有

p＝p₀＋ρgh，

式中ρ为汞的密度。

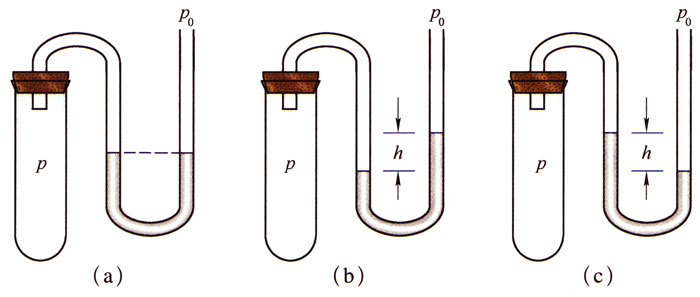
如果汞压强计两臂内汞面的高度差为h，但与容器连通的一个臂内汞面较高，如图6-17（c）所示，表明容器内气体的压强p小于大气压强p₀，且有

p＝p₀－ρgh。

（2）用指针式或数字式压强计测量

盛放在储气筒里的压缩空气和盛放在钢瓶里的氧气或氢气的压强，通常是用指针式金属压强计或数字式压强计直接显示的。图6-18显示的是用指针式压强计来测量自行车内胎气压的情景。

自主活动

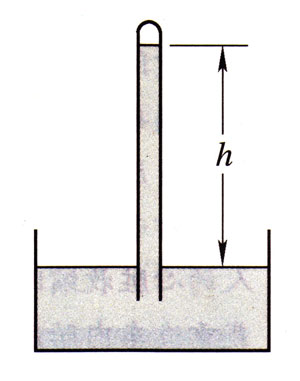
图6-19所示是托里拆利测量大气压强的实验装置示意图，把一端封闭的、充满汞的玻璃管倒置并竖直插入汞槽内，如果有部分空气漏入管内，管内外汞面高度差为h，设大气压强是p₀，则管内汞柱上方的气体压强为多少？

示例

一个气缸水平放置在地面上，在质量为m₁、截面积为S的活塞上方放置一个质量为m₂的重物，平衡时如图6-20所示，则气缸内气体的压强为多少？（大气压强为p₀）

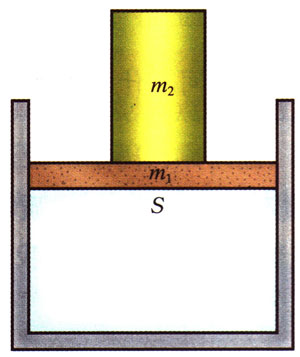
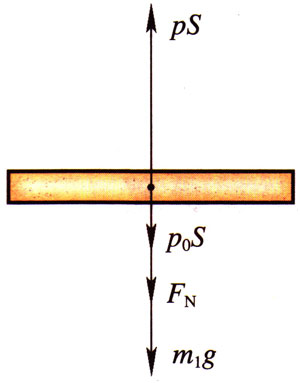
【分析】由于活塞处于静止状态，一定受到平衡力的作用。此时活塞受到自身重力m₁g、重物向下的压力F_N＝m₂g和大气向下的压力p₀S，如图6-21所示。这三个力正好与气缸内作用于活塞、方向向上的气体压力pS相平衡。

【解答】根据物体平衡的条件，有

pS＝m₁g＋m₂g＋p₀S，

所以，p＝p₀＋\(\frac{{{m_1}g + {m_2}g}}{S}\)。

【讨论】在研究气体压强大小的时候，往往要考察与气体直接接触的物体，如活塞、汞柱等，通过分析这些物体的受力情况，可得出气体的压强。

点击

有关压强的一些数据p/Pa

气体的压强与体积之间有什么关系？

图6-14所示的演示实验表明，一定质量的气体，其体积、压强和温度之间存在着一定关系。下面我们先来研究控制气体温度不变时气体压强与体积的关系。气体在温度不变的条件下发生的状态变化过程叫做等温过程。

人们很早就知道一定质量气体的体积变大压强就会减小的事实，但压强与体积之间的定量关系直到300多年前才被发现。1661年6月18日，英国化学家、物理学家玻意耳（Robert Boyle 1627—1691）公布了他的实验结果——“空气是可以压缩的”，并且指出这种可压缩的空气体积与加在气体上的压强成简单的反比关系。这就是人们所熟知的玻意耳定律。下面我们通过实验探究来得出这个规律。

2．在温度不变的条件下，一定质量的气体压强与体积的关系

学生实验

用DIS研究温度不变时，一定质量的气体压强与体积的关系

【实验目的】

探究一定质量的气体在温度不变条件下的压强与体积间关系。

【实验器材】

DIS（压强传感器、数据采集器、计算机等）、注射器。

【实验结论】

________________________________________________________________________。

探索研究（DIS实验）

将压强传感器接入数据采集器。开启电源，运行DIS应用软件，点击实验条目中的“研究温度不变时，一定质量气体的压强与体积的关系”，软件界面见图6-22。

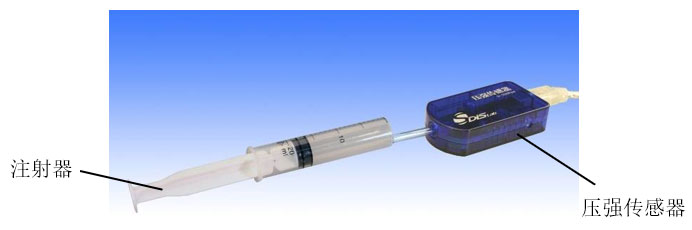
如图6-23所示，注射器与压强传感器的测口相连。在数据表格上输入所设定的体积；推拉注射器活塞，使其位于各设定体积时，点击“记录数据”，表格上将记录不同体积时所对应的注射器内气体的压强数据。点击“数据计算”，表格上将显示注射器内气体压强和体积的乘积值，以及体积的倒数值。计算出pV乘积，并和其他组同学进行比较。

【反思讨论】

为什么各组同学实验的pV值不完全相同？在实验中，推拉活塞需要注意什么？

启动“图线分析”功能，在屏上可分别观察到压强和体积、压强和体积的倒数的关系曲线。请在下表中抄录计算机界面上测得的压强和体积的数据。

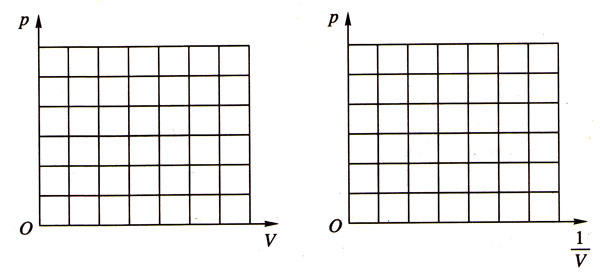
根据抄录的数据，参考屏幕上得出的图线，在图6-24中用描点法画出p与V以及p与的关系图，并分析得出结论。

（1）玻意耳定律（Boyle law）

一定质量的气体在温度不变时，它的压强与体积成反比

\(\frac{{{p_1}}}{{{p_2}}}\)＝\(\frac{{{V_2}}}{{{V_1}}}\)

或写成

p₁V₁＝p₂V₂

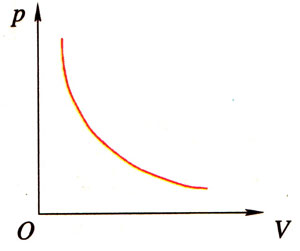
（2）等温线（isotherm）

在平面直角坐标系中，纵轴表示压强p、横轴表示体积V。p与V的函数图像是一条双曲线，如图6-25所示。这种表示等温过程的p-V图像叫做等温线。

点击

体积变化导致压强变化的微观机制

从分子动理论的角度分析可得，当一定量气体的体积减小时，单位时间内撞击单位面积的分子数增加，从而导致单位面积上受到的作用力增大，这样气体的压强就会变大。

自主活动

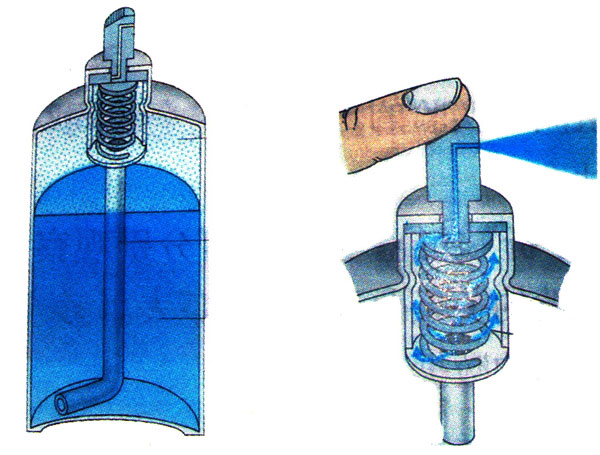
玻意耳定律在日常生活中有许多实际应用。图6-26中所示是家用杀虫剂罐的内部构造和使用示意图，请分析其工作原理。

示例

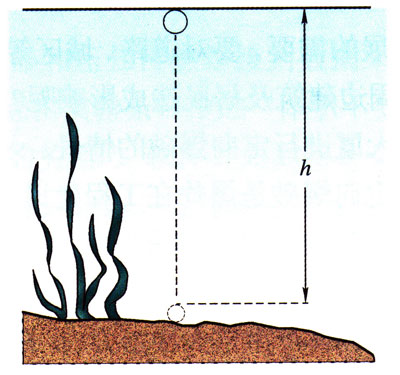
一个体积为V的沼气泡自池塘底浮起，如图6-27所示。若水深为3m，沼气泡从池底上升到水面时，它的体积将变为原来的多少倍？（设水底和水面温度相同，大气压强p₀＝1.0×10⁵Pa，水的密度ρ＝1.0×10³kg/m³）

【分析】由于水底和水面温度相同，而且气泡在上升过程中质量没有发生变化，应该遵循玻意耳定律，只要算出气泡在水底和水面的内部气体压强，即可求出体积的变化情况。

【解答】在池底时，气泡内部气体压强p₁＝p₀＋ρgh，体积V₁＝V；当气泡浮到水面后，气体压强p₂＝p₀，体积为V₂。根据玻意耳定律

p₁V₁＝p₂V₂。

所以，

V₂＝\(\frac{{{p_1}{V_1}}}{{{p_2}}}\)＝\(\frac{{({p_0} + \rho gh)V}}{{{p_0}}}\)＝\(\frac{{(1.0 \times {{10}^5} + 1.0 \times {{10}^3} \times 9.8 \times 3)}}{{1.0 \times {{10}^5}}}\)V≈1.29V。

【讨论】在应用玻意耳定律解题时，首先要搞清楚是否满足温度不变和气体质量不变的条件，然后分清两个不同状态的压强和体积值，在运算过程中不一定要统一用国际单位，只要方程两边使用的单位相同就可以了。

发布时间：2016/5/27 下午1:49:33  阅读次数：4561