第五章 F 机械能守恒定律

游乐场中有一个惊险、刺激的游艺项目，那就是高架滑车，示意图见图5-39，它还有一个名称叫做“发疯的老鼠”。在图5-40所示的实物中，一辆载有数人的小车，从高处慢悠悠地起动，而后在没有任何动力情况下自行下滑。开始时速度很小，随着轨道转弯、下降，小车速度越来越大，使人感到似乎随时有冲出轨道的危险。当小车到达最低位置时速度达到最大，然后沿轨道逐渐回升。本章导学中的能量穿梭机也有这样的特点。

一辆滑车在下滑过程中既然没有什么动力，为什么能够达到令人紧张的高速度呢？

自主活动

提桶会不会碰鼻？

如图5-41所示，在一个提桶内放一些重物，用绳子将它悬挂在门框下。你自己站在门的里边，将提桶拉离竖直方向，使它凑近自己的鼻子，然后轻轻放手，提桶将向前摆去，接着又反向摆回来。当摆动很快的提桶再一次接近你的鼻子时，你敢不敢镇定自若地站在那里不动？

在这个例子中涉及势能和动能之间的转换，这种转换是有规律的。如果不知道这个规律，就会产生害怕的感觉。

我们已经知道一个物体可以具有动能，也可以具有势能，还可以同时具有动能和势能。在做功的过程中物体的动能和势能可以相互转化，例如光滑小球从斜面下滑，高度越来越低，重力势能越来越小，重力势能到哪里去了？仔细观察后你会发现，虽然小球的高度越来越低，但它的速度越来越大。原来，重力势能不断转化为动能，所以重力势能渐渐减少，而动能渐渐增大。小球竖直上抛，则是相反的例子，它的动能渐渐转化为重力势能。

不仅重力势能和动能之间可以发生转化，弹性势能和动能之间也可以发生相互转化，例如弓的弹性势能可以转化为箭的动能。

因为决定动能和势能大小的都是质量、速度、位置等力学量，我们把动能和势能统称为机械能。因为动能和势能都是标量，因此一个物体的机械能就等于它的动能和势能的代数和。动能和势能的相互转化就是机械能范围内不同形式能的转化。

1．动能和势能的相互转化

在做功的过程中，动能、重力势能和弹性势能之间可以相互转化。

2．机械能（mechanical energy）

动能、势能统称为机械能。

动能和重力势能的转化过程中存在怎样的数量关系呢？下面让我们用DIS来探究这种关系。

DIS实验

【实验1】

观察由同一位置释放的摆锤，当摆线长度不同时，摆锤上升的最大高度。

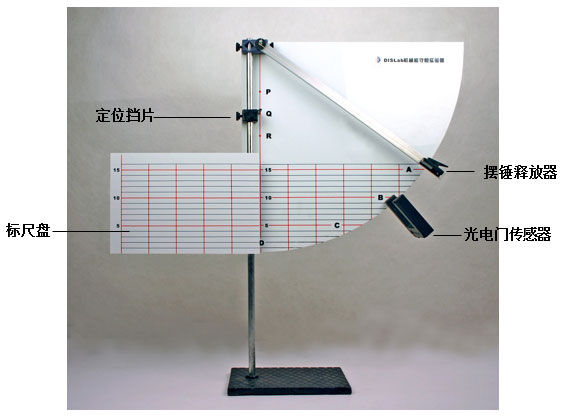
如图5-42所示，实验时先卸下“定位挡片”，将摆锤（圆柱形）置于A点，释放摆锤，观察它摆到左边最高点时的位置，用笔记下这个位置，看看这个高度与A点位置是否相同？

装上定位挡片并置于P点位置，它对摆绳有阻挡作用。再次释放摆锤，同样观察摆锤向左摆起的最大高度，记下这个位置。

依次将定位挡片下移至Q、R等位置，重复上述实验。做类似观察、记录。

从实验结果可得出什么结论？

【实验2】

将实验装置中的光电门传感器接入数据采集器。测定摆锤在某一位置的瞬时速度，从而求得摆锤在该位置的动能，同时输入摆锤的高度，求得摆锤在该位置的重力势能，进而研究重力势能与动能转化时的规律。实验中A、B、C、D四点相对于摆锤最低点的高度为0.150m、0.100m、0.050m、0.000m，已由计算机默认，不必输入。若选用其他点，则需测量实际高度并输入数据。

开启电源，运行DIS应用软件，点击实验条目中的“研究机械能守恒定律”，软件界面如图5-43所示：

测量摆锤的直径Δs及其质量m，将数据输入软件界面内。把光电门传感器放在标尺盘最底端的D点，并以此作为零势能点。

将摆锤置于A点，点击“开始记录”，同时释放援锤，摆锤通过D点的速度将自动记录在表格的对应处。

点击“数据计算”，计算D点的重力势能、动能和机械能。依次将光电门传感器放在标尺盘的C、B点，重复实验，得到相应的数据。

比较上述实验结果中各位置的机械能，在实验误差允许范围内，看看有什么特点？从中可得出什么结论？

学生实验

用DIS研究机械能守恒定律

【实验目的】

研究动能和重力势能转化中所遵循的规律。

【实验原理】

分别测定摆锤在摆动过程中任意时刻的动能和势能，研究机械能的总量有什么特点。

【实验器材】

机械能守恒实验器、DIS（光电门传感器、数据采集器、计算机等）。

【实验结论】

实验1的结论：______________________________________________；

实验2的结论：_______________________________________________。

由以上DIS实验可得出机械能守恒的结论，也可运用牛顿定律和运动学公式通过理论推导得出机械能守恒定律，这一项任务同学们在以下“自主活动”中就能独立完成。

自主活动

如图5-44所示，倾角为θ的光滑斜面上的A处有一质量为m的木块，A处离地面高为h₁。木块自静止起沿斜面匀加速滑下，在滑行过程中经过某任意位置B时的速度为v，位置B离地面高度为h₂。

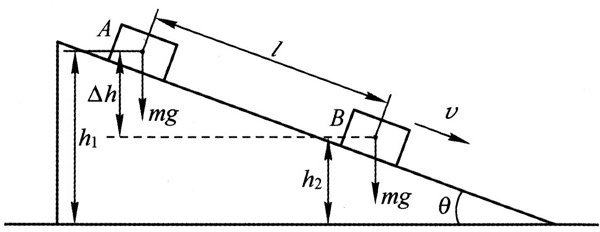
（1）写出木块在位置A的总机械能E_A＝_____________。

（2）写出木块在位置B的总机械能E_B＝_____________。

（3）运用牛顿第二定律和初速为零的匀加速运动公式证明

E_A＝E_B。

现在我们可以得出结论：在只有重力做功的情况下，物体机械能的总量保持不变，或者说机械能是守恒的。这是力学中的一条重要规律。

3．机械能守恒定律（law of conservation of mechanical energy）

在只有重力做功的情况下，物体的动能和重力势能发生相互转化，但机械能的总量保持不变，这个规律叫做机械能守恒定律。

若质量为m的物体在初位置的高度为h₁、速度为v₁，在末位置的高度为h₂、速度为v₂，那么机械能守恒定律的表达式为

mgh₁＋$\frac{1}{2}$mv₁²＝mgh₁＋$\frac{1}{2}$mv₁²

或

E_p1＋E_k1＝E_p1＋E_k1

即

E₁＝E₂

点击

有其他力做功时的机械能

在动能和势能的转化中，如果除了重力外还有弹力做功，而其他外力都不做功，机械能仍然守恒，机械能守恒定律应当表述为：在只有重力和弹力做功的情况下，物体的机械能总量保持不变。

如果除了重力和弹力做功，还有其他外力（如摩擦力）做功，则物体的机械能总量将发生变化，机械能不再守恒，机械能守恒定律在此条件下不再成立。

示例

图5-45是一条高架滑车的轨道示意图，各处的高度已标在图上。一节车厢以1m/s的速度从A点出发，最终抵达G点，运动过程中所受阻力可以忽略。试问：

（1）车厢在何处重力势能最大？在何处动能最大？在哪一段路程中动能几乎不变？

（2）车厢的最大速度是多少？

（3）如果车厢的质量为1×10³ kg，当它抵达G点后要在水平轨道上通过外界制动装置使它停下。车厢克服制动装置的阻力要做多少功？（g取10 m／s²）

【分析】通常以地面为零势能面。车厢在运动过程中轨道的支持力总是垂直于轨道，不会做功，阻力不计，只有重力做功，因此机械能是守恒的。这时重力势能的减少量一定等于动能的增加量。由于重力势能与高度有关，于是就可以根据车厢离地面的高度来确定它在该处重力势能和动能的大小。高度越低动能就越大，高度不变则动能不变。

在运用机械能守恒定律进行计算时，必须先确定研究对象，并判断运动过程是否满足机械能守恒定律的条件；然后列出初始位置及末位置的动能和势能的表达形式；再写出机械能守恒定律的方程，通过求解方程、代入数据得出结果。

【解答】（1）图5-45中A是轨道的最高点，因此车厢在A处重力势能最大；D是轨道的最低点，因此车厢在D处重力势能最小，动能最大；在C附近，轨道的高度几乎不变，重力势能几乎不变，因此车厢在这里的动能几乎不变。

（2）设A处为初始位置，其高度为h₁，此处车厢速度为v₁。根据上面的分析，D处动能最大，因此速度也最大，所以设D处为末位置，其高度为h₂，此处车厢速度为v₂，根据机械能守恒定律应有

mgh₁＋$\frac{1}{2}$mv₁²＝mgh₁＋$\frac{1}{2}$mv₁²

消去m，可得

v₂＝$\sqrt{2g(h_1-h_2)+v_1^2}$＝$\sqrt{2\times 10\times (40-5)+1^2}$m/s＝701 m/s＝26.5m/s。

因此，车厢的最大速度为26.5m/s。

（3）设A处为初始位置，G处为又一个末位置，其高度为h₃。A处机械能和G处机械能也相等。由于功是能量变化的量度，可知，高架滑车在G处附近克服阻力所做的功，应等于滑车在G处制动前后机械能的减少量。

滑车在A处的机械能与滑车在G处制动前的机械能相等，即

E_A＝E_G前＝$\frac{1}{2}$mgh₁＋mv₁²；

而滑车在G处制动后的机械能只有重力势能，没有动能，

E_G后＝mgh₃；

滑车在G处制动前后机械能之差就是所求克服阻力所做的功，

W＝E_G前－E_G后＝mgh₁＋$\frac{1}{2}$mv₁²－mgh₃＝m[g（h₁－h₃）＋$\frac{1}{2}$v₁²]＝10³×[10×（40－10）＋$\frac{1}{2}$×1²]J≈3×10⁵J。

怎样理解机械能的增加和减少？

由以上例题可以知道，在只有重力和弹力做功的条件下，机械能守恒，如果除了重力和弹力外，还有其他外力做功，则机械能不守恒。如果机械能不守恒，那么减少的机械能到哪里去了？增加的机械能又从何而来？

通过前面的学习，我们知道除重力和弹力外的其他力对物体做功，物体的机械能增加。物体克服除了重力和弹力之外的其他力做功，机械能减少。由于功只是能量转化的一种量度，所谓其他力对物体做功，实际上就是将其他形式的能转化为机械能，所谓克服其他力做功，就是将机械能转化为其他形式的能。

因此，当机械能变化的时候，增加的机械能是由其他形式的能转化而来，减少的机械能转化为其他形式的能。总之，如果不符合机械能守恒条件，机械能与其他形式的能就发生转化，其他形式的能是什么？以后我们再深入讨论这个问题。

4．机械能和其他形式能的转化

如果除了重力和弹力外，还有其他外力对物体做功或物体克服其他外力做功，机械能的总量将发生变化，这是机械能不再守恒，机械能和其他形式的能将发生转化。

英语角

Power Measment

It is often necessary to determine the power input and/or the power output of a machine, e.g.,a motor or engine.One method to do this is by the use of a dynamometer.A dynamometer is a device that measures force.

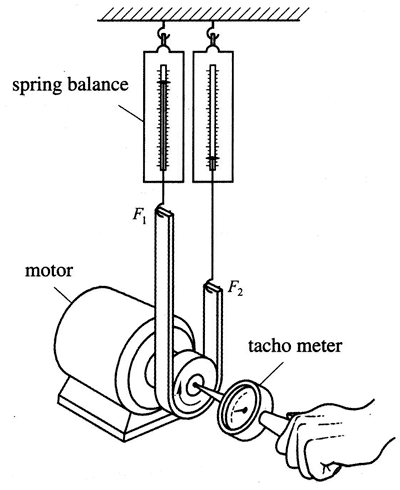
In one common type of dynamometer,the force is measured by braking action.One of the first such dynamometers was developed by the Frenchman Gaspard de Prony （1755-1839） and is called a Prony brake.The principle of the Prony brake is illustrated in Fig.5-46.

The shaft of the test motor is coupled directly to a revolving drum with tension friction belt.As the motor turns,the frictional force on the belt is measured.

In Fig.5-46,the measurement is made by the spring balances, and f＝F₂ - F₁.In one rotation, the force acts through a distance equal to the circumference（2πr）of the drum,and the work per revolution is

W＝fd＝（F₂ – F₁）（2πr）

Where r is the radius of the drum.The power is then given by multiplying the work by the rotational frequency n of the motor,which is usually given in revolution/sec(rps),ie.,

P＝（F₂ – F₁）（2πr）n

发布时间：2016/5/20 下午9:00:48  阅读次数：2130