第五章 A 功

自然界的一切物质都具有能量，但是对于不同的运动形式，能量的形式也不一样，各种形式的能量还可以相互转化。

在本篇中你将重点了解机械运动和热运动中的能量及它们之间的转化，并懂得能量转化中遵循的规律。

导学

在本章中你将了解：

• 什么是功和功率？
• 什么是动能和势能？
• 功和能有什么关系？
• 动能和势能相互转化时遵循什么规律？

你一定还记得本教材的前言中曾提到的能量穿梭机，如图5-1所示。如果你曾参观过科技馆，那么对它的印象一定相当深。

在这个展品中，动力装置将一个个小球逐一提升到高处，然后让它们滚下。小球沿着导轨做各种形式的运动，有直线运动、圆周运动、螺旋运动、抛体运动，时而上、时而下、时而慢、时而快，小球遵循的运动规律中就有能量变化的规律。学习了本章之后你将能分析和解释这些有趣的现象。

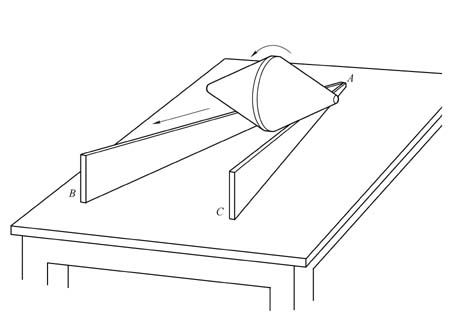
如图5-2所示，两块三角形的木板B、C竖直放在桌面上，它们的顶点连结在A处，底边向两边分开。一个锥体置于A处，放手之后，奇特的现象发生了，锥体自动地沿木板滚上了B、C板的高处。锥体真的能自动由低处向高处滚动吗？

在初中我们已经学过功的概念。大家都知道，人们发明的许多机械都是用来做功的。图5-3所示是明代科学家宋应星的《天工开物》中记载的我国早期的提水机械桔槔。在战国时期《庄子》卷五《天运篇》中说：“……大桔槔者手引之则俯，舍之则仰。”图5-4所示是现代大型起重机，它能吊起近百吨的货物。运用这些机械的过程中涉及重力、弹力和摩擦力等，我们把这些力所做的功叫做机械功（mechanical work），简称功。

<

机械做功还有一个重要的特点，任何机械可以省力或者省距离但不能省功，这个结论叫做功的原理。

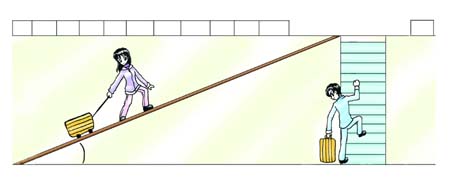
如图5-5所示，旅客要将笨重的带滑轮的行李箱从地面搬移到平台C上。若沿着竖直的扶梯A提上去很费力，若沿着斜坡B匀速拖上去则十分省力。但两者做的功是相同的，这是为什么呢？学习本节之后你将能解释这个问题。

怎样才能做功？

大家谈

在图5-6中分别画出了举重运动员的三种运动情况，图（a）表示上举过程，图（b）表示挺住不动，图（c）表示匀速向前移动。请你说说在这三种情况下运动员都做功吗？你认为怎样才能做功？

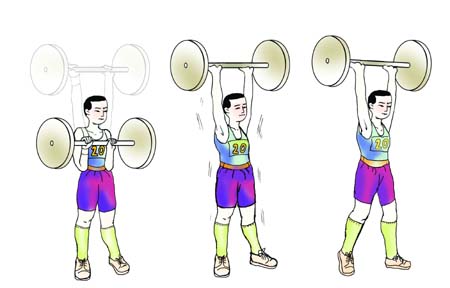
由以上讨论可知，只有物体在力的方向上产生位移，我们才能说这个力做了功。可见，物理学中“功”的概念与工作的“工”以及立功受奖的“功”是有区别的。

1．功（work）的要素

如果有力作用在物体上，而且物体在力的方向上发生位移，我们就说力对物体做了功。

力和物体在力的方向上的位移，是做功的两个不可缺少的要素.

怎样计算功的大小？

在初中阶段我们已经知道功的计算式是

W＝Fs。

式中，F表示物体受到的力，s是物体在力的方向上通过的距离，现在我们叫做位移。在国际单位制中，功的单位是焦，用符号J表示。但是这个计算式只适用于力和位移方向一致的情况，在一般情况下，力的方向和位移方向并不在一条直线上，这时可以用矢量分解的方法来处理。

如图5-7所示，拉力F的方向与物体位移s的方向成θ角。这时我们可以将F分解为与位移方向一致的分力F₁和与位移方向垂直的分力F₂。根据功的定义可知，只有F₁是做功的。而F₁＝Fcosθ，于是可以得到W＝F₁s＝Fscosθ。F₂的方向跟位移s的方向垂直，物体在F₂的方向上没有位移。所以，力F₂所做功等于零。

这样，我们可以得到一般情况下功的计算式：

W＝Fscosθ。

2．功的计算

力对物体所做的功W等于力的大小F、位移的大小s、力和位移之间夹角θ的余弦三者的乘积。

功的计算式为

W＝Fscosθ

自主活动

某同学用16N的力沿拖把柄方向斜向下推动拖把，如图5-8所示，拖把柄与地面夹角始终是30°，拖把前进了0.5m，则推力做的功是多大？

由公式W＝Fscosθ可知，功的大小不仅决定于力和位移，还决定于力和位移之间的夹角θ。下面我们讨论当θ不同时，做功的几种情况。

当θ＝$\frac{\pi }{2}$时，cosθ＝0，W＝0，这时力的方向与位移的方向垂直，力不做功。

当0≤θ＜$\frac{\pi }{2}$时，cosθ＞0，W＞0，这时力做的功为正值。

当$\frac{\pi }{2}$＜θ≤π时，cosθ＜0，W＜0，这时力做的功为负值。

可见功是标量，可以是正值，也可以是负值，还可以等于零。

3．正功和负功

当W＞0时，力对物体做正功，或者说力对物体做功。

当W＜0时，力对物体做负功，或者说物体克服力做功。

在上面的“自主活动”中，我们用公式计算了一个力做功的大小，而实际上物体可能受多个力。如果要求物体所受合力所做的功，可以有两种方法。第一种方法是先把合力F求出来，然后用公式W＝Fscosθ计算合力所做的功；第二种方法是先把每个分力所做的功算出来，然后求它们的代数和，也就是说，合力所做的总功等于每个分力所做功的代数和。这两种方法的计算结果是一样的。

示例

如图5-9所示，有一重为200N的载货车被光滑运输轨道限制，只能沿轨道运动。轨道的水平部分高h＝3m，倾斜部分由B处直达C。一工人在轨道的水平部分以恒力F从A点向右推载货车，F＝10N，其方向与水平面的夹角θ为30°。从A处推至B处后撤去推力，AB距离为4m。到达B处后载货车沿轨道BC滑下。试分别计算载货车从A处至C处的过程中，推力F所做的功和重力G所做的功以及总功。

【分析】载货车从A到B的过程中，推力与位移的夹角小于90°，推力做正功；而重力与位移的夹角等于90°，重力不做功。载货车沿轨道BC滑下的过程中，推力已经撤消，不再做功；而重力与位移的夹角小于90°，重力做正功。

【解答】货物运动情况如图5-10所示。

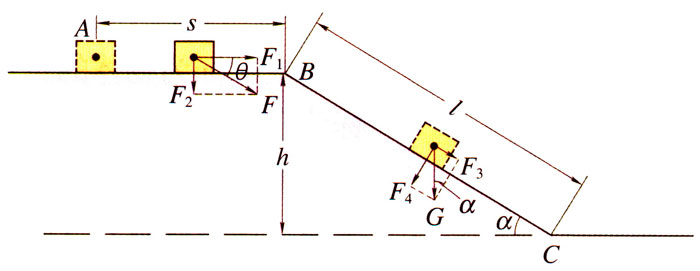
货物在平台上运动时，推为F可分解为沿位移s方向的分力F₁和垂直于位移s方向的分力F₂，F₁＝Fcosθ，F₂＝Fsinθ。

根据功的计算公式，推力F所做的功

W_F＝Fscosθ＝10×4×$\frac{\sqrt{3}}{2}$J＝34.6 J。

货物在斜面上运动时，重力G可分解为沿斜面方向的分力F₃和垂直于斜面方向的分力F₄。设斜面长为l，斜面与地面夹角为α，则F₃＝Gsinα，F₄＝Gcosα。

这时重力所做的功

W_G＝F₃l＝Glsinα。

由于lsinα＝h，所以重力所做的功

W_G＝Gh＝200×3J＝600J。

合力所做的总功等于每个分力所做功的代数和

W_总＝W_F＋W_G＝34.6J＋600J＝634.6J。

【讨论】由以上解题过程可知，在计算某个力做功时，只要将这个力乘以物体在这个力的方向上的位移就可以了，与其他力是否存在、是否做功无关。本题中求货物下滑时重力所做的功，实际上可以直接用W_G＝Gh来计算。也就是说，重力做多少功，只要考虑和计算竖直方向上的位移，它的大小就是物体移动前后的高度差。而总功则等于每个分力做功的代数和。

自主活动

讨论这样一个问题：一个排球被击出后竖直向上运动，到达最高点又回落下来，考虑空气阻力，在它上升和下降过程中分别受到什么力的作用？这些为做的是正功还是负功？

怎样用图像表示功的大小？

功的大小也可以用图像来描述，图5-11表示恒力做功的情况，图中横坐标为物体的位移s，纵坐标为在位移方向上的作用力F，画出的图像（水平线）反映力与位移的关系，该图叫做F-s图。想一想，图线下的阴影面积表示什么？

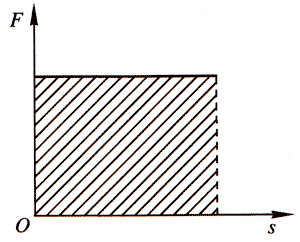
4．功的图示

在F-s图中，表示F与s关系的曲线和坐标轴所包围的面积表示功的大小。

拓展联想

变力做的功

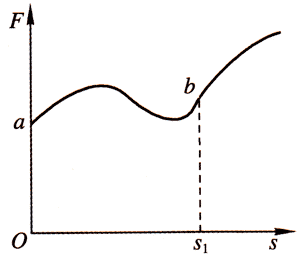
如果在做功的过程中，力发生变化，我们叫做变力做功，变力做功时的F-s图如图5-12所示。

图形abs₁O的面积就表示变力F在位移s₁段做功的大小。

我们已经知道，在弹性限度内弹簧的弹力与形变成正比，即F＝kx，试在图5-13中画出弹簧的弹力随位移变化的图像，并思考怎样利用该图像计算弹簧在伸长了x₁的过程中弹力做的功。

发布时间：2016/4/7 下午3:14:15  阅读次数：3328