第四章 C 机械振动

本节我们将学习另一种周期运动——振动。振动也是常见的运动形式，甚至可以说我们生活在振动的世界中。汽车、火车、飞机在运行时都发生振动；蚊子翅膀每秒数百次的振动，会发出我们听得见的声音，各种乐器正是由于振动才能产生美妙的音乐；对于人体来说，心脏跳动、肺的呼吸、脑电波的涨落等也都是振动；地震则是一种强烈的、有很大破坏性的振动。

图4-22所示的秋千和图4-23所示的钟摆，摆动时都在做振动。我们可以通过荡秋千活动来观察和体验振动过程中人体的位移和速度的周期性变化，你还能举出其他的振动实例吗？

振动最主要的特征是什么？

人们通常从最简单、最基本的情况入手研究物理问题。在图4-24中，有一根水平的光滑金属杆，杆上穿有质量为m的带孔小球，一根轻质螺旋弹簧一端固定，另一端和小球相连接，这样就构成了一个弹簧振子。我们可以通过考察弹簧振子的振动过程来探究振动的特征，了解引起振动的原因，发现振动的规律。

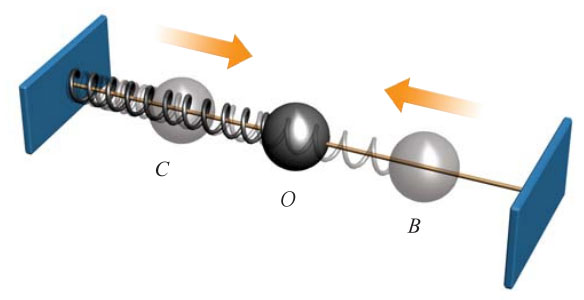
大家谈

在仔细观察弹簧振子的振动后，请你归纳出弹簧振子振动的主要特征是什么？

很明显，弹簧振子是在一个中心位置（图中O点）附近做周期性往复运动，凡具有这个特征的机械运动叫做机械振动。进一步观察可以发现，无论弹簧被压缩或被拉伸，弹簧对小球的作用力都是指向中心位置O，这个力叫做回复力，正是这个回复力才使得小球发生振动。中心位置有时又叫做平衡位置，在该位置小球不受回复力的作用。

如果弹簧振子从某位置出发再次回到该位置，并保持与出发时相同的运动方向，我们就说弹簧振子完成了一次全振动。

1．机械振动（mechanical vibration）

物体在某一中心位置附近所做的往复运动叫做机械振动，简称为振动。

产生机械振动的条件是存在指向平衡位置的回复力

2．全振动（vibration in one period）

做振动的质点从某位置出发第一次回到该位置，并保持与出发时相同运动方向的过程叫做一次全振动。

下面我们来研究弹簧振子在一次全振动的过程中的位移、回复力（所受弹力）、加速度和速度的变化情况。

图4-25表示弹簧振子在9个不同时刻的位置，相邻时刻的时间间隔都相等，它反映了一次全振动过程中振子的位移随时间的变化规律。图中画出了坐标系，竖直向下的坐标轴表示时间，水平向右的坐标轴表示小球球心离开平衡位置的位移。

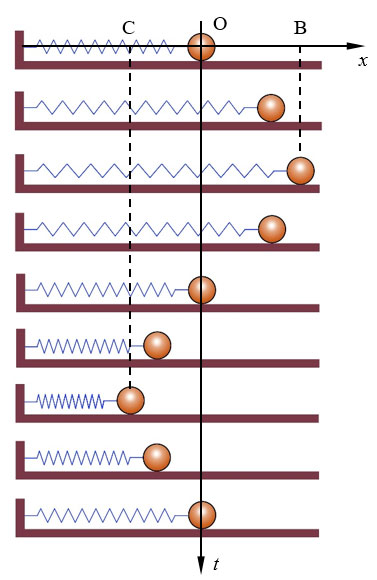
自主活动

现在请完成以下任务：

（1）用力的图示定性表示各时刻小球所受弹簧的弹力。

（2）用光滑曲线在图上连接各时刻小球球心的位置。

（3）把小球的位移、回复力（所受弹簧的弹力）、加速度和速度的变化情况填在下表空格中（选填“增大”或“减小”）。

完成这些研究后我们可以体会到，在振动过程中，物体的位移、回复力、加速度和速度都在不断发生周期性变化。

振动过程比较复杂，如何描述它呢？

为了研究振动，需要用一些物理量来描述不同振动的特征。

振动物体总是在一定范围内做往复运动的，图4-25中小球就是在B和C的两点之间运动，小球在振动过程中，不同的时刻离开平衡位置的距离是不同的，小球离开平衡位置的最大距离叫做振幅。

不同振动物体完成一次全振动所需要的时间往往各不相同，我们把完成一次全振动所需要的时间叫做振动的周期，振动的周期与物体振动的快慢有关。周期越短，振动越快。同样，不同振动物体在单位时间内完成全振动的次数也往往各不相同，我们把振动物体在单位时间内完成全振动的次数叫做频率，频率也与物体振动的快慢有关，频率越高，振动越快。

3．振动的描述

（1）振幅（amplitude）。

物体在振动过程中，离开平衡位置的最大距离叫做振幅，振幅通常用符号A表示。振幅的单位是m。

（2）周期（period）。

物体完成一次全振动所需要的时间叫做周期，用符号T表示。周期的单位是s。

（3）频率（frequency）

单位时间内完成全振动的次数叫做频率，用符号f表示。频率的单位是Hz（读作赫兹）。

振动的频率f与周期T的关系式

f＝$\frac{1}{T}$

示例1

在图4-25中，振子小球的位移、所受回复力、加速度和速度在什么位置最大？在什么位置最小？为什么？

分析：这是一道分析说理题，要求先明确题中涉及的物理过程，然后根据相关物理知识，进行推理分析，并作出科学简洁的表述。

小球的位移是以中心位置O为起点的，离O点越远，位移越大。小球所受回复力就是弹簧的弹力，弹簧形变越大，即位移越大，回复力也越大。小球质量不变，由牛顿定律，竖直方向合力为零，水平方向的回复力与加速度成正比，回复力最大的位置，加速度也最大。速度大小则与加速或减速运动的过程有关。

解答：小球在B或C位置，位移大小等于振幅，达到最大，而在O点位移为零，应是最小。小球在B或C位置，弹簧的形变最大，回复力达到最大，加速度也最大；而在O点，弹簧的形变为零，回复力等于零，加速度也为零。小球在从O点到B或C位置的过程中，一直在做减速运动，到达B或C位置时，不能继续向前，速度减为零，而小球在从B或C位置到O点的过程中，一直在做加速运动，到达O点后，马上要做减速运动，所以在O点小球的速度为最大。

示例2

图4-26是一张频闪摄影照片，显示了一个弹簧振子在半个周期中7个时刻的位置，频闪时间间隔为0.1 s，照片与实际长庋之比为1∶4。则：

（1）求该弹簧振子的振幅、周期和频率。

（2）根据这张照片对弹簧振子振动过程中的速度变化情况进行分析。

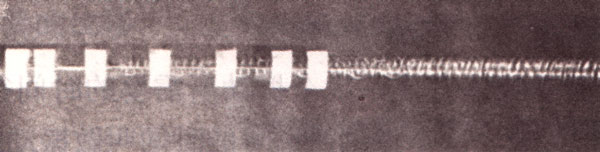
分析：由振子不同时刻位移的对称性可知，图中自右向左第四个振子中心的位置是这个弹簧振子的平衡位置。从照片可以看出位移并不严格对称，这是实际情况与理想情况的差别所造成的。由平衡位置至最右或最左振子中心位置的距离，或者由最右与最左振子中心的距离可算出振幅；从半个周期中频闪摄影次数和频闪时间间隔可以得到周期；再利用频率与周期的关系式可算出频率。此外，由于频闪时间间隔恒定，照片上两相邻振子之间的距离也就近似反映了该处附近振子的速度的大小。

解答：（1）利用直尺量出照片中最右端与最左端振子中心的距离约是3.9cm，再考虑到照片与实际线度之比可知，振子振动的振幅是A＝7.8cm。

半个周期内，频闪摄影所经历的时间为0.1s×6＝0.6s。所以振子振动的周期T＝1.2s，频率f＝$\frac{1}{T}$＝$\frac{1}{1.2}$Hz＝0.83Hz。

（2）恒定时间间隔内振子的位移大小反映了它的平均运动速度。因此从照片上可以看出，振子在平衡位置（图中自右向左第四个振子中心的位置）附近的速度最大，在离开平衡位置位移最大处，速度最小。

STS

常见振动的频率

人耳对声音频率的感觉范围是20～20000 Hz。低于这个频率的声音称为次声；高于这个频率的声音称为超声。男低音歌唱家发出的声音频率可低到约60Hz，女高音歌唱家的声音频率可高达1200Hz。

构成物质的分子、原子也都在振动，固体分子、原子的振动频率很高，通常达到10¹⁴Hz。

地球、太阳的“呼吸”和“歌唱”

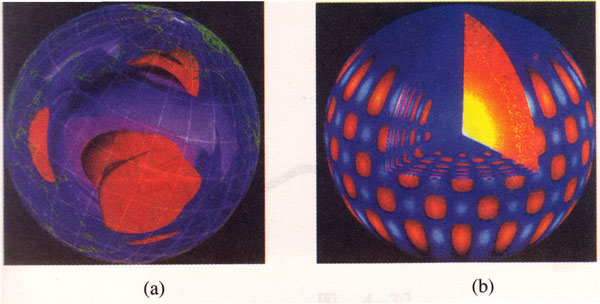
在图4-27中，图（a）表示地球内部流淌着液态岩浆层，它使地球表面有规律地在10^-4mm线度内上升或下降，结果产生了地球的“呼吸声”。现在，地震学家利用仪器已经探测到地球的这种振动。图（b）表示太阳内部的旋涡状气体使之有规律地膨胀或收缩。从这张计算机模拟图上可以看到，太阳表面蓝色的地方表示太阳在向外扩展，红色的地方表示太阳在向内收缩，这样一张一缩就产生了振动。假如宇宙中有空气，我们在地球上或许还能“听”到太阳在“歌唱”。

振动对生理的影响

有资料表明，动物低频率的叫声能让骨折的骨头更快愈合。音乐可以影响人的脑电波和呼吸的节奏，从而改变人的意识状态。以德国古典作曲家巴赫、维瓦尔第等人的作品为代表的巴洛克音乐具有放松情绪的作用，甚至能使心跳频率降到与音乐节奏大致相同的每分60次。音乐还有助于植物生长、奶牛产奶、减轻病痛和帮助记忆等。

拓展联想

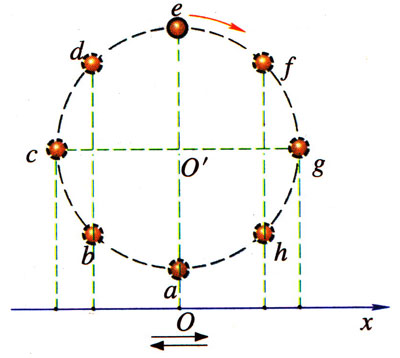
匀速圆周运动和振动都是周期运动，它们之间有什么联系？请看图4-28，小球沿半径为r的圆周按顺时针方向做匀速圆周运动，小球在水平直线上的投影就在该直线上做振动。小球历经a→b→…→h→a各点运动一周，它在水平直线上的投影恰好完成一次全振动。小球做匀速圆周运动的周期与它的投影振动的周期相等；小球圆周运动的半径等于它的投影振动的振幅。

发布时间：2016/3/24 下午2:38:56  阅读次数：2026