第四章 A 匀速圆周运动

导学

在本章中你将知道：

• 什么是周期运动？
• 什么是圆周运动、机械振动、机械波？
• 如何描述各种周期运动？
• 各种周期运动在生产和生活中有哪些应用？

我们身边有许多运动是不断重复进行的，如小孩在地面上拍皮球时皮球的运动，游乐场里的秋千、摩天轮和荡船的运动，自然界中的日落日出、彗星回归、海浪起伏等，还有生产中木工锯木时锯子的往复动作、自动装配线上机械手的动作、各类机器工作时运动部件的重复运动……这些现象有的比较简单，有的比较复杂，但它们都表现出一个共同的特点，就是运动不断重复。如果运动物体从任一时刻开始，每经过一定的时间，它的位移、速度、加速度等完全恢复到与该时刻的相同，这种运动就叫做周期运动，每重复一次运动所需的时间叫做周期。

图4-1所示是游乐场的荡船的运动，图4-2所示是实验室水槽中的人造波浪的运动，图4-3是哈雷彗星轨道示意图，哈雷彗星每隔76年就要在地球附近出现一次。这些都是周期运动的实例。

自主活动

测量自己呼吸和脉搏的周期。要求先不用任何仪器，凭感觉猜测自己呼吸一次、心跳一次所用的时间，记在纸上。再考虑选择适当的仪器和方法，测出自己呼吸和脉搏的周期，与自己的猜测比较。还可以与同学相互测量，验证各人的测量结果。

如果物体沿着一个圆周运动，我们就说物体在做圆周运动。很多常见的圆周运动都是周期运动，在生活中做圆周运动的物体很多，例如娱乐场所的空中转椅在运行时就做圆周运动。高度在100m以上的空中转椅又叫做摩天轮。图4-4是位于上海市锦江乐园的摩天轮，它的高度为108m，直径98m，每次可乘坐378人，坐在轿厢内的游客转一圈需25min。当你坐在开动着的摩天轮上，从高空饱览美丽风光的同时，你就正沿着一个圆周在运动。

除了摩天轮外，在生产、生活和自然界中还有很多物体在做圆周运动，如图4-5所示的家用洗衣机转筒上的各点、图4-6所示的旋转餐厅的座椅、图4-7所示的旋转木马上的游客等。

圆周运动和直线运动有什么不同？

以前我们学习的运动都是直线运动，也就是说质点的运动轨迹是一条直线，本节要讨论质点沿着圆周的运动。圆周运动和直线运动有两点不同：第一，当然是它们运动的轨迹不同；第二，这两种运动产生的条件不同。

1．圆周运动（circular motion）

质点沿着圆周所做的运动，就是圆周运动。

质点做直线运动的条件是质点不受力，或者所受合外力等于零，或者所受合外力的方向与质点速度的方向在同一直线上。如果质点不受力，或者所受合外力等于零，它将做匀速直线运动；如果所受合外力的方向与速度方向相同，它将做加速直线运动；如果所受合外力的方向与速度方向相反，它将做减速直线运动。那么质点做圆周运动的条件是什么呢？为了研究这个问题，我们先做一个小实验，然后展开讨论。

自主活动

用一根细绳拴住一个小球或一串钥匙，如图4-8所示，抡动细绳使小球或钥匙做圆周运动，感受手对绳的拉力，并说明为什么？

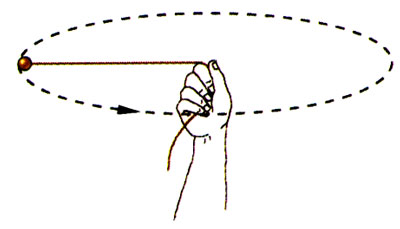
根据自主活动中的体会，我们从理论上分析质点做圆周运动的条件。

由牛顿定律可知，外力不仅可以改变速度的大小，还可以改变速度的方向。质点在做圆周运动时，它的速度方向不断改变，这是外力作用的结果。在自主活动的小实验中，这个外力就是细绳对小球或钥匙的拉力。

也就是说，如果质点做圆周运动，那么质点所受的合外力或者合外力的某个分力一定指向一个固定的圆心。这个不断改变质点运动方向，并始终指向圆心的力叫做向心力。在图4-9中，F₁和F₂表示质点在不同位置所受的向心力。可见，受到向心力作用是质点做圆周运动的条件。

2．质点做圆周运动的条件

如果质点做圆周运动，质点一定会受到向心力的作用，这个向心力不断改变质点运动的方向，并始终沿着半径指向圆心。

点击

曲线运动

如果质点的运动轨迹是一条曲线，质点的运动就叫做曲线运动，例如运动员在弯道上奔跑、炮弹在空中的飞行等。圆周运动是曲线运动的一种。

质点做曲线远动的原因也和它的受力情况有关。当质点所受合外力不为零，而且合外力方向与质点初速度的方向不在一直线时，质点就会不断改变运动方向而做曲线运动。在各种曲线运动中，如果质点所受合外力或者合外力的某个分力始终指向一个固定的圆心，质点就可能做圆周运动；如果质点所受合外力或者合外力的某个分力没有始终指向圆心，也就是不存在向心力时，质点就做其他曲线运动。

怎样比较圆周运动的快慢？

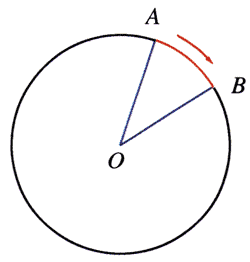
很自然，我们首先会想到用“速度”这个概念来表示圆周运动的快慢。事实上，“速度”可以表示任何质点运动的快慢，当然也可以表示质点做圆周运动的快慢。因为圆周运动的轨迹是曲线，如图4-10所示，圆周运动的速度大小要用质点所通过的 A、B 两点之间的圆弧长度s与所用时间t之比来表示，这个速度叫做线速度。

如果做圆周运动的物体线速度的大小保持不变，我们就说该物体在做匀速圆周运动。

3．圆周运动的快慢

（1）线速度（linear velocity）的大小。

质点经过的圆弧长度s与所用的时间t之比就是质点的线速度的大小。线速度用符号 v 表示，则有

v＝$\frac{s}{t}$

线速度的单位是 m/s。

线速度也有方向，怎样确定线速度的方向？

自主活动

如图4-11所示，在桌面上铺一张较大的纸，使塑料玩具陀螺在纸上转动。当陀螺转轴基本稳定时，在陀螺表面滴几滴带颜色的水，观察水在纸上留下的痕迹，你能得到什么结论？

从“自主活动”的结果可以看出，质点做圆周运动时，它在任意位置上的线速度方向，就是在该位置的切线方向，如图4-12所示。

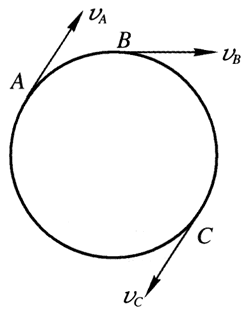
我们把线速度大小保持不变的圆周运动叫做匀速圆周运动。

（2）线速度的方向。

质点做圆周运动时，线速度的方向就是质点所在圆周位置的切线方向。

（3）匀速圆周运动（uniform circular motion）

如果做圆周运动的质点的线速度大小保持不变，或者说在相等时间内通过的圆弧长度相等，这种圆周运动就叫做匀速圆周运动。

大家谈

月球和地球谁跑得快？

图4-13中的两个天体分别是地球和月球。众所周知，月球绕地球的运动，地球绕太阳的运动，这两个运动都可看成是匀速圆周运动，关于这两个运动的快慢有着两个不同的观点。请看下面地球和月球的“对话”。

地球说：“你怎么运动得这么慢？我绕太阳运动 1 s 要走 29.79 km，你绕我运动 1 s 才走 1.02km。”

月球说：“你可别这么说！你要用一年时间才绕一个圈子，我28天就走了一圈，到底谁运动得慢。”

关于这场争论，请先谈谈你的看法。

自主活动

月球绕地球和地球绕太阳的运动都可以看成匀速圆周运动，我们来计算它们的线速度，验证地球的话是否真实。月球的轨道半径约为 3.8×10⁵km，地球的轨道半径约为 1.5×10⁸km，通过计算，看看到底谁的线速度大？

由以上计算可知，地球的线速度确实比月球的大，但是月球的话就没有任何道理吗？

如图4-14所示，当电风扇转动的时候，三个翼片的转动情况完全相同，我们可以说所有翼片转得一样快，还可以说同一翼片上的各点，也是转得一样快，尽管它们的线速度不一定相同。

可见，仅仅用线速度来描述圆周运动的快慢是不够的，还需要用与转动有关的物理量——角速度，从另一个侧面描述圆周运动的快慢。

在图4-15中，质点由 A 点沿圆周运动到B点，质点所在半径转过的角度为 φ，所用的时间为 t，用 φ 除以 t，就是质点所在半径每秒转过的角度，也就是质点的角速度的大小。角速度从另一个侧面描述了质点做圆周运动的快慢。

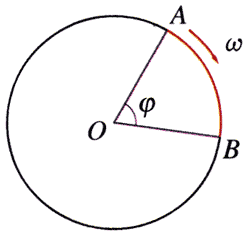
（4）角速度（angular velocity）。

当质点做圆周运动时，质点所在半径转过的角度φ和所用时间的t的比值就是角速度的大小。角速度用 ω 表示，则有

ω＝$\frac{\phi }{t}$

在国际单位制中，角度的单位是rad（弧度），时间的单位是s，角速度的单位是rad/s，读作弧度每秒。

点击

弧度

由一点出发的两条射线所夹的平面部分叫做角，角的大小叫做角度。角度的单位制有多种，常见的有六十分制和弧度制。

六十分制把圆周角分成三百六十等份，每等份就是一度，一度的六十分之一就是一分，一分的六十分之一就是一秒，分别用符号“°”“ʹ”“ʺ”表示。

弧度制规定，当圆周上的一段弧长等于该圆的半径时，该段圆弧所对的圆心角就是1弧度，弧度用符号“rad”表示，周长对应的圆心角等于2π rad，弧度也是国际单位制的角度单位。

上面两种角度单位制可以互相转换，1rad＝$\frac{{360}^{\circ }}{2\pi }$＝57°17ʹ45ʺ。

示例1

有一个质点沿半径为0.8m的圆周做匀速圆周运动，5s内通过的圆弧长度为6m，则它的线速度和角速度各为多少？

解答：根据线速度定义式有

v＝$\frac{s}{t}$＝$\frac{6}{5}$m/s＝1.2 m/s。

为求角速度，要知道5s内质点转过的角度φ，若以rad为角度的单位，则有

φ＝$\frac{s}{r}$＝$\frac{6}{0.8}$rad＝7.5rad。

再由角速度定义式有

ω＝$\frac{\phi }{t}$＝$\frac{7.5}{5}$rad/s＝1.5rad/s。

自主活动

请你分别计算出月球绕地球和地球绕太阳运动的角速度，结合前面已经计算出的地球和月球的线速度，评判地球和月球运动快慢之争。

示例2

已知地球半径为6400km。则：地球赤道上的物体随地球自转的角速度是多少？线速度是多少？

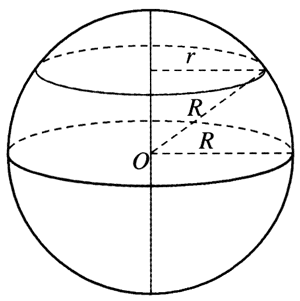
分析：前面讨论了地球的公转，本例涉及地球的自转。地球自转时，地球上所有物体都在做匀速圆周运动，它们的角速度都相同。而线速度的大小与地理纬度有关，纬度越低处，物体做圆周运动的半径r越大，如图4-16所示，线速度就越大。赤道所在的圆半径最大，赤道上物体的线速度也最大。

解答：地球自转一周，转过的角度为2π rad，所用时间为24h，由角速度公式可得

ω＝$\frac{\phi }{t}$＝$\frac{2\pi }{24\times 3600}$rad/s≈7.27×10^-5rad/s。

由线速度公式可得

v＝$\frac{2\pi R}{t}$＝$\frac{2\pi \times 6400\times {10}^3}{24\times 3600}$m/s＝465m/s。

发布时间：2016/3/17 下午3:19:14  阅读次数：4057