第七章 D 理想气体的状态方程

在海底巡航的潜艇，必须有上升到海面上的功能。潜艇上浮或下沉主要是靠艇内的水舱，舱内水面上部的空气与贮有压缩空气的贮气筒相连。潜艇若要上浮到海面，需要把筒内压缩空气压入水舱，把水舱中的水“赶”到大海中去，以减轻艇的“体重”，这样，潜艇便可上浮。如果潜艇要下沉，则需打开水舱两侧阀门，让海水进入水舱，并把空气压回贮气筒。

贮气筒内的压缩空气在水面和在水底时的压强、体积、温度都有变化。那么，这三个物理量的变化遵循什么规律呢？

一、理想气体模型

在基础型课程中，我们已经探讨过气体的实验定律。我们把能够严格地遵循气体实验定律的气体，叫做理想气体。从微观上讲，理想气体是完全忽略分子本身体积大小、完全不计分子之间相互作用力的气体。

一定质量的气体，如果温度越高、压强越小，气体就越稀薄，气体分子间距离就越大，就越接近理想气体。在温度较低、压强较大的情况下，气体不再稀薄，研究气体性质时必须考虑到分子的大小和分子间的相互作用，跟气体定律之间出现了较大的偏离，这就是必须在温度不太低、压强不太大的条件下，真实气体才能基本上遵循气体的实验定律的微观解释。

理想气体是一种理想化的物理模型，在通常温度和压强下，真实气体的性质近似于理想气体。

二、理想气体状态方程

当气体的状态发生变化时，它的状态量p（压强）、V（体积）、T（温度）往往都发生变化。现在就来研究一定质量的理想气体在状态变化中，各个状态量的变化规律。

设想在有活塞的容器内的一定质量的理想气体，在状态1时其状态量分别为p₁、V₁、T₁[图7-37（a）]；经过等温变化到中间状态c，状态量分别为p₂、V_c、T₁[图7 - 37（b）]；再经过一个等压变化过程到状态2，其状态量分别为p₂、V₂、T₂[图7-37（c）]。图7-38是容器内一定质量气体状态变化的p-V图线。

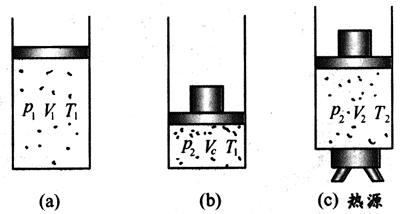
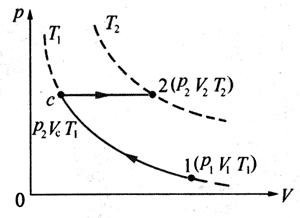
对于第一个等温过程，可根据玻意耳定律得到

p₁V₁＝p₂V_c。

对于第二个等压过程，可根据盖·吕萨克定律得到

$\frac{V_c}{T_1}$＝$\frac{V_2}{T_2}$

在以上两个式子中消去V_c，可得

$\frac{p_1{V}_1}{T_1}$＝$\frac{p_2{V}_2}{T_2}$

这就是理想气体的状态发生变化时各状态量之间的关系式，通常叫做理想气体的状态方程，简称气态方程。对于一定质量的理想气体来说，$\frac{pV}{T}$的值是个常数，即

$\frac{pV}{T}$＝C。

自主活动

通过等容过程和等温过程推导出气态方程。

示例1

有一个氢气球，在球内气体压强为1.0×10⁵Pa、温度为20℃时的体积是8m³。气球上升到高空后，在球内气体压强为0.7×10⁵Pa、温度为－50℃的条件下，该氢气球的体积有多大？

【分析】氢气球内的氢气在常压、常温下可以看作是理想气体。根据题意，其初状态的状态量分别是：p₁＝1.0×10⁵Pa，V₁＝8m³，T₁＝（273＋20）K＝293K。在高空的末状态时，各状态量分别为p₂＝0.7×10⁵Pa，T₂＝（273－50）K＝223K，则V₂可以运用气态方程求出V₂。

【解答】应用气态方程可以列出下式：

$\frac{p_1{V}_1}{T_1}$＝$\frac{p_2{V}_2}{T_2}$

即

V₂＝$\frac{p_1{V}_1{T}_2}{T_1{p}_2}$＝$\frac{1\times {10}^5\times 8\times 223}{0.7\times {10}^5\times 293}$m³≈9.1m³。

这个计算结果告诉我们，压强虽减少，但体积并没有增大多少，因为温度降低对体积变化也有影响。

由上述示例可见，应用气态方程处理问题，要注意以下几个步骤：

1．明确研究对象是哪部分气体；

2．分析气体的初、末状态之间发生了什么变化，写出各状态量的值，找出未知量；

3．根据理想气体状态方程列式；

4．统一p、V、T各状态量的单位，且T的单位必须用热力学温标单位（K），然后代入数据，算出结果。

点击

活塞式发动机是利用汽油和空气混合后在密闭的容器（气缸）内燃烧、膨胀做功。气缸里的混合气体在“压缩冲程”里，混合气体的压强增大到10个大气压，温度增加到400℃左右，其体积减小到原来的$\frac{1}{5}$～$\frac{1}{8}$。压强、温度、体积三者变化规律遵循气态方程。

示例2

在容积为40L的容器中，盛有压缩二氧化碳3.96kg，如果该容器能承受的压强不超过6.0×10⁶Pa，那么温度到达多少摄氏度时容器会有爆炸的危险？（已知二氧化碳在标准状态下的密度是1.98kg/m³）

【分析】容器内的气体在标准状态下的状态量分别是p₁＝1.0×10⁵Pa，T₁＝273K，V₁＝$\frac{m}{\rho }$＝$\frac{3.96}{1.98}$m³＝2m³；气体到达爆炸点的状态量p₂＝6.0×10⁶Pa，V₂＝40L＝0.04m³，则可运用气态方程求出T₂。

【解答】根据理想气体状态方程列式

$\frac{p_1{V}_1}{T_1}$＝$\frac{p_2{V}_2}{T_2}$

T₂＝$\frac{p_2{V}_2{T}_1}{p_1{V}_1}$＝$\frac{6.0\times {10}^6\times 273\times 0.04}{1.0\times {10}^5\times 2}$≈328K＝55℃。

由计算可知，容器温度必须控制在55℃以下，否则会引起爆炸。

【讨论】本题所给的条件中有密度这个物理量的值，若直接从密度的角度考虑，也可以解决问题。

假设标准状况下二氧化碳的密度为ρ₁，容器将爆炸时气体的密度为ρ₂，以始、末两状态时的体积V₁＝$\frac{m}{{\rho }_1}$、V₂＝$\frac{m}{{\rho }_2}$，代入气态方程

$\frac{p_{1}m}{{\rho }_1{T}_1}$＝$\frac{p_{2}m}{{\rho }_2{T}_2}$

可得到

$\frac{p_1}{{\rho }_1{T}_1}$＝$\frac{p_2}{{\rho }_2{T}_2}$

应用这个关系式，就可以直接代入数据，求出末状态时的温度

T₂＝$\frac{6.0\times {10}^6\times 273\times 1.98}{1.0\times {10}^5\times \frac{3.96}{0.04}}$K≈328K＝55℃。

发布时间：2016/2/22 下午2:02:07  阅读次数：1752