第六章 B 单摆

1581年，17岁的医学院学生伽利略在比萨教堂做弥撒时，观察到悬挂着的蜡烛架在摆动，他发现被点烛人触动了的蜡烛架摆幅会越来越小，最后慢慢停下来。伽利略暗自想，蜡烛架每次摆动的时间会不会越来越短呢？当时尚无秒表，他就用数自己脉搏的办法测量了每次摆动的时间，出乎他的意料，尽管每次摆动的摆幅越来越小，但每次摆动所用的时间却大致相同。这种摆动周期与摆动幅度无关的特性叫做摆的等时性。图6-10中就是伽利略研究摆动的比萨大教堂（右边是比萨斜塔）。回家后，他又把石头系在绳子一端重复这个实验，得到了同样结果，后来我们把这样的摆叫做单摆。有的科学史家认为以上故事可能只是个传说，但伽利略确实对摆进行了深入的研究。他还发现，对于给定的绳长，不管是用重石头还是用轻石头，摆动周期都相同。当时他正在学医，就根据这个发现设计了一种脉搏仪，用标准长度的单摆测量患者的脉搏，这是他对医学的最后一次贡献，研究单摆和其他机械装置完全改变了他的志向，他改变了在大学的学习科目，开始研究数学和科学，从此走上了科学家的道路。

一、单摆的振动过程

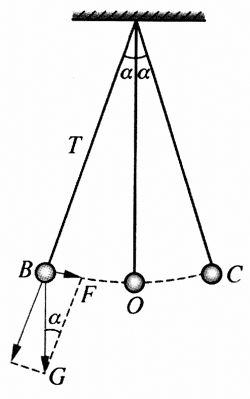
悬挂起来又能摆动的物体很多，其中最简单的就是用一根轻柔的细线悬挂一个质量比细线大得多，直径比细线长度小得多的小球，如图6-11所示，当细线的质量和小球的尺寸完全可以忽略时，我们把这样的装置叫做单摆。当然，单摆只是一个理想化的模型。

单摆为什么会振动？我们先对单摆进行受力分析，把质量为m的摆球从平衡位置O拉开一小段距离到B点，这时悬线和竖直方向的夹角为α。放开后，摆球始终受到重力mg和细线拉力T的作用。重力的一个分力F＝mgsinα沿圆弧切线方向，指向平衡位置O，而拉力T在圆弧切线方向没有分力。正是重力的分力F使摆球回到平衡位置，这个力就是使单摆振动的回复力。在平衡位置O，回复力为零，摆球依靠惯性沿圆弧继续运动，同时受到与运动方向相反的回复力的作用，于是单摆就在竖直平面里不断地沿着圆弧BC往复运动，完成了振动过程。

单摆在振动过程中，摆球的位移、速度、加速度、动能、重力势能都在不断变化。摆球的位移由平衡位置指向摆球所在位置，加速度方向始终与位移方向相反，速度方向有时与位移方向相同，有时则相反。

二、单摆的振动图象

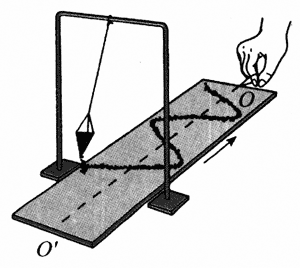
我们先用实验显示单摆的振动图象。如图6-12所示，把盛有细沙的漏斗吊在支架上，支架下方放一块硬纸板，其中间有一条直线OOʹ，漏斗静止时正好在直线OOʹ的正上方。使漏斗在垂直于OOʹ的方向上自由摆动，同时沿着OOʹ的方向匀速拉动硬纸板。因为每一时刻都有细沙从漏斗中漏出，所以落在硬纸板上的细沙就记录下各个时刻漏斗的位置，显示出一条曲线，盛有细沙的漏斗相当于单摆的摆球，这条由细沙描绘的曲线就是通过实验直接得到的单摆振动图象。在此基础上，以横轴t表示时间，以纵轴x表示位移，可以面出更加抽象和细致的单摆振动图象，如图6-13所示。这就是单摆的位移-时间图象，它描述了单摆运动的位移随时间变化的关系。

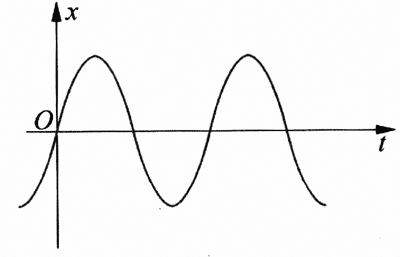
从单摆的振动图象中我们可以清楚地了解单摆振动的振幅、周期、频率以及任意时刻摆球的位移等。

自主活动

在一个盛满水的塑料瓶的底部开一个小孔，让细小水流从瓶中均匀漏出，用手中的绳吊起瓶，使其左右自由摆动，同时匀速前进，水流在地上留下的水迹也是振动图象。探究图线形状与瓶的摆动快慢、人的前进快慢有什么关系。

三、单摆的振动周期

通过探索研究，我们还可以知道单摆只有在摆角很小的情况下，它的振动周期才和振幅无关，如前所述，这种性质我们叫做单摆的等时性，那么在摆角很小的情况下，单摆做怎样的振动呢？它的周期和哪些因素有关？

自主活动

自制一个单摆，观察单摆的振动周期和振幅、摆球质量是否有关。

在图6-11中，当单摆的摆角很小（不超过5°）时，摆球的位移x和圆弧长OB很接近，设摆长为l，则

sinα≈α≈\(\frac{x}{l}\)。

于是，回复力F＝mgsinα≈mgα≈mg\(\frac{x}{l}\)＝\(\frac{{mg}}{l}\)x。

因为式中，m、g、l均为常数，可令k＝\(\frac{{mg}}{l}\)。又因为回复力F的方向指向平衡位置，始终与位移x的方向相反，于是有F＝－kx。

因此在单摆摆角α小于5°，摆球所受回复力的大小与位移成正比，方向与位移相反，可知单摆的振动是简谐运动。

荷兰物理学家惠更斯（1629－1695）研究了单摆的振动规律，发现单摆的振动周期跟摆长的平方根成正比，跟重力加速度的平方根成反比。并确定了如下单摆振动的周期公式：

T＝2π\(\sqrt {\frac{l}{g}} \)。

由于单摆的摆长和周期比较容易测定，因此可以利用单摆周期公式比较精确地测出各地的重力加速度。

大家谈

各种摆钟的摆杆和摆锤是不是单摆？它为什么可以计时？如果摆钟慢了，应如何调节？

学生实验  用单摆测定重力加速度

【实验目的】

用单摆测出当地的重力加速度。

【实验器材】

单摆、停表、直尺、直径已知的小球、铁架台等。

【实验原理】

由单摆周期公式可得

g＝4π²\(\frac{l}{{{T^2}}}\)，

测出l、T就可以计算重力加速度g。

【实验步骤】

用单摆测定重力加速度的基本步骤如下：

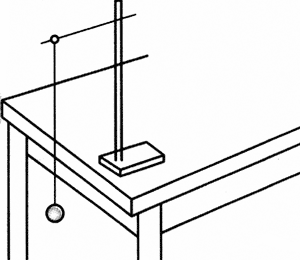
选取一个摆线长约1m的单摆，把线的上端用铁夹固定在铁架台上，把铁架台放在实验桌边，使铁夹伸到桌面以外，让摆球自由下垂，如图6-14所示。用米尺量出悬线长度l，精确到毫米，悬线长度加上小球半径就是摆长；然后放开小球让它摆动，用停表测出单摆做30～50次全振动所用的时间。计算出平均摆动一次的时间，这个时间就是单摆的振动周期。再根据单摆的周期公式，计算出重力加速度。变更摆长，重做几次实验，计算出每次实验测得的重力加速度。设计一个表格，把测得的数据和计算结果填入表中。最后，求出几次实验得到的重力加速度的平均值，即可看作本地区的重力加速度。

大家谈

在测定单摆周期时，可以从摆球通过平衡位置时开始计时，也可以从摆球到达最大位移时开始计时。你认为哪一种方法好？为什么？

本实验也可用DIS实验系统来做，其方法如下：

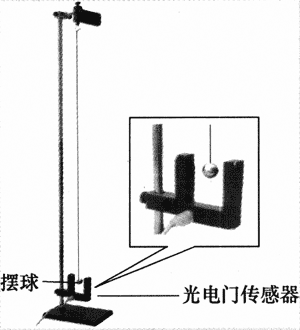
应用DIS实验系统，将图6-15中的光电传感器接到数据采集器的输入口，点击实验菜单中的“用单摆测重力加速度”。实验时，先量出摆球的半径与摆线的长度，输入计算机，单摆摆动后，点击“记录数据”，显示屏将得出一组单摆的周期与重力加速度的值。

发布时间：2016/2/7 下午10:25:33  阅读次数：2839