第四章 7 用牛顿运动定律解决问题（二）

共点力的平衡条件

桌上的书、屋顶的灯，虽然都受到力的作用，但仍保持静止。火车车厢虽然受到重力、支持力、牵引力、阻力的作用，但仍可能做匀速直线运动。如果一个物体在力的作用下保持静止或匀速直线运动状态，我们就说这个物体处于平衡状态。

受共点力作用的物体，在什么条件下才能保持平衡呢？牛顿第二定律告诉我们，当物体所受合力为0时，加速度为0，物体将保持静止或匀速直线运动状态。因此，在共点力作用下物体的平衡条件是合力为0。

例题1

城市中的路灯、无轨电车的供电线路等，经常用三角形的结构悬挂。图4.7-2为这类结构的一种简化模型。图中硬杆OB可以绕通过B点且垂直于纸面的轴转动，钢索和杆的重量都可以忽略。如果悬挂物的重量是G，角AOB等于θ，钢索OA对D点的拉力和杆OB对D点的支持力各是多大？

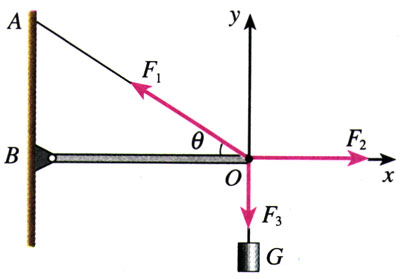
分析  分析D点受力的情况，可知它受到如图4.7-2所示的三个力的作用：钢索的拉力F₁，沿钢索方向指向A点；硬杆的支持力F₂，沿硬杆方向指向右方；悬绳的拉力F₃，方向竖直向下，大小与悬挂物的重量相等，即F₃＝G。

在平衡状态下，三个力的合力应该为0，由此可以求出F₁、F₂的大小。

解  F₁、F₂、F₃三个力的合力为0，则这三个力在任何方向的分矢量之和一定为0。我们按照图4.7-2那样建立坐标系，分别写出三个力在x方向和y方向的分矢量，于是一定有

F₂－F₁cosθ＝0    （1）

F₁sinθ－F₃＝0    （2）

由（1）（2）两式解出钢索OA的拉力F₁

F₁＝\(\frac{{{F_3}}}{{\sin \theta }}\)＝\(\frac{G}{{\sin \theta }}\)

和硬杆OB的支持力F₂

F₂＝F₁cosθ＝\(\frac{G}{{\tan \theta }}\)

当θ很小时，sinθ和tanθ都接近0，F₁和F₂就会很大，对材料的强度要求很高，所以钢索的固定点A不能距B太近。但A点过高则材料消耗过多，所以要结合具体情况适当选择θ角。

超重和失重

我们研究下面例题中描述的情境。

例题2

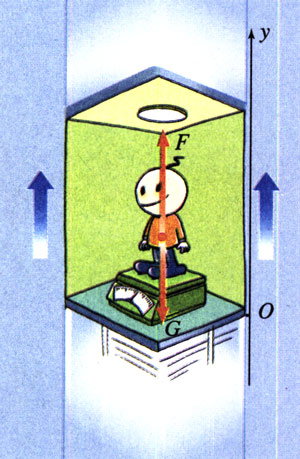
如图4.7-3，人的质量为m，当电梯以加速度a加速上升时，人对地板的压力F'是多大？

分析  人受到两个力：重力G和电梯地板的支持力F。由于地板对人的支持力F与人对地板的压力F'是一对作用力和反作用力，根据牛顿第三定律，只要求出F就可以知道F'。

电梯静止时，地板的支持力F与人所受的重力G相等，都等于mg；当电梯加速运动时，这两个力不再相等吗？

我们根据牛顿运动定律列出方程，找出几个力之间以及它们与加速度之间的关系，这个问题就能解决了。

解  沿向上的方向建立坐标轴Oy，根据牛顿第二定律写出关于支持力F、重力G、质量m、加速度a的方程

F－G＝ma

由此可得

F＝G＋ma＝m(g＋a)

人对地板的压力F'与地板支持力F的大小相等，即

F'＝m(g＋a)

由于m(g＋a)＞mg，所以当电梯加速上升时，人对电梯地板的压力比人受到的重力大。

物体对支持物的压力（或对悬挂物的拉力）大于物体所受重力的现象，称为超重（overweight）现象。

反之，电梯加速下降（或减速上升）时，加速度向下，与坐标轴的正方向相反，a是负值，所以

m(g＋a)＜mg

这时人对电梯地板的压力比人受到的重力小。

物体对支持物的压力（或对悬挂物的拉力）小于物体所受重力的现象称为失重（weightlessness）现象。如果物体正好以大小等于g的加速度竖直下落，那么a＝－g，m(g＋a)＝0，这时物体对支持物、悬挂物完全没有作用力，这种状态是完全失重状态。

从动力学看自由落体运动

在第二章，我们通过实验研究了自由落体运动，知道它是加速度的大小和方向都不变的匀变速直线运动。那时我们只分析了这个现象，没有考虑它的加速度为什么不变。要回答这个问题就要分析它的受力情况。

物体做自由落体运动有两个条件：

第一，物体是从静止开始下落的，即运动的初速度是0；

第二，运动过程中它只受重力的作用。

根据牛顿第二定律，物体运动的加速度与它受的力成正比，加速度的方向与力的方向相同。自由落体在下落的过程中所受重力的大小、方向都不变，所以加速度的大小、方向也是恒定的。

这样，学过了牛顿运动定律之后我们就可以从更高的视角审视自由落体运动了。

例题3

以10 m/s的速度从地面竖直向上抛出一个物体，空气的阻力可以忽略，分别计算0.6 s、1.6 s后物体的位置（取g＝10 m/s²）。

分析  这个物体的运动不是自由落体运动，但与自由落体相似，它在运动过程中也只受重力的作用，因此它的加速度也是g，大小、方向都不变。由于物体的初速度、加速度都是沿竖直方向的，所以它的运动不可能偏离竖直方向。结论是：这个物体在竖直方向做匀变速直线运动，可以应用匀变速直线运动的规律求解。

解  以地面为原点，竖直向上建立坐标轴（图4.7-5）。初速度的方向与坐标轴的方向一致，所以取正号，v₀＝10 m/s；加速度的方向向下，与坐标轴的方向相反，所以取负号，a＝－g＝－10 m/s²；t₁＝0.6 s，t₁＝1.6 s。

在这个问题中，物体对于原点的位移与它的坐标数值相等，因此根据匀变速直线运动的位移与时间的关系可以得到

x₁＝v₀t₁＋\(\frac{1}{2}\)at₁²

＝[10×0.6＋\(\frac{1}{2}\)×(－10)×0.6²] m＝4.2m

x₂＝v₀t₂＋\(\frac{1}{2}\)at₂²

＝[10×0.6＋\(\frac{1}{2}\)×(－10)×1.6²] m＝3.2m

抛出0.6 s后物体位于地面以上4.2 m的位置，1.6 s后位于地面以上3.2m的位置。

可能有的同学会问：一个竖直向上抛出的物体，为什么1.6 s时的位置反而比0.6 s时更低？在这个例题中，竖直向上抛出的物体不会永远向上运动。由于重力的作用，它的加速度向下，与速度方向相反，运动越来越慢，速度逐渐变为0。但是，物体不可能停在空中，它随即就会向下运动。尽管向下运动与向上运动的速度方向不同，但受力情况完全相同，所以两个运动阶段的加速度（大小、方向）也应该相同，仍是常量g。例题中算出的1.6 s时的位置，就是物体到达最高点后返回过程中所处的位置。

说一说

例题3中的物体能够到达的最大高度是多少？

提示：到达最大高度时物体的速度是0。

在得出x＝v₀t＋\(\frac{1}{2}\)at²和v²－v₀²＝2ax这两个公式时我们曾说，式中的x是物体的位移，例题3中又说x是物体的位置；两种说法有什么区别吗？实际上，讲到“位移”时，我们指的是物体离开坐标原点的位移；讲到“位置”时，指的是物体的坐标，两者的数值是相等的。 

问题与练习

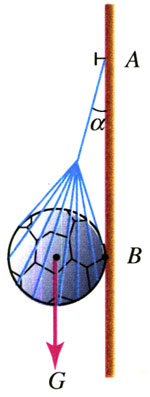
1．在光滑墙壁上用网兜把足球挂在A点，足球与墙壁的接触点为B（图4.7-6）。足球的质量为m，悬绳与墙壁的夹角为α，网兜的质量不计。求悬绳对球的拉力和墙壁对球的支持力。

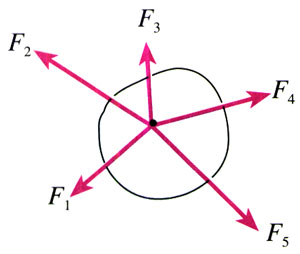
2．如图4.7-7所示，物体在五个共点力的作用下保持平衡。如果撤去力F₁，而保持其余四个力不变，请在图上画出这四个力的合力的大小和方向。

3．在饮料瓶的下方戳一个小孔，瓶中灌水，手持饮料瓶，小孔中有水喷出。放手让瓶自由下落，观察喷水的变化。解释这个现象。

4．一种巨型娱乐器械可以使人体验超重和失重。一个可乘十多个人的环形座舱套装在竖直柱子上，由升降机送上几十米的高处，然后让座舱自由落下。落到一定位置时，制动系统启动，到地面时刚好停下。已知座舱开始下落时的高度为76 m，当落到离地面28 m的位置时开始制动，座舱均匀减速。若座舱中某人用手托着重50 N的铅球，当座舱落到离地面50 m的位置时，手的感觉如何？当座舱落到离地面15 m的位置时，手要用多大的力才能托住铅球？

发布时间：2016/1/27 下午7:17:30  阅读次数：1748