第四章 6 用牛顿运动定律解决问题（一）

牛顿第二定律确定了运动和力的关系，使我们能够把物体的运动情况与受力的情况联系起来。因此，它在许多基础科学和工程技术中都有广泛的应用。由于我们目前知识的局限，这里只通过一些最简单的例子做些介绍。

从受力确定运动情况

如果已知物体的受力情况，可以由牛顿第二定律求出物体的加速度，再通过运动学的规律确定物体的运动情况。

例题1

一个静止在水平地面上的物体，质量是2 kg，在6.4 N的水平拉力作用下沿水平地面向右运动。物体与地面间的摩擦力是4.2 N。求物体在4 s末的速度和4 s内发生的位移。

分析  这个问题是已知物体受的力，求它运动的速度和位移。

先考虑两个问题。

（1）物体受到的合力沿什么方向？大小是多少？

（2）这个题目要求计算物体的速度和位移，而我们目前只能解决匀变速运动的速度和位移。物体的运动是匀变速运动吗？

解决了这两个问题之后，就可以根据合力求出物体的加速度，然后根据匀变速运动的规律计算它的速度和位移。

解  分析物体的受力情况。

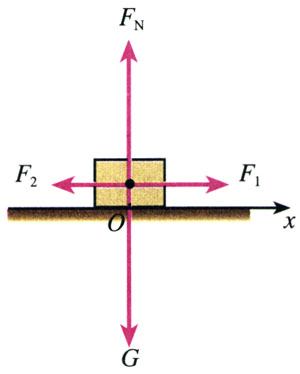
物体受到4个力的作用（图4.6-1）：拉力F₁，方向水平向右；摩擦力F₂，水平向左；重力G，竖直向下；地面的支持力F_N，竖直向上。

物体在竖直方向没有发生位移，没有加速度，所以重力G相支持力F_N大小相等、方向相反，彼此平衡，物体所受的合力等于水平方向的拉力F．与摩擦力F₂的合力。取水平向右的方向为坐标轴的正方向，则合力F＝F₁－F₂＝6.4 N－4.2 N＝2.2 N，合力的方向是沿坐标轴向右的。

物体原来是静止的，初速度为0，在恒定的合力作用下产生恒定的加速度，所以物体做初速度为0的匀加速直线运动。

由牛顿第二定律F＝ma可求出加速度

a＝\(\frac{F}{m}\)＝ \(\frac{{2.2}}{2}\)m/s²＝1.1 m/s²

求出了加速度a，由运动学公式就可以求出4 s末的速度v和4 s内发生的位移x

v＝at＝1.1×4 m/s＝4.4 m/s

x＝\(\frac{1}{2}\)at²＝\(\frac{1}{2}\)×1.1×16 m＝8.8 m

从运动情况确定受力

如果已知物体的运动情况，根据运动学公式求出物体的加速度，再根据牛顿第二定律就可以确定物体所受的力。这是力学所要解决的又一方面的问题。

例题2

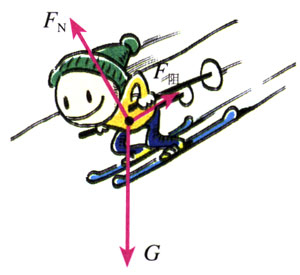
一个滑雪者，质量m＝75 kg，以v₀＝2 m/s的初速度沿山坡匀加速滑下，山坡的倾角θ＝30°，在t＝5 s的时间内滑下的路程x＝60 m，求滑雪者受到的阻力（包括摩擦力和空气阻力）。

分析  这个题目是已知人的运动情况，求人所受的力。应该注意三个问题。

（1）分析人的受力情况，按题意作草图如图4.6-2，然后考虑下面几个问题。

滑雪者共受到几个力的作用？这几个力各沿什么方向？它们之中哪个力是待求的？哪个力实际上是已知的？

（2）根据运动学的关系得到下滑加速度，求出对应的合力，再由合力求出人受的阻力。

（3）适当选取坐标系，使运动正好沿着一个坐标轴的方向。

解  如图4.6-3建立直角坐标系，把重力G沿x轴和y轴的方向分解，得到

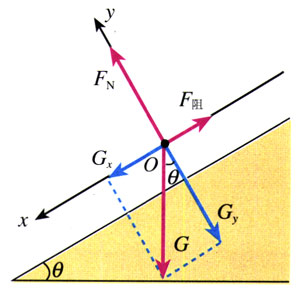
G_x＝mgsinθ

G_y＝mgcosθ

在与山坡垂直的方向，物体没有发生位移，没有加速度，所以G_y与支持力F_N大小相等、方向相反，彼此平衡，物体所受的合力F等于G_x与阻力F_阻的合力。

由于沿山坡向下的方向为正方向，所以合力F＝G_x－F_阻，合力的方向沿山坡向下，使滑雪者产生沿山坡向下的加速度。滑雪者的加速度可以根据运动学的规律求得，即由x＝v₀t＋\(\frac{1}{2}\)at²解出

a＝\(\frac{{2(x - {v_0}t)}}{{{t^2}}}\)

把已知量的数值代入，可得滑雪者的加速度

a＝4 m/s²

下面求滑雪者受到的阻力。

根据牛顿第二定律，F＝ma，因此有

G_x－F_阻＝ma

由此解出阻力

F_阻＝G_x－ma＝G_x＝mgsinθ－ma

代入数值后，得

F_阻＝67.5 N

滑雪者受到的阻力是67.5 N。

问题与练习

1．一个原来静止的物体，质量是2 kg，受到两个大小都是50 N且互成60°角的力的作用，此外没有其他的力。3 s末这个物体的速度是多大？3 s内物体发生的位移是多少？

2．以15 m/s的速度在水平路面行驶的无轨电车，在关闭电动机后，经过10 s停了下来。电车的质量是4.0×10³ kg，求电车所受的阻力。

3．民航客机一般都有紧急出口，发生意外情况的飞机紧急着陆后，打开紧急出口，狭长的气囊会自动充气，生成一条连接出口与地面的斜面，人员可沿斜面滑行到地上。若机舱口下沿距地面3.2 m，气囊所构成的斜面长度为6.5 m，一个质量60 kg的人沿气囊滑下时所受的阻力是240 N，人滑至气囊底端时速度有多大？

4．在某城市的一条水平道路上，规定车辆行驶速度不得超过30 km/h，在一次交通事故中，肇事车是一辆卡车，量得这辆卡车紧急刹车（车轮被抱死）时留下的刹车痕迹长为7.6 m。经过测试得知这种轮胎与路面的动摩擦因数为0.7，请判断该车是否超速。

发布时间：2016/1/22 下午9:21:07  阅读次数：1635