第四章 3 牛顿第二定律

牛顿第二定律

通过上一节的探究我们已经看到，小车的加速度可能与它所受的力成正比，与它的质量成反比。大量实验和观察到的事实都能得出同样的结论，由此可以总结出一般性的规律：物体加速度的大小跟它受到的作用力成正比、跟它的质量成反比，加速度的方向跟作用力的方向相同。这就是牛顿第二定律（Newton second law）。

牛顿第二定律可以用比例式来表示，这就是

a∝\(\frac{F}{m}\)

或者

F∝ma

这个比例式也可以写成等式

F＝kma

其中k是比例系数。

实际物体所受的力往往不止一个，这时式中F指的是物体所受的合力。

力的单位

我们在初中已经知道，在国际单位制中，力的单位是牛顿。“牛顿”这个单位是怎样定义的？学过牛顿第二定律之后，这个问题就清楚了。

在17世纪，人类已经有了一些基本物理量的计量标准，但是，还没有规定多大的力作为力的单位。因此，在F＝kma这个关系式中，比例系数k的选取就有一定的任意性，只要是常数，它就能正确表示F与m、a之间的比例关系。如果选取k＝1，那么就有

F＝ma

这就是今天我们熟知的牛顿第二定律的数学表达式。当物体的质量是m＝1kg、在某力的作用下它获得的加速度是a＝1m/s²时，F＝ma ＝1kg×1m/s²＝1kg·m/s²。我们就把这个力叫做“一个单位的力”。也就是说，如果质量和加速度的单位分别用千克和米每二次方秒，力的单位就是千克米每二次方秒。后人为了纪念牛顿，把kg·m/s²称做牛顿，用符号N表示。

例题1

某质量为1100kg的汽车在平直路面试车，当达到100km/h的速度时关闭发动机，经过70 s停了下来。汽车受到的阻力是多大？重新起步加速时牵引力为2000N，产生的加速度是多大？假定试车过程中汽车受到的阻力不变。

分析  由于路面水平，汽车在竖直方向受到的重力与地面的支持力大小相等、方向相反，合力为0，所以只需要考虑汽车在水平方向的运动。在水平方向，只有牵引力和阻力，使汽车产生加速度的力是这两个力的合力。

在试车的第一阶段，已经知道初速度和末速度，可以求出加速度，进而由牛顿第二定律计算汽车受到的阻力。

阻力包括路面的摩擦力和空气的阻力。一般说来，空气阻力与车速有关，但本题做了简化，认为阻力是不变的，所以从题目所给的牵引力减去第一阶段得出的阻力就是试车的第二阶段的合力，根据牛顿第二定律就能算出汽车的加速度。

同样，因为假定汽车所受的阻力和牵引力都是不变的，所以在试车的第二阶段汽车的加速度是一定的，可以应用匀变速运动的规律。

解  沿汽车运动的方向建立坐标轴（图4.3-1、4.3-2）。

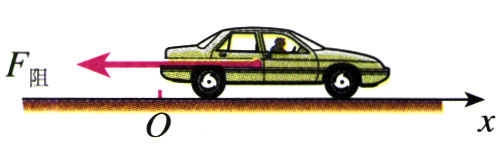
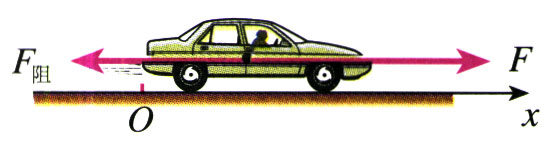
在试车的第一阶段，汽车做匀变速运动，初速度是v₀＝100 km/h＝27.8 m/s，末速度是0，滑行时间t＝70 s。因此加速度a₁为

a₁＝\(\frac{{0 - {v_0}}}{t}\)＝－\(\frac{{{v_0}}}{t}\)

汽车受到的阻力为

F_阻＝ma₁＝－\(\frac{{ m{v_0}}}{t}\)＝－\(\frac{{1100{\rm{kg}} \times 27.8{\rm{m/s}}}}{{70{\rm{s}}}}\)＝－437\(\frac{{{\rm{kg}} \cdot {\rm{m}}}}{{{{\rm{s}}^2}}}\)＝－437 N

负号表示阻力的方向与坐标轴的方向相反，即与速度的方向相反。

在重新起步并加速后，汽车除了受到上述阻力外，还受到牵引力F，F的方向与坐标轴的方向一致，取正号。合力是牵引力与阻力的代数和，即

F_合＝2000N－437N＝1563N

由牛顿第二定律可得汽车的加速度a₂

a₂＝\(\frac{{{F_合}}}{m}\)＝\(\frac{{1563{\rm{N}}}}{{1100{\rm{kg}}}}\)＝1.42 \(\frac{{\rm{N}}}{{{\rm{kg}}}}\)＝1.42 \(\frac{{{\rm{kg}} \cdot {\rm{m/}}{{\rm{s}}^2}}}{{{\rm{kg}}}}\)＝1.42 m/s²

在试车的第二阶段，加速度为正值，这表示它的方向与坐标轴的方向相同，即与速度的方向相同。

例题2

光滑水平桌面上有一个物体，质量是2 kg，受到互成120°角的两个水平方向的力F₁和F₂的作用，两个力的大小都是10N。这个物体的加速度是多大？

分析  考虑下面几个小问题有助于解决这个例题。

（1）这个问题是求物体的加速度，自然会想到由牛顿第二定律F＝ma可以得到a＝\(\frac{F}{m}\)。但是，这个问题中作用在物体上的力有F₁和F₂，还有重力和桌面对它的支持力。应该怎样计算它们的合力？

（2）物体在竖直方向并无运动，它在竖直方向所受的重力和桌面对它的支持力应该大小相等、方向相反，矢量和为0。所以，只考虑水平（桌面）方向几个力的合力就可以了。又因为桌面是光滑的，可以忽略摩擦阻力，所以只求F₁、F₂的合力即可。

（3）F₁、F₂不在一条直线上，求它们的合力时可以把两个力在各个坐标轴上的投影分别相加。这时，恰当地选择坐标轴的方向能够使问题简化。在这个问题中，应该怎样建立坐标系？

解  先求F₁和F₂的合力F_合，然后用牛顿第二定律求出加速度。

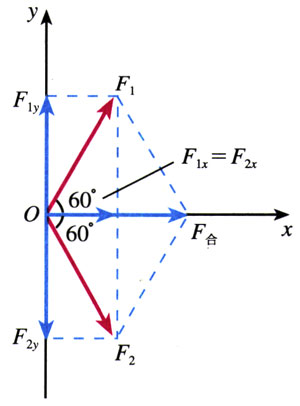
以F₁和F₂为邻边作出平行四边形。由于F₁和F₂的大小相等，由对称性可以知道，合力的方向不会偏向于F₁，也不会偏向于F₂，它应该在F₁和F₂的夹角的平分线上。所以最好以合力的方向为x轴的方向，即按图4.3-3建立坐标系。

把力F₁和F₂分别沿x轴和y轴的方向分解，它们的分力为

F_1x＝F₁cos 60°，F_1y＝F₁sin 60°

F_2x＝F₂cos 60°，F_2y＝F₂sin 60°

F₁和F₂在y方向的两个分力F_1y和F_2y大小相等、方向相反，作用相互抵消，它们在x方向的分力F_1x和F_2x的方向相同；所以F_1x和F_2x的合力就是F₁和F₂的合力，即

F_合＝F_1x＋F_2x＝F₁cos 60°＋F₂cos 60°＝5 N＋5 N＝10 N

由于知道了合力F_合与物体的质量m，由牛顿第二定律F_合＝ma就可以求出加速度

a＝\(\frac{{{F_合}}}{m}\)＝\(\frac{{10{\rm{N}}}}{{2{\rm{kg}}}}\)＝5 \(\frac{{{\rm{kg}} \cdot {\rm{m/}}{{\rm{s}}^2}}}{{{\rm{kg}}}}\)＝5 m/s²

加速度的方向与F_合方向相同，即沿F₁、F₂的角平分线方向。

说一说

质量不同的物体，所受的重力不一样，它们自由下落时加速度却是一样的。你怎样解释？

科学漫步

用动力学方法测量质量

大家都知道，质量可以用天平来测量。可是在宇宙空间，怎样测质量？设想，你自己就是一艘带有喷气发动机的飞船，你用力推一个质量未知的物体，当用力一定时，它的质量越大，产生的加速度就越小……如道了所用的力和物体的加速度，根据牛顿第二定律就能得出物体的质量了。这就是动力学的方法。飞船的推力是已知的，飞船的加速度应该怎样测出？

在阅读下面一段前请先想一想，用这种方法测量一个物体的质量，例如一个小型空间站的质量，需要进行哪些测量，测量数据应该怎样处理。方法要尽可能简单、可行。

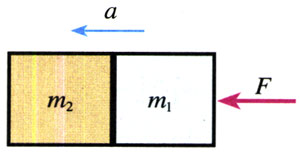
1966年曾在地球的上空完成了以牛顿第二定律为基础的测定质量的实验。实验时，用双子星号宇宙飞船m₁去接触正在轨道上运行的火箭组m₂（后者的发动机已熄火）。接触以后，开动双子星号飞船的推进器，使飞船和火箭组共同加速（图4.3-4）。推进器的平均推力F等于895 N，推进器开动时间为7 s。测出飞船和火箭组的速度变化是0.91 m/s。双子星号宇宙飞船的质量是已知的，m₁＝3 400 kg，我们要求的是火箭的质量m₂。

接下来的计算请同学们自己完成。

实际上，火箭组的质量m₂已经事先测出，为3 660 kg，与动力学方法测得的结果相差不到5%，正在预期的误差范围之内。这次实验的目的是要发展一种技术，找出测定轨道中人造天体的质量的方法。

问题与练习

1．从牛顿第二定律知道，无论怎样小的力都可以使物体产生加速度，可是，我们用力提一个很重的箱子，却提不动它。这跟牛顿第二定律有没有矛盾？应该怎样解释这个现象？

2．一个物体受到F₁＝4N的力，产生a₁＝2m/s²的加速度，要使它产生a₂＝6m/s²的加速度，需要施加多大的力？

3．甲、乙两辆实验小车，在相同的力的作用下，甲车产生的加速度为1.5m/s²，乙车产生的加速度为4.5 m/s²，甲车的质量是乙车的几倍？

4．光滑水平桌面上有一个质量是2kg的物体，它在水平方向上受到互成90°角的两个力的作用，这两个力都是14N。这个物体加速度的大小是多少？沿什么方向？

5．水平路面上质量是30kg的手推车，在受到60N的水平推力时做加速度为1.5m/s²的匀加速运动。如果撤去推力，车的加速度是多少？

发布时间：2016/1/15 上午10:43:09  阅读次数：1512