第三章 5 力的分解

力的分解

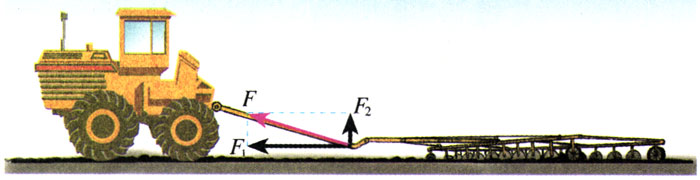
拖拉机拉着耙，对耙的拉力F是斜向上方的（图3.5-1）。与此同时，耙还受到重力和泥土对它的作用力（图中没有画出）。在这些力的共同作用下，耙沿水平方向前进。

为了分析和解决问题，例如研究耙的运动情况和它在泥土中陷入的深度，就要在水平和竖直两个方向上分别进行讨论。这时可以用图中水平方向的作用力F₁和竖直方向的作用力F₂来代替拉力F的作用。力F₁和F₂就是力F的分力。

已知一个力求它的分力的过程，叫做力的分解（resolution of force）。

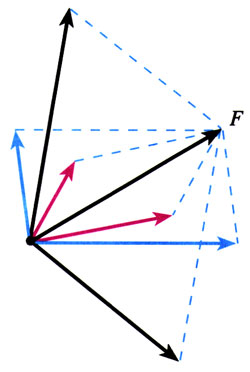
因为分力的合力就是原来被分解的那个力，所以力的分解是力的合成的逆运算，同样遵守平行四边形定则。把一个已知力F作为平行四边形的对角线，那么，与力F共点的平行四边形的两个邻边，就表示力F的两个分力。在图3.5-1中，F₁和F₂由平行四边形的两个邻边代表。需要指出的是，如果没有限制，对于同一条对角线，可以作出无数个不同的平行四边形（图3.5-2）。也就是说，同一个力F可以分解为无数对大小、方向不同的分力。一个已知力究竟应该怎样分解，要根据实际情况确定。

例题

把一个物体放在倾角为θ的斜面上。物体受到重力，大小为G，方向竖直向下，如图3.5-3甲（物体还受到其他力的作用，图中没有画出）。现在需要沿平行于斜面的方向和垂直于斜面的方向对物体的运动分别进行研究，为此建立直角坐标系如图乙。现在把重力G沿两个坐标轴的方向分解为F₁和F₂，求两个分力的大小。

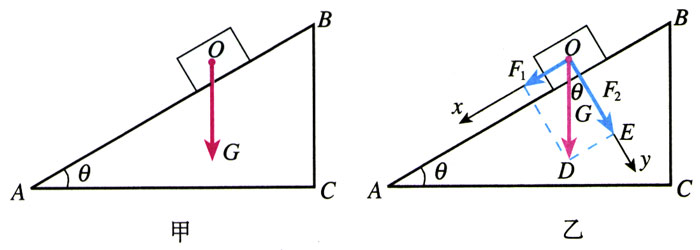
分析       由于坐标轴的方向跟斜面方向有确定的关系，因此可以找到代表力的矢量图与斜面实物图之间的几何关系。具体来说：表示重力G的线段OD跟水平面AC垂直；表示分力F₂的线段OE跟斜面AB垂直。由于斜面倾角∠BAC=θ，所以∠DOE=θ。这样，根据直角三角形中的三角函数关系便可以求出F₁和F₂的大小。

解          由以上分析可知，两个分力的大小为

F₁＝Gsinθ

F₂＝Gcosθ

可以看出，F₁和F₂的大小都与斜面的倾角有关：斜面倾角θ增大时，F₁增大，F₂减小。

一座大桥的引桥就是一个斜面。上桥时，车辆所受重力的分力F₁与运动方向相反，阻碍车辆前进；下桥时分力F₁与运动方向相同，使车辆运动加快。为了便于行车，高大的桥要造很长的引桥，以减小斜面的倾角。

矢量相加的法则

力是矢量，求两个力的合力时，不能简单地把两个力的大小相加，而要按平行四边形定则来确定合力的大小和方向。

我们曾经学过位移，它也是矢量。如图3.5-5，一个人从A走到B，发生的位移是AB，又从B走到C，发生的位移是BC。在整个运动过程中，这个人的位移是AC，AC是合位移。

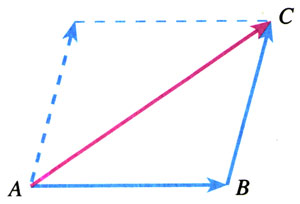
在图3.5-5中，如果平行地移动矢量BC，使它的始端B与第一次位移的始端A重合，于是我们看到，两次位移构成了一个平行四边形的一组邻边，而合位移正是它们所夹的对角线。所以说，位移矢量相加时也遵从平行四边形定则。

从另一个角度看，图3.5-5中AB和BC两个位移与它们的合位移AC组成一个三角形。像这样把两个矢量首尾相接从而求出合矢量的方法，叫做三角形定则（triangular rule）。三角形定则与平行四边形定则的实质是一样的。

既有大小又有方向，相加时遵从平行四边形定则（或三角形定则）的物理量叫做矢量（vector）。只有大小，没有方向，求和时按照算术法则相加的物理量叫做标量（scalar）。

说一说

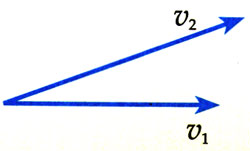
如图3.5-6，一个物体的速度v₁在一小段时间内发生了变化，变成了v₂。你能根据v₁、v₂，按照矢量相加的法则找出变化量Δv吗？

在第一章第5节，我们曾针对直线运动的速度，通过作图讨论过两个矢量v₁、v₂与它们的变化量Δv之间的关系。当时曾经指出：以原来的速度v₁的箭头端为起点，以后来的速度v₂的箭头端为终点，作出一个新的箭头，它就表示速度的变化量Δv。由于Δv＝v₁－v₂，所以这个方法实际上是求两个矢量之差的一般性方法。

现在的问题是，图3.5-6中的v₁、v₂不在同一条直线上，还能应用这个方法吗？回答是肯定的。把Δv＝v₁－v₂稍稍变形，根据矢量相加的法则，你自己就能证明这一点。

问题与练习

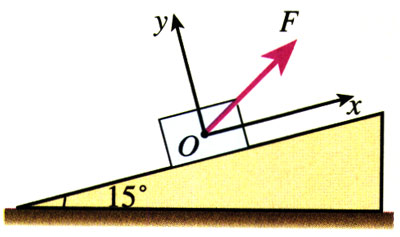
1．如图3.5-7，倾角为15º的斜面上放着一个木箱，100 N的拉力F斜向上拉着木箱，F与水平方向成45º角。分别以平行于斜面和垂直于斜面的方向为x轴和y轴建立坐标系，把F分解为沿着两个坐标轴的分力。试在图中作出分力F_x和F_y，并计算它们的大小。

2．一个竖直向下的180 N的力分解为两个分力，一个分力在水平方向上并等于240 N，求另一个分力的大小和方向。

3．一个小球在1 s时间内在水平方向上向右发生了4 m位移，同在这1 s内，它也下落了5 m。作图表示这个小球位移的方向，计算小球位移的大小。

发布时间：2015/12/24 下午2:23:57  阅读次数：2132