第三章 4 力的合成

生活中常常见到这样的事例：如图3.4-1，一个力的作用效果与两个或者更多力的作用效果相同。

当一个物体受到几个力的共同作用时，我们常常可以求出这样一个力，这个力产生的效果跟原来几个力的共同效果相同，这个力就叫做那几个力的合力（resultant force），原来的几个力叫做分力（components of force）。

力的合成

求几个力的合力的过程叫做力的合成（composition of forces）。这里我们探究求几个力的合力的方法。

思考与讨论

在图3.4-1中，假如这桶水的重量是200 N，两个孩子合力的大小一定也是200 N。现在问题是：如果两个孩子用力的大小分别是F₁和F₂，F₁和F₂两个数值相加正好等于200 N吗？

实验

探究求合力的方法

如图3.4-2甲，轻质小圆环挂在橡皮条的下端，橡皮条的长度为GE。

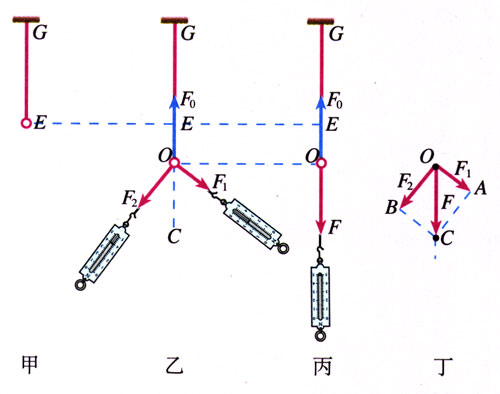
在图乙中，用手通过弹簧测力计拉动小圆环，小圆环受到作用力F₁、F₂，橡皮条伸长，小圆环处于O点。这时它还受到橡皮条对它向上的拉力F₀[1]。

撤去F₁、F₂，改用一个力F拉住小圆环，仍使它处于O点（图丙）。

对于小圆环来说，力F的作用效果与F₁、F₂共同作用的效果是一样的，也能够与橡皮条对它的拉力F₀平衡，所以F等于F₁、F₂的合力。

我们要探究的是：合力F与分力F₁、F₂有什么关系？

探究时要注意下面几个问题。

1．F₁、F₂、F的方向是沿着几条拉线方向的，因此要把拉线的方向描在木板的白纸上。

2．F₁、F₂、F的大小由弹簧测力计读出，用力的图示法在纸上画出表示几个力的箭头。

3．怎样表述合力的大小、方向与分力的大小、方向的关系？

建议用虚线把合力的箭头端分别与两个分力的箭头端连接，也许能够得到启示。

4．得出你的结论后，改变F₁和F₂的大小和方向，重做上述实验，看看结论是否相同。

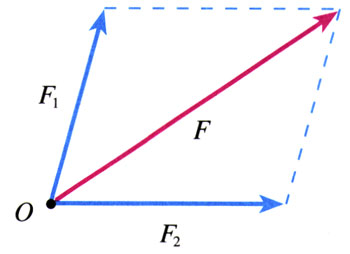
两个力合成时，以表示这两个力的线段为邻边作平行四边形，这两个邻边之间的对角线就代表合力的大小和方向（图3.4-3）。这个法则叫做平行四边形定则（parallelogram rule）。

例题

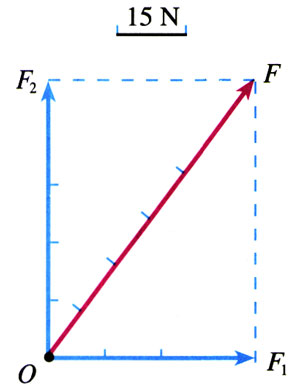
力F₁＝45 N，方向水平向右。力F₂＝60 N，方向竖直向上。通过作图求这两个力的合力F的大小和方向。

分析与解      选择某一标度，例如用8 mm长的线段表示15 N的力，作出力的平行四边形，如图3.4-4所示，表示F₁的线段长24 mm，表示F₂的线段长32 mm。

用刻度尺测量后得知，表示合力F的对角线长40 mm，所以合力的大小F＝15 N×＝75 N。

用量角器量得合力F与力F₁的夹角为53º。

如果两个以上的力作用在一个物体上，也可以应用平行四边形定则求出它们的合力：先求出任意两个力的合力，再求出这个合力跟第三个力的合力，直到把所有的力都合成进去，最后得到的结果就是这些力的合力。

思考与讨论

根据力的平行四边形定则作图。可以看出，两个力F₁、F₂的合力F的大小和方向随着F₁、F₂的夹角而变化。当夹角分别等于0º和180º时，怎样确定合力F的大小与方向？

共点力[2]

如果一个物体受到两个或更多力的作用，有些情况下这些力共同作用在同一点上，或者虽不作用在同一点上，但它们的延长线交于一点，如图3.4-5，这样的一组力叫做共点力（concurrent forces）。另一些情况下，这些力不但没有作用在同一点上，它们的延长线也不能交于一点，如图3.4-6，这一组力就不是共点力。

力的合成的平行四边形定则，只适用于共点力。

问题与练习

1．有两个力，一个是10 N，一个是2 N，它们的合力有可能等于5 N、10 N、15 N吗？合力的最大值是多少？最小值是多少？

2．有两个力，它们的合力为0。现把其中一个向东的6 N的力改为向南（大小不变），它们的合力大小、方向如何？

3．两个力互成30º角，大小分别是90 N和120 N。通过作图求出合力的大小和方向。如果这两个力的大小不变，两力间的夹角变为150º，通过作图求出合力的大小和方向。

4．两个力F₁和F₂间的夹角为θ，两力的合力为F。以下说法是否正确？

（1）若F₁和F₂大小不变，θ角越小，合力F就越大。

（2）合力F总比分力F₁和F₂中的任何一个力都大。

（3）如果夹角θ不变，F₁大小不变，只要F₂增大，合力F就必然增大。

发布时间：2015/12/23 下午3:57:46  阅读次数：1639