第五章 A 向心加速度 向心力

本章将在学习基础型课程有关圆周运动初步知识的基础上，进一步探究物体做圆周运动的原因；建立向心加速度概念；探究向心力和哪些因素有关，加深对力和运动变化关系的理解；感受“以直代曲”的极限思想；了解圆周运动的实际应用。同时，还要学习离心现象，感悟生活语言和科学概念的区别，学习用科学知识来认识和描述自然现象。

链球的话：“我是田径比赛用的链球，球体的质量约7.26kg，直径约12.9cm，链和球的全长约117～121cm，人们制造我，是为了开展投掷运动。我的祖先可没有我这样漂亮，只是一把长柄铁锤，矿工们在休息时比赛谁能把铁锤扔得更远，图5-1描绘了当时的情形，后来才发展为现在的链球运动。因为我质量较大，要想把我抛得很远可没有那么容易，非得训练有素的链球运动员才行，男子链球的世界纪录是86.75m。你一定会感到吃惊，这么重的东西居然能抛得这么远！我只是个链球，不懂什么道理，也说不清运动员怎么能把我抛得这么远。我只知道运动员先要用尽全身的力气，像图5-2所示那样拉住钢链使我沿着圆周转几图，用的力越大，转得就越快，最后，凭他们的技巧，在规定的方向上把我抛得远远的。你们都是聪明的学生，通过学习后一定比我更明白：我为什么会做圆周运动？运动员又是如何控制方向的？我想，同样的道理在铁饼运动员的身上也可以得到体现。”

图5-3中所示的“水流星”是我国传统的杂技节目，演员们把盛有水的容器用绳子拉住在空中如流星般快速舞动，同时表演高难度的动作，容器中的水居然一滴也不掉下来。

下面我们先完成“自主活动”，然后思考两个问题。

（1）“水流星”的运动快慢与手中力的大小有什么关系？

（2）如果手中的力渐渐减小，将会发生什么现象？

大家谈

看了链球的自述，我们先议论一下，猜想：链球为什么会做圆周运动？怎样才能把链球抛得很远？

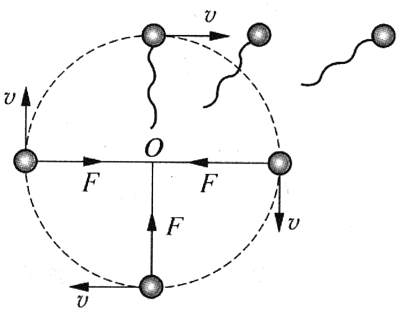
根据牛顿第一定律，可以判断质点如保持静止或做匀速直线运动，质点将不受外力作用（或所受合外力为零）。质点做圆周运动，当然既不是保持静止，也不是做匀速直线运，必然受外力作用，我们的体验也确实如此。这个外力总是使物体速度变化的方向指向圆心，或者说这个力总是指向圆心，如图5-4所示，我们把这个力叫做向心力。

自主活动

我们也做一个“水流星”的实验，来体会物体做圆周运动的条件。

在一个空的小金属食品罐的沿口处打两个小孔，再用长1m左右、强韧的尼龙绳穿过小孔缚牢，在罐中注入适量的水，拉住绳的另一端使食品罐在空中做圆周运动，体验怎样使水不流出来。

一、向心力

使质点做匀速圆周运动的力叫做向心力，向心力的方向永远指向圆心，和质点速度方向垂直，向心力不改变质点速度大小，只改变速度方向。

1．向心力与哪些因素有关

探索研究

下面我们用DIS实验来探究：向心力与哪些因素有关？有什么关系？

探究的基本思路是运用控制变量法，对有关变量进行测量，再对数据进行分析，得出结论。

所用的实验仪器叫做“DIS向心力实验器”，如图5-5所示。

大致步骤分为：

（1）分组讨论，猜想向心力与哪些因素有关。

（2）熟悉向心力实验仪，了解操作及读数要领。

（3）控制其他物理量不变，测量并记录向心力与某个物理量的有关数据。

（4）整理数据，得出结论。

由实验探究所记录的数据，经过分析可得出结论：

______________________________________________________。

2．向心力公式

由实验结果可得    F＝mω²r。

式中F表示向心力，m表示物体的质量，ω表示角速度，r表示圆周半径。应用线速度v和角速度的关系，向心力公式还可以表示为

F＝m\(\frac{{{v^2}}}{r}\)。

大家谈

在前一阶段学习牛顿第二定律后，我们已经知道，物体如果受到力的作用，且合力不为零，它一定具有加速度，那么做匀速圆周运动的物体，受到向心力的作用，它有没有加速度？如果有加速度为什么它的速度大小不变？

二、向心加速度

向心加速度表示做匀速圆周运动的质点速度方向变化的快慢。向心加速度的方向和向心力的方向一致，始终指向圆心。

自主活动

请你根据牛顿第二定律，由向心力公式推出向心加速度公式。

通过前面的“自主活动”可得出向心加速度公式：

a＝ω²r＝\(\frac{{{v^2}}}{r}\)＝\(\frac{{4{\pi ^2}}}{{{T^2}}}\)r。

式中T为物体做圆周运动的周期。

示例1

要使一个质量为3kg的物体，在半径为2m的圆周上以4m/s的速度做匀速圆周运动，物体的向心加速度和所需向心力是多少？

【分析】由已知的线速度和半径可求向心加速度，由已知质量根据牛顿第二定律可计算向心力。

【解】由向心加速度公式可得

a＝\(\frac{{{v^2}}}{r}\)＝\(\frac{{{16}}}{2}\)m/s²＝8m/s²。

由牛顿第二定律可得

F＝ma＝3×8N＝24N。

拓展联想

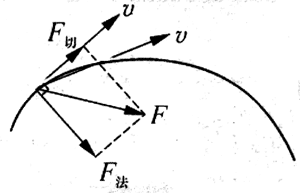
做任意曲线运动的质点，其速度大小和方向都可以改变。它受到的合力可以按切向和法向（与轨迹相切的方向和与切线垂直的方向）进行分解，如图5-6所示，切向力改变速度的大小，法向力改变速度的方向，圆周运动中的法向力就是向心力。

示例2

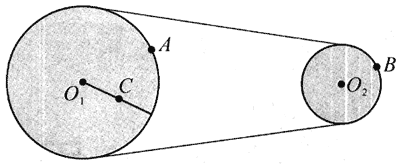
图5-7中O₁、O₂两轮通过皮带传动，两轮半径之比r₁∶r₂＝2∶1，点A在O₁轮边缘上，点C在O₁轮半径中点，点B在O₂轮边缘上，请填写A、B、C三点的线速度之比、角速度之比和加速度之比。

（1）线速度之比：v_A∶v_B∶v_C＝__________。

（2）角速度之比：ω_A∶ω_B∶ω_C＝__________。

（3）加速度之比：a_A∶a_B∶a_C＝__________。

【分析】通过皮带或链条传动的两轮轮缘的线速度应该相等，同一轮各点的角速度都相等，同一轮各点的线速度与该点到圆心的半径成正比。

【解】（1）v_A应等于v_B，vc则是v_A的二分之一，所以

v_A∶v_B∶v_C＝2∶2∶1。

（2）ω_A应等于ω_C，ω_B是ω_A 的2倍，所以

ω_A∶ω_B∶ω_C＝1∶2∶1。

（3）因为a＝\(\frac{{{v^2}}}{r}\)＝ω²r，由以上解答，可得

a_A∶a_B∶a_C＝2∶4∶1。

自主活动

找出下列现象中向心力的来源。

1．汽车转弯。图5-8表示汽车转弯时，轮胎形变的情况。（轮胎下部向左突出）

2．公交车内站立着的乘客随车转弯。

3．儿童乐园内坐在旋转木马上的儿童转弯。

发布时间：2015/10/29 下午2:23:19  阅读次数：3384