B 机械能守恒定律的应用

机械能守恒定律在人们的日常生活和生产技术中有广泛的应用，当然是近似地应用。图4-7是游乐场中的“荡船”，它向左右两边可以摆起很高，抵达最低位置时速度很大，游客感到惊险又刺激，不考虑摆动过程中的摩擦等阻力因素，可以认为它是机械能守恒定律的一种应用。图4-8是我国云南罗平九龙瀑布的英姿。群山环绕，瀑姿优雅。它共有10级，最壮观的“神龙瀑”，落差达56m，宽112m．年平均流量为18.13m/s。

如果不计空气阻力，水下落时也是遵循机械能守恒定律的，我们可以应用该定律求出水落到瀑布底部时每秒钟获得的动能。从而可估算出用这些水的全部能量来发电的功率。

本节将通过几个实例来学习有关机械能守恒定律的应用和分析计算。

应用机械能守恒定律解题的基本要点

解决有关机械能守恒的实际问题时应注意哪些步骤呢？

运用机械能守恒定律解题的过程一般包括以下几个步骤：

（1）确定研究的系统；

（2）判断是否符合机械能守恒条件；

（3）选取零势能面；

（4）确定初状态和末状态的动能和势能；

（5）写出表达式解题，得出结果。

示例1

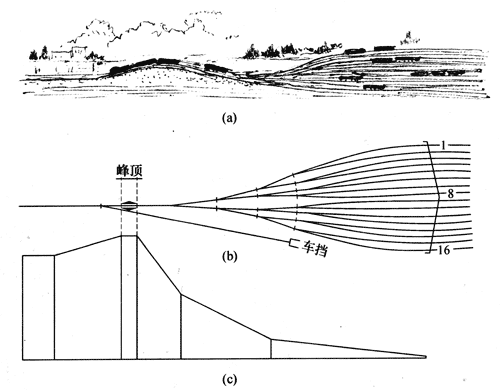
铁道上的列车车厢经常需要分类编组，图4-9（a）所示的就是常用的“驼峰”编组站，它是一种为列车提供分解车体进行编排组合各种车厢的设施。它因从侧面看酷似骆驼的背部而得名。图4-9（b）、（c）是它的俯视图和侧视图，列车大约以1.2m/s的速度倒着将车厢推至峰顶，然后脱开车钩，让车厢滑入应进入的车道，实行编组。为了防止进入编组道的车速过大，滑行途中还装有减速器。

如果车厢未经减速器，也不计阻力，它滑到底部速度是8m/s，那么驼峰的高度为多大？

【分析】本问题的研究对象是车厢，设其质量为m，不计任何阻力时只有重力做功，机械能守恒。取地面为零势能面，则车厢在驼峰时总机械能为mgh＋$\frac{1}{2}$mv₀²（h为“驼峰”高度，v₀为初速度）。抵达地面时总机能能为$\frac{1}{2}$mv²（v为末速度）。

【解答】根据机械能守恒定律，

mgh＋$\frac{1}{2}$mv₀²＝$\frac{1}{2}$mv²，

h＝$\frac{v^2-v_0^2}{2g}$＝$\frac{8^2-{1.2}^2}{2\times 10}$m＝3.1m。

即“驼峰”的高度h约为3.1m。

点击

实际上图4-9中车厢下滑的坡度（斜坡的高度与水平距离的比值）比图上所画小得多，一般是0.15%～0.35%，最陡之处也只有4%。

示例2

如图4-10所示，质量为m的A球与质量为2m的B球由轻杆相连，两球心间距离为l，放置在成直角的光滑槽内。开始时轻杆成竖直状态，两球均处于静止状态。放开后，A球沿竖直槽壁向下滑动，B球沿水平槽壁向右滑动，最终两球一起在水平槽中滑动，求两球最终速度。

【分析】本题研究对象是由轻杆相连的两个小球，运动过程中只有重力做功，其他力不做功，满足机械能守恒条件。取两球最后一起做水平运动时重心的高度为零势能位置。整个过程中只有A球势能减少了，两球初动能均为零，最终两球动能都增加了，且速度相同，可以运用“势能的减少等于动能的增加”来解题。

【解答】设两球的最终速度为v。两球的质量分别为m_A和m_B，则

m_Agl＝$\frac{1}{2}$m_Av²＋$\frac{1}{2}$m_Bv²。

因为m_A＝m，m_B＝2m，代入后可得

mgl＝$\frac{1}{2}$（m＋2m）v²，

v＝$\sqrt{\frac{2}{3}gl}$。

自主活动

相互垂直的轻杆，中央为一转动轴O，杆端固定着四个小球（如图4-12）。最高点的小球质量为2m，其余小球质量均为m，释放后发生转动，当2m球抵达最低点时，各球速度为多大？

示例3

如图4-12所示，半径为r，质量不计的圆盘盘面与地面相垂直，圆心处有一个垂直盘面的光滑水平固定轴O，在盘的最右边缘处固定一个质量为m的小球A，在O点的正下方离O点$\frac{r}{2}$处固定一个质量也为m的小球B，放开盘让其自由转动，问：

（1）A球转到最低点时线速度为多大？

（2）在转动过程中半径OA向左偏离竖直方向的最大角度是多少？

【分析】本问题研究的是两个小球组成的系统，在转动过程中，只有重力做功，可以运用机械能守恒定律。

解答问题（1）时要注意两球的线速度是不同的，任何时刻v_A＝2v_B。

解答问题（2）要注意，当OA达到最大偏角时，两球动能为零。只要运用末状态（图4-13）势能等于最初状态势能，就能解题。

【解答】（1）从图4-12状态至图4-13状态，两球势能的减少为ΔE_p＝mgr＋mg$\frac{r}{2}$－mgr＝$\frac{1}{2}$mgr（取圆盘最低处的水平面势能为零），根据机械能守恒定律，应有

$\frac{1}{2}$mgr＝$\frac{1}{2}$mv_A²＋$\frac{1}{2}$m（$\frac{v_A}{2}$）²＝$\frac{1}{2}$m·$\frac{5}{4}$v_A²，

解得       v_A＝$\sqrt{\frac{4}{5}gr}$。

（2）设圆心所在水平面势能为零，根据初始位置重力势能与图4-14状态的重力势能相等，可得到

－mg$\frac{r}{2}$＝－mgrcosθ＋mg$\frac{r}{2}$sinθ，

rcosθ－$\frac{r}{2}$（1＋sinθ）＝0，

4（1－sin²θ）＝1＋sin²θ＋2sinθ，

5sin²θ＋2sinθ－3＝0，

sinθ＝$\frac{-1\pm \sqrt{1+15}}{5}$，

sinθ＝$\frac{3}{5}$，sinθ＝－1（负根舍去），

θ＝37°。

点击

零势能位置，可根据解题方便任意选取。

选取不同的零势能位置，解得的结果是相同的。

发布时间：2015/10/23 上午8:59:50  阅读次数：2210