3 匀变速直线运动的位移与时间的关系

匀速直线运动的位移

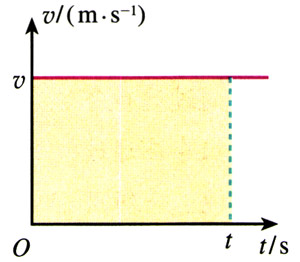
做匀速直线运动的物体在时间t内的位移x＝vt。在它的v-t图象中（图2.3-1），着色的矩形的边长正好是v和t，矩形的面积正好是vt。可见，对于匀速直线运动，物体的位移对应着v-t图象下面的面积。

对于匀变速直线运动，它的位移与它的v-t图象，是不是也有类似的关系？

思考与讨论

一次课上，老师拿来了一位往届同学所做的“探究小车的运动规律”的测量记录，表中“速度v”一行是这位同学用某种方法（方法不详）得到的物体在0，1，2，…，5几个位置的瞬时速度。原始的纸带没有保存。

以下是关于这个问题的讨论。

老师：能不能根据表中的数据，用最简便的方法估算实验中小车从位置0到位置5的位移？

学生A：能。可以用下面的方法估算：

x＝0.38×0.1＋0.63×0.1＋0.88×0.1＋1.11×0.1＋1.38×0.1＝……

学生B：这个方法不好。从表中看出，小车的速度在不断增加，0.38只是0时刻的瞬时速度，以后的速度比这个数值大。用这个数值乘以0.1 s，得到的位移要比实际位移小。后面的几项也有同样的问题。

学生A：老师要求的是“估算”，这样做是可以的。

老师：你们两个人说得都有道理。这样做的确会带来一定误差，但在时间间隔比较小、精确程度要求比较低的时候，可以这样估算。

要提高估算的精确程度，可以有多种方法。其中一个方法请大家考虑：如果当初实验时，时间间隔不是取0.1 s，而是取得更小些，比如0.06 s，同样用这个方法计算，误差是不是会小一些？如果取0.04 s，0.02 s，…误差会怎样？

欢迎大家发表意见。

匀变速直线运动的位移

按照上面讨论中提出的思想，我们通过v-t图象，研究以初速度v₀，做匀变速直线运动的物体，在时间t内发生的位移。物体运动的v-t图象如图2.3-2甲所示。

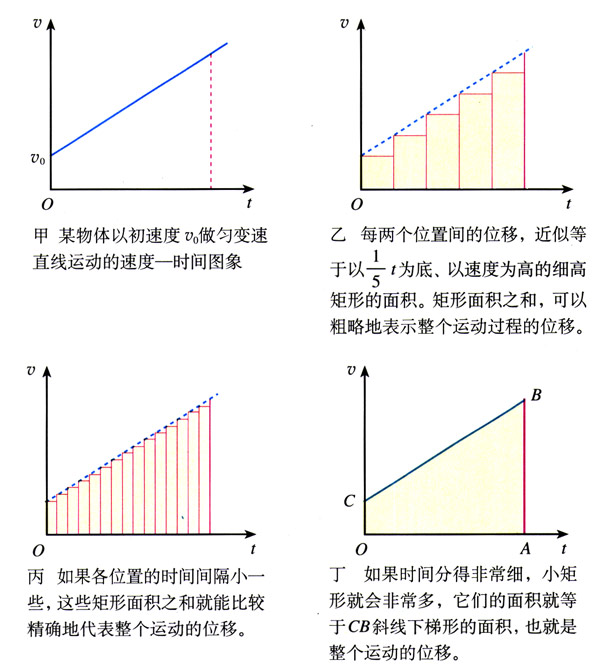
先把物体的运动分成几个小段，例如\(\frac{1}{5}\)t算一个小段，在v-t图中，每小段起始时刻物体的瞬时速度由相应的纵坐标表示（图2.3-2乙）。我们以每小段起始时刻的速度乘以时间\(\frac{1}{5}\)t，近似地当做各小段中物体的位移。在v-t图中，各段位移可以用一个又窄又高的小的面积代表。5个小矩形的面积之和近似地代表物体在整个过程中的位移。

当然，上面的做法是粗糙的。为了精确一些，可以把运动过程划分为更多的小段，如图2.3-2丙，用所有这些小段的位移之和，近似代表物体在整个过程中的位移。从v-t图象上看，就是用更多的但是更窄的小矩形的面积之和代表物体的位移。

可以想像，如果把整个运动过程划分得非常非常细，很多很多小矩形的面积之和就能非常准确地代表物体的位移了。这时，“很多很多”小矩形顶端的“锯齿形”就看不出来了，这些小矩形合在一起成了一个梯形OABC。梯形OABC的面积就代表做匀变速直线运动的物体从0（此时速度是v₀）到t（此时速度是v）这段时间间隔的位移。

请你复习：

1．怎样计算梯形的面积？

2．图2.3-2丁中，哪两条线段是梯形的底，哪两条是梯形的腰？

在图2.3-2丁中，CB斜线下梯形OABC的面积是

S＝\(\frac{1}{2}\)（OC＋AB）×OA

把面积及各条线段换成所代表的物理量，上式变成

x＝\(\frac{1}{2}\)( v₀＋v ) t

把前面已经得出的v＝v₀＋at代入，得到

x＝v₀ t＋\(\frac{1}{2}\)at²

这就是表示匀变速直线运动的位移与时间关系的公式。

如果初速度为0，这个公式简化为x＝\(\frac{1}{2}\)at²。

例题

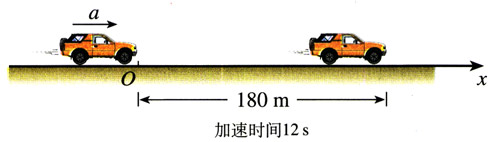
一辆汽车以1 m/s²的加速度加速行驶了12s，驶过了180 m。汽车开始加速时的速度是多少？

分析 我们研究的是汽车从开始加速到驶过180m这个过程。

以开始加速的位置为原点，沿汽车前进的方向建立坐标轴（图2.3-3）。过程结束时汽车的位移x＝180 m。由于汽车在加速行驶，加速度的方向与速度方向一致，也沿坐标轴的正方向，所以加速度取正号，即a＝1 m/s²。整个过程经历的时间是t＝12 s。汽车的运动是匀变速直线运动，待求的量是这个过程的初速度v₀。

解 由x＝v₀t＋\(\frac{1}{2}\)at²可以解出

v₀＝\(\frac{x}{t}\)－\(\frac{1}{2}\)at

把已知数值代入

v₀＝\(\frac{180m}{12s}\)－\(\frac{1}{2}\)×1 m/s²×12 s＝9m/s

汽车开始加速时的速度是9 m/s。

一般应该先用字母代表物理量进行运算，得出用已知量表达未知量的关系式，然后再把数值代入式中，求出未知量的值。这样做能够清楚地看出未知量与已知量的关系，计算也比较简便。

用图象表示位移

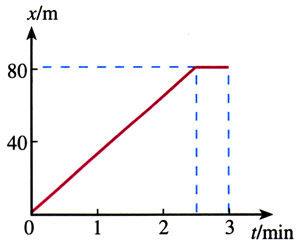
物体的位移也可以用图象描述。例如，火车的机车在沿直线轨道移动，图2.3-4描述了它对于出发点的位移随时间变化的情况，这个图象称为位移一时间图象（x-t图象）。

从图象中可以看出，在t＝0到t＝2.5 min这段时间，位移在不断增加，说明机车在远离出发点；而在t＝2.5 min和t＝3 min之间位移没有变化，总是x＝80 m，说明这段时间里机车停在距出发点80 m的位置。

这个图象是用来描述机车运动的位移与时间的关系的数学工具，机车并不是沿着这样的路线运动的。

思考与讨论

运用初中数学课中学过的函数图象的知识，你能画出初速度为0的匀变速直线运动x＝\(\frac{1}{2}\)at²的x-t图象的草图吗？

如果一位同学问：“我们研究的是直线运动，为什么你画出来的x-t图象不是直线？”你应该怎样向他解释？

问题与练习

1．A、Aʹ两个物体在做匀速直线运动，速度分别为v、vʹ（vʹ＞v），从计时开始到时刻t的位移分别为x、xʹ。

（1）写出两个物体的位移与时间的关系式。

（2）在同一个坐标系中分别作出两个物体的速度-时间图象的草图。

（3）在同一个坐标系中分别作出两个物体的位移-时间图象的草图。

2．以36 km/h速度行驶的列车开始下坡，在坡路上的加速度等于0.2 m/s²，经过30 s到达坡底，求坡路的长度和列车到达坡底时的速度。

3．以18 m/s的速度行驶的汽车，制动后做匀减速运动，在3s内前进36 m，求汽车的加速度。

4．速度、加速度的测量通常比位移的测量要复杂些，而有的时候我们只需比较两个物体运动的加速度，并不需要知道加速度的大小，例如比较两辆汽车的加速性能就是这样。如果已知两个物体在相同时间内从静止开始运动的位移之比，怎样根据运动学的规律由此求出它们的加速度之比？

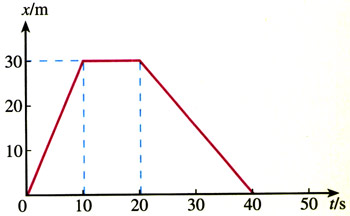
5．一辆汽车在教练场上沿着平直道路行驶，以x表示它对于出发点的位移。图2.3-5为汽车在t＝0到t＝40 s这段时间的x-t图象。通过分析回答以下问题。

（1）汽车最远距离出发点多少米？

（2）汽车在哪段时间没有行驶？

（3）汽车在哪段时间驶离出发点，在哪段时间驶向出发点？

发布时间：2015/10/10 上午9:51:25  阅读次数：1902