2 匀变速直线运动的速度与时间的关系
匀变速直线运动
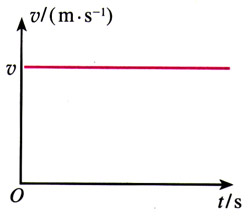
在图2.2-1中，物体运动的v-t图象是一条平行于时间轴的直线，这表示物体的速度不随时间变化，也就是说，它描述的是匀速运动。在上节的实验中，小车在重物牵引下运动的v-t图象是一条倾斜的直线，它表示小车在做什么样的运动？
从图2.2-2可以看出，由于v-t图象是直线，无论∆t选在什么区间，对应的速度v的变化量∆v与时间t的变化量∆t之比
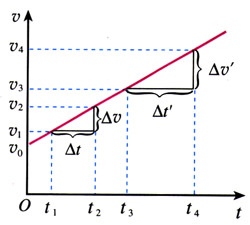
沿着一条直线，且加速度不变的运动，叫做匀变速直线运动（uniform variable rectilinear motion）。匀变速直线运动的v-t图象是一条倾斜的直线。
在匀变速直线运动中，如果物体的速度随着时间均匀增加，这个运动叫做匀加速直线运动；如果物体的速度随着时间均匀减小，这个运动叫做匀减速直线运动。
速度与时间的关系式
除图象外，还可以用公式表达物体运动的速度与时间的关系。
对于匀变速直线运动来说，由于它的v-t图象是一条倾斜的直线，无论∆t大些还是小些，对应的速度变化量∆v与时间变化量∆t之比都是一样的，因此，我们可以把运动开始时刻（t＝0）到t时刻的时间间隔作为时间的变化量，而t时刻的速度v与开始时刻的速度v0（叫做初速度，initial velocity）之差就是速度的变化量，也就是
∆t＝t－0 （1）
∆v＝v－v0 （2）
把（2）式除以（1）式，考虑到
v＝v0＋at
这就是表示匀变速直线运动的速度与时间关系的公式。
物理学中所说的加速运动，有时也包括了减速运动，这时加速度的方向与速度的方向相反。
v＝v0＋at可以这样理解：由于加速度a在数值上等于单位时间内速度的变化量，所以at就是整个运动过程中速度的变化量；再加上运动开始时物体的速度v0，就得到t时刻物体的速度v。
例题1
汽车以40 km/h的速度匀速行驶，现以0.6m/s2的加速度加速，10s后速度达到多少？
解 初速度v0 ＝40 km/h＝11 m/s，加速度a＝0.6 m/s2，时间t＝10s。
10 s后的速度为
v＝v0＋at＝11 m/s＋0.6 m/s2×10 s＝17 m/s＝61 km/h
描述车辆的速度，通常用的单位是千米每时。
例题2
某汽车在紧急刹车时加速度的大小是6m/s2，如果必须在2s内停下来，汽车的行驶速度最高不能超过多少？
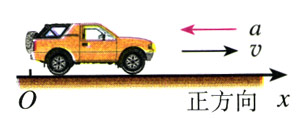
分析 我们研究的是汽车从开始刹车到停止运动这个过程。在这个过程中，汽车做匀减速运动，加速度的大小是6 m/s2。由于是减速运动，加速度的方向与速度方向相反。沿汽车运动的方向建立坐标轴（图2.2-4），则汽车的加速度取负号，记为以a＝－6 m/s2。这个过程的末速度v是0，初速度v0就是我们所求的最高允许速度。过程的持续时间为t＝2 s。
解 根据v ＝v0＋at，我们有
v＝v0－at＝0－（－6 m/s2）×2s＝12 m/s＝43km/h
汽车的速度不能超过43 km/h。
说一说
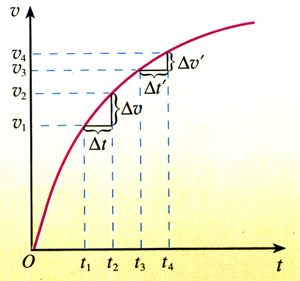
图2.2-5是一个物体运动的v-t图象。它的速度怎样变化？在相等的时间间隔内，即∆tʹ＝∆t时，速度的变化量∆vʹ和∆t总是相等吗？物体在做匀变速运动吗？
问题与练习
1．火车机车原来的速度是36 km/h，在一段下坡路上加速度为0.2 m/s2。机车行驶到下坡末端，速度增加到54 km/h。求机车通过这段下坡路所用的时间。
2．火车在通过桥梁、隧道的时候，要提前减速。一列以72km/h的速度行驶的火车在驶近一座石拱桥时做匀减速运动，减速行驶了2 min，加速度的大小是0.1 m/s2，火车减速后的速度是多大？
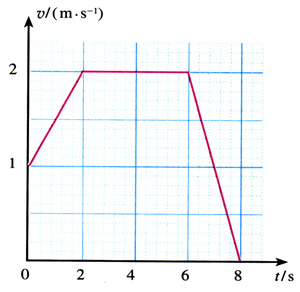
3．一个物体沿着直线运动，其v-t图象如图2.2-7所示。
（1）它在1 s末、4s末、7s末三个时刻的速度，哪个最大？哪个最小？
（2）它在1 s末、4s末、7s末三个时刻的速度方向是否相同？
（3）它在1 s末、4 s末、7s末三个时刻的加速度，哪个最大？哪个最小？
（4）它在1 s末和7s末的加速度方向是否相同？
4．物体由静止开始做加速度为1 m/s2的匀加速直线运动，4 s后加速度大小变为0.5 m/s2，方向仍与原来相同。请作出它在8s内的v-t图象。
发布时间：2015/10/8 下午1:33:58 阅读次数：2362
