第三章 C 牛顿定律的应用

各种交通工具的启动、运行和制动都跟牛顿定律有关。图3-20是一架航天飞机正在安全降落。需要为它提供多长的跑道？这跟它的初速度和加速度有关，其中加速度又跟飞机的受力情况及质量有关。这些都可以运用牛顿定律进行计算。当然这种实际问题的计算比我们现在学习的解题应用要复杂得多。

在日常生活中，牛顿运动定律也有许多简单的实际应用。本节将通过几个实例来讨论它的应用。

大家谈

说说生活实际中，牛顿定律有哪些应用？

一、两类典型问题

应用牛顿定律解决实际问题大致可以归结为哪些最基本的类型呢？

第一类问题：已知作用于物体上的力，由力学规律来求解该物体的运动情况。

第二类问题：已知物体的运动情况，由力学规律来推知作用于物体上的力。

对于第一类问题，由于已知作用力和物体的质量，可应用牛顿定律求出物体的加速度；如果再知道物体运动的初始条件，应用运动学公式就可求出物体的运动情况：任意时刻的位置和速度，以及运动的轨迹等。

对于第二类问题，已知物体运动速度的变化快慢（加速度），可以去推断或者求解物体受到力的情况。

第一类问题是运用已知的力学规律，去探究自然界奥秘和做出科学的预见，这是科学技术活动中进行正确分析和设计的基础之一。发射载人飞船和人造地球卫星到预定的轨道，并能安全降落和回收；在加速器中对粒子加速，都属于第一类课题。它们显示了人们掌握了    通过牛顿第二定律可以求加速度，通过科技知识并能创造性地去运用，可以取得多么辉煌的成就。第二类问题在自然科学发展中的作用也显而易见，根据观察到的物体的运动，通过研究和分析，去认识未知的物体内在相互作用的特点或新的规律。如牛顿万有引力定律的发现，卢瑟福原子的核式结构的发现，都属于这类课题。

点击

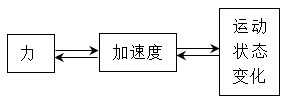
通过牛顿第二定律可以求加速度，通过运动学公式也可以求加速度，因此加速度是联系力和运动状态变化的“中介”。

【示例1】枪膛里的子弹，质量为0.02kg，击发后，假定受到燃烧气体对它的推力恒定为5000N，由静止开始做匀加速直线运动，0.002s后离开枪口，求此时子弹的速度及枪筒的长度。

【解答】本题应属于第一类问题，已知子弹的受力，求解子弹的运动情况。质量为0.02kg的子弹受到燃烧气体的推力F＝5000N后，从初速度v₀＝0的静止状态起做匀加速直线运动，运用牛顿笫二定律可求得子弹的加速度

a＝$\frac{F}{m}$＝$\frac{5000}{0.02}$m/s²＝250000m/s²。

在0.002s后离开枪口时，子弹的速度

v_t＝at＝250000×0.002m/s＝300m/s。

此时子弹走的路程s就是枪筒的长度，

s＝$\frac{1}{2}$at²＝$\frac{1}{2}$×250000×（0.002）²m＝0.5m。

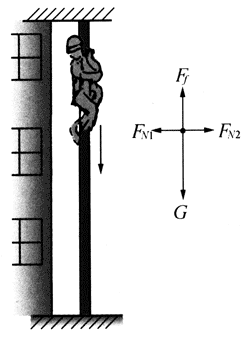
【示例2】如图3-21所示，在某些紧急情况下，消防队员需从高7m的楼上沿金属管从静止起迅速匀加速竖直滑下。为了安全，其着地速度不应大于6m/s，设一消防队员总质量为60kg，他与金属管之间的动摩擦因数为0.4，问他双腿夹紧金属管至少应当用多大的力？（g＝10m/s²）

【分析】设消防队员的重力为G，摩擦力为F_f，压力为F_N1和F_N2（即夹紧的力）它们是一对平衡力，大小相等均为F_N。末速度为v_t，下降高度为h，他可以看作为质点，受力情况如图3-21右边所示。本题属于第二类问题，已知运动状态变化求作用力F_N。

【解答】根据牛顿第二定律

G－F_f＝ma，

其中F_f＝2μF_N，则mg－2μF_N＝ma，可得

F_N＝$\frac{m(g-a)}{2\mu }$。                    ①

由运动学规律可知v_t²＝2ah，即

a＝$\frac{v_t^2}{2h}$。                                   ②

将②式代入①式可得到

F_N＝$\frac{m(g-\frac{v_t^2}{2h})}{2\mu }$，

代入数据后得到

F_N＝$\frac{60\times (10-\frac{6^2}{2\times 7})}{2\times 0.4}$＝$\frac{445.7}{0.8}$N≈557N。

消防队员的腿至少需要用约557N的力夹紧金属管。

【讨论】如果消防队员能用570N的力夹管子，则他着地的速度为多大？

拓展联想

算一算示例2中消防员下滑的时间为多大？

如果他先自由下落，达6m/s速度后匀速下滑，则夹紧的力为多大？下滑总时间为多大？

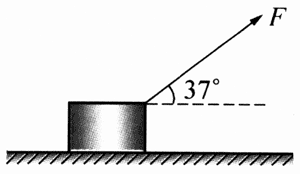
【示例3】工人用绳索拉铸件，从静止开始在水平面上前进。如果铸件的的质量是20kg，铸件与地面间的动摩擦因数是0.25，工人用60N的力拉动铸件，绳跟水平方向的夹角为37°并保持不变（图3-22）。经4s后松手，问松手后铸件还能前进多远？（g＝10m/s²，cos37°＝0.8，sin37°＝0.6）

【分析】由题意可知铸件的运动先后有两个过程，第一个过程是从静止开始运动到松手前，第二个过程是从松手后到停止。

【解答】在第一个过程中，铸件受重力G、拉力F、地面支持力F_N和滑动摩擦力F_f的作用（图3-23）。铸件在这些不变的力的作用下从静止开始做勾加速运动。

把拉力F分解为平行于地面的分力F₁和垂直于地面的分力F₂（图3-24），则

F₁＝Fcos37°，F₂＝Fsin37°。

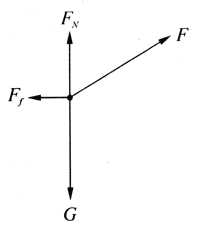
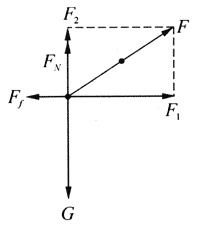
铸件沿水平方向做匀加速直线运动，加速度a方向向前，由牛顿第二定律可得

Fcos37°－F_f＝ma；                           ①

铸件在竖直方向上的合外力为零，即

Fsin37°＋F_N－mg＝0。                     ②

又因为F_f＝μF_N，将②式代入①式，得

Fcos37°－μ（mg－Fsin37°）＝ma

即

a＝$\frac{F\cos {37}^{\circ }-\mu (mg-F\sin {37}^{\circ })}{m}$

＝$\frac{60\times 0.6-0.25\times (20\times 10-60\times 0.6)}{20}$＝0.35m/s²

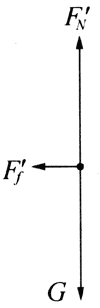
在第二个过程中，松手后绳的拉力为零，铸件受重力G、地面支持力Fʹ_N和滑动摩擦力Fʹ_f的作用（图3-25），此时Fʹ_N＝G。铸件在这些不变的力的作用下做匀减速直线运动，它的初速度v₀即为第一个过程的末速度at，所以

v₀＝at＝0.35×4m/s＝1.4m/s。

铸件做匀减速直线运动的加速度aʹ由滑动摩擦力产生，方向与初速度v₀方向相反，由牛顿第二定律可得

Fʹ_f＝maʹ，

又因为Fʹ_f＝μFʹ_N＝μmg，所以

aʹ＝μg＝0.25×10m/s²＝2.5m/s²。

设铸件前进s后停止，由运动学公式可得

v_t²＝v₀²－2aʹs＝0，

s＝$\frac{v_0^2}{2a^{\prime }}$＝$\frac{{1.4}^2}{2\times 2.5}$m＝0.39m。

即工人松手后，铸件还能前进0.39m。

【讨论】本题虽然仍属于“已知力求运动”问题，但是在过程中力发生了变化，就要根据变化来进行分段求解。可以看出，受力分析和计算加速度是解答本题的关键。

二、连接体问题

如何在多个物体组成的系统中运用牛顿定律？

前面，运用牛顿运动定律解题的研究对象，只是单个物体，我们经常将它看作一个质点。当研究对象比较复杂，由几部分组成，像平板车上载着物体、机车拖着数节车厢这样的问题通常叫做连接体问题。要研究连接体各部分之间相互作用力，或相对运动情况时，可将它的各部分隔离开来进行受力分析，将牛顿定律运用到每一部分上，这时在受力分析和求解问题时就要运用“隔离法”。

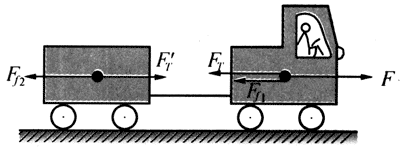
【示例4】一辆汽车拉着一辆拖车在平直道路上行驶，汽车的牵引力是F＝16170N。汽车与拖车的质量分别是m₁＝5000kg和m₂＝2500kg，所受的阻力分别是F_f1＝980N和F_f2＝490N，求它们的加速度和汽车与拖车之间的拉力。

【解答】将汽车和拖车隔离开来，分别研究它们的受力情况。由于它们在竖直方向所受的重力和支持力平衡，可以不予考虑。在水平方向的受力如图3-26所示。汽车受牵引力F，阻力F_f1和拖车对它的拉力F_T作用；拖车受汽车对它的拉力Fʹ_T和阻力F_f2作用。

汽车与拖车一起前进，因此它们有相同的加速度a，根据牛顿第二定律

对于汽车：           F－F_T－F_f1＝m₁a；                    ①

对于拖车：           Fʹ_T－F_f2＝m₂a。

由牛顿第三定律知道，F_T和Fʹ_T是一对作用力和反作用力，大小相等，则对于拖车可改写成

F_T－F_f2＝m₂a              ②

将①式和②式相加可以得到

F－F_f1－F_f2＝（m₁＋m₂）a，

所以              a＝$\frac{F-F_{f1}-F_{f2}}{m_1+m_2}$＝$\frac{16170-980-490}{5000+2500}$m/s²＝1.96m/s²。

将a代入②式，得

F_T＝F_f2＋m₂a＝（490＋2500×1.96）N＝5390N。

所以汽车和拖车的加速度是1.96m/s²，它们之间的拉力是5390N。

自主活动

在求加速度时能不能将汽车和拖车看成一个整体，用牛顿第二定律求解？

【讨论】解答本问题时，也可以先将汽车和拖车看成一个整体。求出这个整体所受合外力，即F－F_f1－F_f2，求出加速度，再用隔离法求拉力。

大家谈

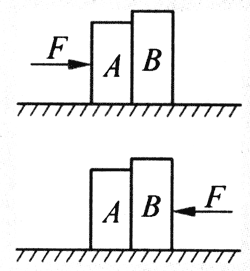
如下图3-27所示，质量不同的两木块紧挨着放置在光滑水平桌面上，今用水平恒力F推木块，当F向左时与F向右时，两木块间相互作用力相同吗？

点击

从连接体问题可知，牛顿第二定律不仅适用于整个物体，同样也适用于物体的局部。

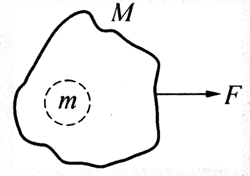
如图3-28中一物体质量为M，受外力F作用做加速运动，这时物体中有质量为m的局部，它受到物体其余部分对它的作用力为

Fʹ＝ma＝m$\frac{F}{M}$。

三、估算方法

估算是一种非常有用的方法，它不需要通过严密的计算，便可得出比较可靠的结论，它在物理学研究中用得很广。

【示例5】鸵鸟是当今世界上最大的鸟。有人说它是因翅膀退化了才不会飞。如果鸵鸟长了一副与它身体相匹配的翅膀，它就能飞起来吗？已知鸟在飞行中受到的上举力F_举＝CSv²（式中S为翅膀的面积，v为鸟飞行的速度，C为一比例常数）。

【解答】在这个问题中我们采用如下的估算方法。鸟飞翔的必要条件是上举力F_举至少与体重G平衡，在公式F_举＝CSv²中，S是鸵鸟翅膀的面积，它是不变的，所以F_举仅是鸟飞行速度v的函数。鸟能起飞的条件是F_举大于G，即

CSv²＞mg，

v＞$\sqrt{\frac{mg}{CS}}$。

现取v的最小值，即鸟起飞的临界速度v_C＞$\sqrt{\frac{mg}{CS}}$，作一简单估算。设鸟的几何线度为L（即将鸟看作是边长为L的立方形物体），其体积为L³，它的质量m正比于L³，S正比于L²，即鸟起飞的临界速度v_C正比于$\sqrt{\frac{gL}{C}}$，即正比于$\sqrt{L}$，查资料知道燕子的最小滑翔速度约为20km/h。而鸵鸟的体长L约为燕子的25倍，从而它跑动起飞的临界速度应是燕子的$\sqrt{25}$＝5倍，即100km/h，这已达飞机起飞的速度数量级，尽管鸵鸟擅长奔跑（40km/h），也就勉为其难了。所以即使鸵鸟有了一双与它身体大小成比例的翅膀，也不可能飞起来。

从解这个问题的过程可以看出，除了正确运用物理定律外，如能采用正确的估算方法，并查阅一些相关资料，有些看似难解的问题就可迎刃而解了。这也是物理学家探索科学奥秘中常用的有效方法之一。

发布时间：2015/10/1 下午10:08:40  阅读次数：2342