第5节 速度变化快慢的描述——加速度 教学参考

1．教学目标

（1）理解加速度是描述物体速度变化快慢的物理量，了解加速度的定义式和单位。

（2）了解如速度的矢量性，会根据速度与加速度方向的关系判断运动性质。

（3）通过加速度概念的建立过程和加速度定义式的得出过程，了解和体会比值定义法在科学研究中的应用。

（4）理解加速度的概念，区别速度、速度变化量和速度变化率，能在生活中准确地使用加速度的概念。

（5）能用v-t图象计算加速度的大小，体会数学在物理中的重要性。

2．教材分析与教学建议

加速度是力学中的重要概念，也是高一年级物理课程中比较难懂的概念之一。在学生的生活经验中，与加速度有关的现象不多，这就给学生理解加速度概念带来困难。为此，教科书先列举小型轿车和旅客列车起步后的加速过程，让学生思考它们速度变化的快慢，以增强学生的感性认识，之后教科书还展示飞机的起飞过程。在具体的事例中，要求学生了解“速度大”、“速度变化大”和“速度变化快”含义的不同。同时，通过旁批提醒学生注意“物体运动的快慢”与“运动速度变化的快慢”的不同。

用v-t图象描述运动速度变化，可以直观和形象地认识速度的变化规律。比如图线是直线，说明速度变化是均匀的，即加速度是恒定的。这对理解平均加速度与瞬时加速度的关系也是很有利的。学生通过教科书设置的“思考与讨论”和“科学漫步”栏目的内容，在图象中认识变化率，可以加深对加速度的认识，并进一步对图象加以理解。

常有人说“不要把物理教学数学化”，好像数学茌物理教学中会起到消极作用。实际情况恰恰相反，物理学的发展离不开数学，学好高中物理也离不开数学。本书力图加强数学在物理教学中的作用，图象的充分利用就是一个重要方面。

（1）加速度

学生对加速度认识的快慢，与如何引入加速度概念有着密切的关系。因为在学生的生活验中没有与加速度相关的知识，所以，教学中应该首先利用实例让学生感受到对速度变化快慢的描述是有意义的。如教科书中比较小型轿车和旅客列车加速的情况，通过比较并组织学生思考、讨论，使学生对以下几个问题有很深的印象：

①“速度大”、“速度变化大”和“速度变化得快”所描述的运动是不一样的。

②做变速运动的物体，有的速度变化快，有的速度变化慢。

③研究物体速度变化的快慢是有意义的。

④需要引入一个物理量来描述速度变化的快慢。

引入加速度的思路是老师们比较熟悉的，但是要注意落实本节开始时的“思考与讨论”。教学时让学生充分发表意见，才会使学生们感到有必要引入一个新的物理量来描述速度变化快慢的问题。

教学中也可以考虑制作课件演示汽车的加速过程和制动过程中速度变化的情况，如图1-2所示。

让学生注意观察汽车速度的变化，思考研究速度变化的意义。教师可组织学生讨论，并明确下列问题：

• 汽车的加速性能是反映汽车质量优劣的一项重要指标；
• 汽车的制动距离也是反映汽车性能的一项指标；
• 研究速度变化快慢是有意义的；
• 需要引入一个物理量来描述速度变化的快慢。

速度变化率反映的是速度变化的快慢，它就是加速度。所以理解加速度a的过程，就是要逐渐地去理解速度v、速度变化Δv和速度变化率\(\frac{{\Delta v}}{{\Delta t}}\)之间的关系和区别。为此，可考虑设计以下问题启发学生思考：

• 有可能出现速度大，加速度小的情况吗？
• 有可能出现速度变化量小，而加速度大的情况吗？
• 有可能出现速度方向与加速度方向相反的情况吗？
• 有可能出现加速度方向与速度变化量方向相反的情况吗？
• 有可能出现加速度增大，而速度减小的情况吗？

讨论这些问题时，可以利用加速度定义式进行讨论，然后结合实例让学生理解。

（2）加速度方向与速度方向的关系

对加速度方向的认识取决于对速度变化量Δv的认识，而速度变化量对初学矢量的学生是不容易理解的。因为学生很难将速度和速度变化区别开，特别是速度的方向和速度变化的方向可能相同，也可能不相同。教学时，可以先让学生回忆第3节研究位置变化的过程，用Δx＝x₂－x₁计算位移时，位移的方向可能与坐标的正方向相同，也可能与坐标的正方同相反。但是位移Δx的方向与速度方向一定相同。

通过回忆，学生可以很好地理解速度变化实际上是在进行矢量减法。当初、末速度在同一直线上并确定速度的方向后，速度变化量Δv＝v₂－v₁可能与速度方向相同，也可能与两个速度的方向相反。如，已知v₁＝10m/s，v₂＝30m/s，则Δv＝v₂－v₁＝20m/s，这时速度变化量的方向与速度方向相同。若已知v₁＝30m/s，v₂＝10m/s，则Δv＝v₂－v₁＝－20m/s，这时速度变化量的方向与速度方向相反。结合实际情况我们看到，物体加速时Δv的方向与速度v的方向相同。物体减速时Δv的方向与速度v的方向相反。

另外，在处理矢量减法时也可以将Δv＝v₂－v₁处理为v₂＝v₁＋Δv，如已知v₁＝30m/s，Δv＝－20m/s则Δv＝v₂－v₁＝30m/s＋（－20）m/s＝10m/s。对图中的有向线段可以这样引导学生去理解：将速度v₁与方向相同的Δv相加，正好是两个有向线段头尾相连，得到的就是v₂，如图1-3甲。将速度v₁与方向相反的Δv相加，两个有向线段头尾相连，得到的如图1-3乙中的v₂。

用正负号表示矢量方向，将同一条直线上的矢量加减法变为标量的代数加减法，这些新鲜内容对学生来说能够提高思维能力，但是同时也带来了困难。教学中要帮助学生在掌握方法的过程中树立自信心，磨炼学生征服困难的意志品质。

学生理解平均加速度的定义是不难的。虽然课本并没有给瞬时加速度明确下定义，但是在说明什么是匀变速运动时，用了“加速度不变的运动”。仔细体会这句话，可以知道这里的加速度就是指瞬时加速度。如何找出平均加速度与瞬时加速度之间韵关系，教师可以将学习加速度的过程与学习速度的过程加以比较。在比较中，学生可能很容易理解平均加速度与瞬时加度之间的关系。比如，教师在引导学生做以下比较时很容易得到以下结果——速度是位置的变化率，加速度是速度的变化率；速度与位移的方向相同，加速度与速度变化量的方向相同；在Δt很小时，平均速度接近瞬时速度，那么在Δt很小时，平均加速度就应该接近瞬时加速度。

教学中也可以再一次应用极限的思想将平均加速度过渡到瞬时加速度。当学习了v-t图后，还可以用图象中直线或曲线的斜率来理解平均值和瞬时值的关系。教师用什么方法解决这一难题，要根据学生的情况加以选择，不要操之过急。在第二章的学习中还有机会不断地理解，如利用课本第39页“说一说”栏目的内容就可以进一步理解。

（3）从v-t图象看加速度

课本第28页“思考与讨论”的问题，是要求学生从速度-时间图象中看出物体的加速度。本书没有涉及“斜率”这个术语，但是学生应该知道曲线的倾斜程度反映加速度的大小。学生要能从图象上量出Δv和Δt的值，然后根据定义计算加速度。

教学中要注意引导学生通过v-t图象了解速度与速度变化率的关系。在v-t图中理解加速度是教学的重点。教师可以启发学生回答以下问题：在v-t图象中是怎样表示速度变化多少的？怎样反映速庋变化快慢的？

用v-t图研究物体运动的方法不仅重要，而且也不仅限于速度和速度变化率。但本节教学的重点只放在速度和速度变化率上，不要讲得太多。

3．问题与练习

内容分析

本节练习有4题，练习的内容都是非常重要的。第1题联系实际计算三种车型的平均加速度，可以使学生加强对加速度是描述汽车性能的重要参数的认识，增加学生对加速度应用的认识。第2题通过选择题的形式，使学生进一步地辨析速度与加速度的不同，以及两者之间的关系。第3题从图象的角度再次比较速度与加速度。对第一次接触加速度概念和v-t图象的学生，这些内容是有难度的，教师要有耐心并要讲究方法。第4题涉及气垫导轨和数字计时器及光电门。除了练习计算加速度外，还有助于加深理解平均速度与瞬时速度的关系。分别算出两个遮光板经过光电门时的平均速度，这就是过程始末的瞬时速度。有人还要推算两个遮光板的前沿经过光电门的瞬时速度，其实没有这种必要。究其思想深处，还是“追求无限精确”的思想在作怪，这种思想脱离实际，应该改变。

解答与说明

1．解答：

由v＝100km/h＝27.8m/s

可知a_A＝\(\frac{{v - 0}}{{\Delta {t_1}}}\)＝\(\frac{{27.8}}{{11.3}}\)m/s²＝2.45m/s²

a_B＝\(\frac{{v - 0}}{{\Delta {t_2}}}\)＝\(\frac{{27.8}}{{13.2}}\)m/s²＝2.11m/s²

a_C＝\(\frac{{v - 0}}{{\Delta {t_3}}}\)＝\(\frac{{27.8}}{{15.5}}\)m/s²＝1.79m/s²

2．解答：A．汽车做匀速直线运动时加速度等于0，速度不等于0。

B．火车从静止加速到100km/h需要50s。轿车从静止加速到100km/h需要15s。

C．物体向西做减速运动时，速度方向向西，但加速度向东。

D．汽车加速到最大速度的过程中，汽车会做加速度减小的加速运动，速度增大，加速度减小。

3．解答：A的斜率最大，加速度最大。

a_A＝0.63m/s²，a_B＝0.083m/s²，ac＝－0.25m/s²，A、B的加速度方向与速度方向相同，C的加速度方向与速度方向相反。

4．解答：

滑块通过第一个光电门的速度v₁＝\(\frac{{3.0}}{{0.29}}\)cm/s＝10cm/s

滑块通过第二个光电门的速度v₂＝\(\frac{{3.0}}{{0.11}}\)cm/s＝27cm/s

滑块的加速度a＝\(\frac{{\Delta v}}{{\Delta t}}\)＝ \(\frac{{27-10}}{{3.57}}\)cm/s²＝4.8cm/s²

教学设计案例

【教学过程】

教学目标

（1）知道加速度是描述物体速度变化快慢的物理量，了解加速度的定义式和单位。理解加速度概念，区别速度、速度变化量和速度变化率。

（2）了解加速度的矢量性，会根据速度与加速度方向的关系判断运动性质。

（3）通过加速度概念的建立过程和加速度定义式的得出过程，了解和体会比值定义法在科学研究中的应用。

（4）会利用加速度定义式计算匀变速直线运动的加速度。

（5）会利用v-t图象计算加速度的大小。

导入新课

教师：对运动的描述，首先从描述物体位置变化入手。关于位置变化、位置变化的快慢，物理学是通过哪些物理量描述的？

学生作答，引出位移和速度概念。希望学生能注意到研究问题的思路，达也是本节研究速度变化的思路。

教师：用速度可以描述物体位置改变的快慢，即运动的快慢。而速度变化时，如何描述速度变化的快慢呢？以下是一些物体速度变化时的数据。通过数据，你能感受到什么？

学生发表看法。讨论目标是：物体速度变化可以与时间相比较，也可以与位移相比较。

进行新课

1．探究用什么物理量表示速度变化快慢

师：通过以上数据我们看到，描述物体速度改变时，可以通过时间来比较，也可以通过位移来比较。如果用Δv表示速度的变化，Δt表示时间，Δx表示位移，你认为应该用\(\frac{{\Delta v}}{{\Delta t}}\)表示速度的变化快慢，还是应该用\(\frac{{\Delta v}}{{\Delta x}}\)表示速度变化快慢更好？

请同学们不急于回答问题，先阅读课文，然后再提出自己的看法。

学生阅读课文。教师准备实验。

师：同学们在阅读课文后可能已经有了自己的答案。在请同学们表达自己意见之前，老师还有一个建议。希望你们在阐述自己观点时，能用数据说话。现在我用这套实验装置做实验，打出纸带发给大家。你们要通过纸带提供的数据，用计算的数值来为你的见解提供证据。

做实验，打出的若干条纸带，交给不同小组的同学。要求学生在纸带上找出几个计数点（相邻两个计数点间的时间间隔取0.1s）。计算几个计数点的速度，然后研究速度变化与时间、位移的关系。

因为学生才做过一次分组实验，如何计算纸带上计数点的速度，最好能提示学生。在这里，学生只能用平均速度来表示瞬时速度。

等学生做好准备后，请学生利用手中的数据回答并阐述到底是用描述速度变化快慢，还是用描述速度变化快慢的观点。

教学目标：通过纸带分析速度变化与时间和位移关系时，只要学生能认识到速度变化与时间的关系比较容易寻找就可以了。比如，在这次实验中物体做匀变速直线运动（虽然学生并不知道其中的规律），因此学生很难看出\(\frac{{{v_1} - {v_0}}}{{\Delta {x_1}}}\)、\(\frac{{{v_2} - {v_1}}}{{\Delta {x_2}}}\)、\(\frac{{{v_3} - {v_2}}}{{\Delta {x_3}}}\)之间的关系，却很容易看出\(\frac{{{v_1} - {v_0}}}{T}\)＝\(\frac{{{v_2} - {v_1}}}{T}\)＝\(\frac{{{v_3} - {v_2}}}{T}\)。学生能够发现这些关系，教学的目的也就达到了。

学生通过实验数据说明，用\(\frac{{\Delta v}}{{\Delta t}}\)描述速度变化快慢比用\(\frac{{\Delta v}}{{\Delta x}}\)描述速度变化快慢更简单。如果学生用生活经验（生活中比较快慢总是与时间有关），或用第3章学习速度的方法来说明应该用\(\frac{{\Delta v}}{{\Delta t}}\)描述速度变化快慢也是可以的。

2．关于加速度定义的学习

学生阅读过课文，再经过以上的探究活动，可以直接引出加速度的定义式。

师：既然速度变化的快慢用\(\frac{{\Delta v}}{{\Delta t}}\)表示更简单，物理学中就用它来表示速度变化的快慢，取名为加速度，即a＝\(\frac{{\Delta v}}{{\Delta t}}\)。

师：在研究位置变化快慢时，根据速度定义式我们可以了解速度的单位，可以知道速度的方向。现在，根据加速度定义式，你能知道加速度的单位吗？加速度是矢量还是标量？加速度的方向与哪个物理量的方向有关？

用比较的方法引导学生用定义式研究物理量的方法。学习目标：使学生通过加速度的定义式知道加速度的单位是m/s²；知道加速度是矢量，其方向与速度变化的方向相同。知道根据加速度定义式得到的值是平均加速度，平均加速度在匀变速直线运动中等于瞬时值。

（第1课时结束）

3．在v-t图（图1-4）中认识速度v和加速度a＝\(\frac{{\Delta v}}{{\Delta t}}\)。

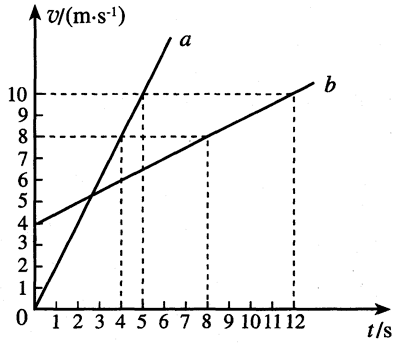
师：这是v-t坐标系，图中直线a和直线b分别表示两个物体运动时速度随时间变化的图象。根据图中数据，请尽可能多地描述两个物体运动的情况。

教学过程中教师可以启发学生思考：图象所描述的物体，运动轨迹是直线吗，为什么？任意时刻的速度都大于零说明什么？直线的斜率大于零说明什么？v-t坐标系中轨迹是直线，是否表示物体做匀变速直线运动？

教学目标：

通过对速度大小和方向的描绘初步认识v-t图象；

学习对运动轨迹的描绘；

通过对速度变化的描述，使学生在对物体运动状态认识的过程中熟悉图象。

在此基础上，继续给学生提供不同v-t图象进行练习，如描述图1-5中甲、乙两图表示的运动。通过练习，使学生在图象中认识速度、速度变化和加速度的能力不断加强。

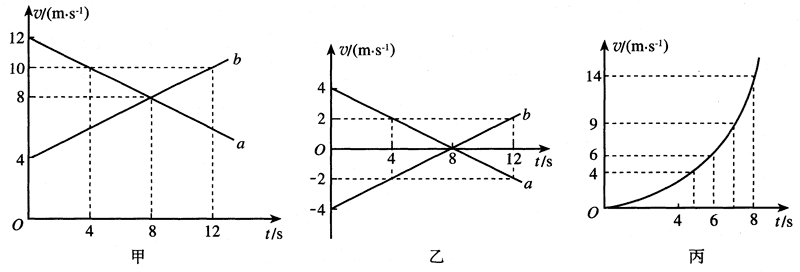
4．关于平均加速度和瞬时加速度的教学

师：在v-t图中，图线是直线时反映物体做匀变速直线运动，直线的斜率反映物体的加速度。如果图线是曲线，如图1-5中的丙图，它反映的是什么运动？为什么？

安排这些讨论的目标是：只要学生能说到物体做加速度增大的加速运动就可以了

【教学设计说明】

本节是第一章的最后一节内容。当结束本节学习时，描述运动的物理量如位移、速度和加速度学生就都学过了一遍。虽然课本呈现内容的思路非常清晰，但是学生对这些内容的学习仍会有困难。困难主要有两点，一是初学矢量，再是不能很好地理解变化率。如何突破这些难点，就成了教学的重点。

在第3节学习中，学生已经经历过一次“位置的变化→位置变化的多少→位置变化的快慢”，“位置变化的方向就是速度方向”和“平均速度与瞬时速度”的学习。这为本节学习速度、速度变化和加速度之间关系，了解加速度定义式的意义有着很好的帮助。知道加速度与速度变化、与时间和位移有联系，为下一章匀变速直线运动的学习提供了可靠的保障。

学生接受加速度概念的困难之一是因为生活中缺少相关的经验。因此，让学生在生活的事例中找到加速度的应用，能够自己寻找到描述速度变化快慢的方法，就会降低学习的难度。所以在这节课中增加了一个，“探究描述速度变化快慢的物理量”的内容。期望学生通过生活中的事例认识到研究速度变化的实用意义；认识到速度变化的过程不仅与时间有关也与位移有关，但是为什么最后人们是用\(\frac{{\Delta v}}{{\Delta t}}\)来描述速度变化的快慢。

安排实验的目的是，通过数据处理说明究竟用\(\frac{{\Delta v}}{{\Delta t}}\)还是用\(\frac{{\Delta v}}{{\Delta x}}\)描述速度改变快慢更好。所以课中安排的实验只是用来获取实验数据让学生进行分析。因此，本节课可以不安排学生做分组实验，实验也可做演示实验。

用加速度的定义式进一步学习与加速度相关的问题，比如对单位，矢量性，方向的判断，平均、瞬时性的了解，是学生需要学会的一种方法。所以在新课教学中安排了“关于加速度定义的学习”的内容，教学中可以比较学习速度概念时的方法和过程。

用图象方法研究物理问题是高中教学的一个重要任务，虽然在第4节学生已经知道，用v-t图可以描述速度变化的规律，但是怎样用v-t图来研究运动规律，本节是第二次。而在第二章学习中将会大量使用这种方法研究运动的规律，所以在本节教学时重点应放在如何在v-t图中找出速度、速度变化和速度变化率（加速度），并能概括出它们之间的关系。

本节课的内容比较多而且有一定的难度，再加上多了一个探究活动，课时安排应为2课时。第1课时可以在“从v-t图象看加速度”前告一段落。第2课时的重点放在图象法上。

发布时间：2015/9/29 下午9:12:21  阅读次数：507