B 有固定转动轴物体的平衡

图2-9是位于哈尔滨太阳岛风景区的“太阳桥”，它是一座全钢结构独塔无背索斜拉桥，设计独特。这座外形简洁的斜拉桥全长460m，宽15.5m，主塔高93.5m，向后倾斜，犹如风帆远行。每当夜晚，各色灯光将大桥照耀得绚丽多彩，轮廓分明。图2-10则是德国慕尼黑的奥林匹克公园，1972年在那里举行了第20届奥运会，该场地的看台屋顶建筑在当时具有非常独特而超前的风格。

在诸如桥梁和建筑物的设计中，它们的平衡问题是一个首要问题。为简单起见，这里我们仅讨论有固定转动轴的物体的平衡问题。当有固定转动轴的物体处于静止状态或匀速转动状态时，我们就说它处于转动平衡状态。

那么，当有力作用在有固定转动轴的物体上时，在怎样的条件下它才能保持平衡呢？

大家谈

如图2-11，杆可绕通过其中点垂直于纸面方向的固定轴O转动。如果在杆的左侧施加一个垂直于杆的力F，要求杆保持平衡状态，应怎样施加另外的一个或几个力。

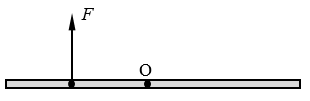
通过上节的学习和对“大家谈”栏目中问题的讨论，你可能会意识到，因为力对物体转动状态改变的作用效果与“力矩”这个物理量有关，所以上述问题又可进一步明确为：作用在一个有固定转动轴物体上的所确力矩应满足怎样的条件，才能使该物体处于平衡状态？

探索研究

【学生实验】

研究有固定转动轴的物体的平衡条件

【实验目的】研究有固定转动轴的物体的平衡条件。

【实验器材】铁架台、力矩盘、弹簧秤、一组钩码、带套环的横杆、钉子、细线、三角板等。

【探究思路】

作用在有固定转动轴物体上的力矩可引起物体沿不同方向转动。从沿着转动轴的某一个方向上看，力矩的作用效果不外乎有两种可能：引起物体沿逆时针方向转动或者沿顺时针方向转动。于是我们要通过实验来探究的问题是，为了使一个有固定转动轴的物体处于平衡状态，施加在该物体上的能引起它沿逆时针方向转动的力矩和能引起它沿顺时针方向转动的力矩之间究竟需满足怎样的定量关系。

【实验步骤】

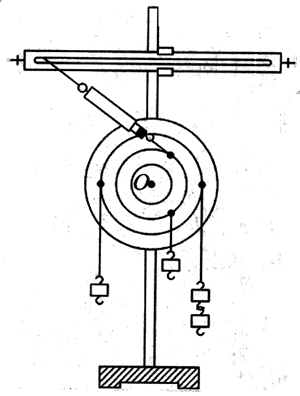
（1）如图2-12所示，将力矩盘的金属轴O固定在铁架台上，把力矩盘套在轴上并使盘面保持竖直。同时在铁架台上固定一根横杆。力矩盘上画出的同心圆供确定力臂时参考。

（2）将钉子固定在力矩盘的四个任意位置上，其中三枚钉子上用细线悬挂不同个数的钩码，第四个钉子用细线与测力计的钩子相连，测力计的另一端则挂在水平横杆的套环上。

（3）当力矩盘在这四个力的作用下处于平衡状态时，测出各个由大小及它们的力臂。将力和力臂的数据记录在预先设计的表格中。

（4）改变钉子的位置，重复实验一次。

（5）分析数据，得出结论。

计算各个力对转轴O的力矩；确认该力矩究竟是逆时针方向力还是顺时针方向力矩，然后分别算出能引起物体沿逆时针方向转动和沿顺时针方向转动的力矩之和，并由此得出关于有固定转动轴物体的平衡条件。

通过实验我们可以得到如下结论：作用在一个有固定转动轴物体上的能引起它沿逆时针方向转动的力矩之和与能引起它沿顺时针方向转动的力矩之和相等时，该物体便处于“转动平衡”状态，这个结论称为“力矩平衡条件”，该条件可用公式表示为

M_逆＝M_顺，

其中M_逆、M_顺分别表示能引起物体沿逆时针方向和顺时针方向转动的力矩之和，初中物理课程中介绍的杠杆平衡条件（有时也称为杠杆原理）是上述力矩平衡条件的简单特例。

拓展联想

一般物体平衡条件包括“力平衡条件”和“力矩平衡条件”。

在实际的建筑和桥粱设计中，对于其中每个部件都要进行受力分析，建立起关于力的平衡条件和力矩平衡条件的方程，这些方程互相联系，构成一个包含大量方程的联立方程组。对于这样的方程组，需要利用计算机进行计算和分析，从而选择出最佳设计方案。

示例1 如图2-13所示，商店的招牌可以做得非常漂亮。

现在来考察一个物理问题，如图2-14所示，一块质量M为6kg的招牌悬挂在一根质量m为1kg、长度L为2m的均质横杆OA上的A端处，横杆可绕通过O点且垂直于纸面的固定轴自由转动。一根细铜丝CD拉住这根横杆，使它保持在水平位置，OD的长度l为1.5m，细钢丝与横杆的夹角θ为30°。求钢丝对横杆的拉力F_T。

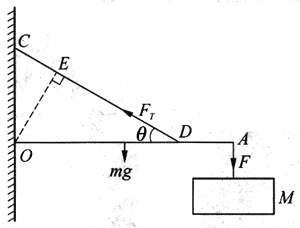
分析 我们考察的有固定转动轴的物体是横杆OA。现在需要找出作用在横杆OA上的力，并确定它们对转轴的力矩。这些力是招牌对横杆A端的拉力F＝Mg、横杆的重力mg、钢丝CD中的拉力F_T。其中F和mg的力矩能引起横杆沿顺时针方向转动；F_T的力矩能引起横杆沿逆时针方向转动。利用力矩平衡条件可得到这些力对O轴的力矩的一个关系式，从而算出F_T。

解答 F的力臂L=2m；mg的力臂$\frac{L}{2}$＝1m；钢丝拉力的力臂lsinθ。由力矩平衡条件可得

MgL＋mg$\frac{L}{2}$＝F_Tlsinθ

由此解出F_T：

F_T＝$\frac{(ML+\frac{ml}{2})g}{l\sin \theta }$

＝$\frac{(6\times 2+1\times 1)\times 9.8}{1.5\times \sin {30}^{\circ }}$N

＝170N

讨论 也可用正交分解法计算F_T对于转动轴O的力矩。F_T垂直于横杆OA的分力为F_Tsinθ，它对转动轴O的力矩为F_Tsinθ·l。而F_T平行于横杆OA的分力为F_Tcosθ，它对O轴的力臂为零，因此它对O轴的力矩为零。

大家谈

在示例1的分析中，我们考察了作用在横杆OA上三个力所产生的力矩是否还有别的力作用在这根横杆上？为什么不考虑？

点击

用力矩平衡条件求解有固定转动轴物体平衡问题的一般步骤：

1．确定考察对象及转动轴；

2．作受力分析（对通过O点的力可不考虑）；

3．找出M_逆和M_顺；

4．列出力矩平衡条件方程，解出未知量。

示例2    图2-15（a）是上海市外环线沉管隧道施工时的现场，图2-15（b）是一台河边码头用的起重机示意图。设起重机吊杆长l＝7.5m，重W＝2.5kN，其重心离底端O点距离l₀＝3m处。通过拉索可改变吊杆仰角θ。设θ＝45°，拉索的额定拉力F＝20kN。问：当拉索与吊杆的夹角α＝30°时，这台起重机能吊起货物的最大重力G是多少？

解答 重物对吊杆作用力的力臂为lcosθ；吊杆重力对O点的力臂为l₀cosθ；拉索拉力的力臂为lsinα。利用力矩平衡条件可得

Glcosθ＋Wl₀cosθ＝Flsinα

由此解出G：

G＝$\frac{Fl\sin \alpha -W{l}_0\cos \theta }{l\cos \theta }$

＝$\frac{20\times 7.5\times \sin {30}^{\circ }-2.5\times 3\times \cos {45}^{\circ }}{7.5\times \cos {45}^{\circ }}$×10³N＝1.3×10⁴N

示例3 汽车的发动机能产生多大转动力矩，是一辆汽车的重要性能指标之一。

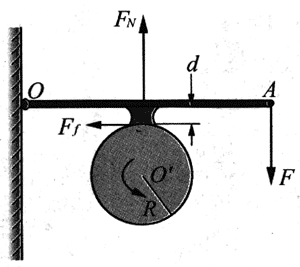
为了测量发动机在特定转速下所产生的力矩，可采用如图2-16所示的“测力（矩）计”装置。长度为L的横杆OA可绕通过O点且垂直干纸面的轴自由转动。在A点施一竖直向下的力F，使横杆中点处的摩擦块紧紧压住安装在发动机上的正在转动的飞轮边缘，调节力F的大小，使飞轮达到某一确定的转速。此时保持横杆水平，设横杆长L＝1.2m；摩擦块厚d＝6cm；飞轮的半径R＝20cm；F＝625N；飞轮对摩擦块的压力F_N＝1290N，忽略横杆的质量。求发动机在此转速时所产生的力矩。

分析 除通过O点的力外，横杆上受到三个力：F、飞轮的压力F_N和摩擦力F_f。它们对O点的力臂分别为L、$\frac{L}{2}$、d。它们对O点的力矩中，F和F_f的力矩是顺时针方向力矩；而F_N的力矩是逆时针方向力矩。

解答 应用关于横杆OA的力矩平衡条件，有

LF＋d·F_f＝$\frac{L}{2}$·F_N

发动机飞轮为了克服摩擦力（其方向与图中F_f的方向相反，大小相等），维持以恒定的速度转动，需提供的力矩的大小为M＝RF_f，于是可得

M＝$\frac{(\frac{1}{2}{F}_N-F)LR}{d}$

代入数据，

M＝$\frac{(\frac{1}{2}\times 1290-625)\times 1.2\times 0.2}{0.06}$N·m＝80N·m

讨论 实际上，利用滑动摩擦力与正压力的关系（F_f＝μF_N，其中μ为动摩擦因数，参见后面第四章)，不必测量正压力F_N，已知动摩擦因数μ与力F，就可得到M。

STS

我国生产的某种型号轿车技术参数中的一项重要指标是：“最大转矩/转速（N·m/rpm）126/3800”，即在每分钟3800转时，产生的最大力矩为126N·m。

发布时间：2015/9/27 下午9:03:04  阅读次数：1935