八、共点力作用下物体的平衡

物体处于静止或者做匀速直线运动的状态叫做平衡状态。要使物体在力的作用下处于平衡状态，作用在物体上的力就必须满足一定的条件，这个条件叫做平衡条件。

懂得物体的平衡条件；对生活和生产都是非常必要的。从一张课桌椅的安放，到一枚火箭在发射台上的安置，都离不开使它们达到平衡的要求。杂技演员和体操运动员在走钢丝和表演技巧运动（本章导图3）时，首要的一点就是必须保持他们自身的平衡。

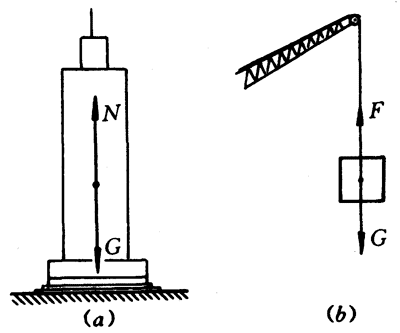
我们在初中已经学习过二力平衡条件，就是当物体受到两个共点力作用时，只有这两个力沿同一直线、大小相等、方向相反，物体才能保持平衡。矗立在地面上的建筑物，同时受到重力G和地面弹力N的作用[图4-54（a）]。被起重机钢索吊住的集装箱，同时受到重力G和拉力F的作用[图4-54（b）]。这些物体都处于平衡状态，所以它们所受的这两个力必然是大小相等，方向相反，并在同一直线上的。如果从力的合成角度来看，很明显，这两个力的合力等于零，这就是在两个共点力作用下物体的平衡条件。

现在，我们再进一步研究，在三个共点力作用下物体的平衡条件。

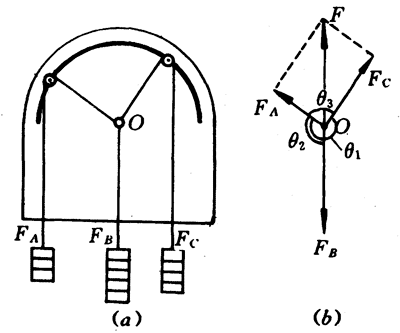
将研究力的合成时所用的装有滑轮的竖直板倒过来放置（图4-55），用三根细绳系住一个轻质小圆环O，将其中两根细绳跨过定滑轮，然后在三根细绳的另一端分别挂上适当数量的钩码，并调节两个滑轮的位置，使圆环O受到三个力的作用而保持平衡状态[图4-55（a）]。根据所挂钩码的数量，记下三根细绳作用在圆环O上的拉力F_A、F_B和F_C的大小，并量出三根细绳间的夹角θ₁、θ₂和θ₂，作出F_A、F_B和F_C的图示[图4-55（易）]，求出F_A和F_C的合力F。可以看出，F和F_B是在同一直线上、大小相等、方向相反的两个力，所以它们的合力等于零，也就是F_A、F_B和F_C这三个共点力的合力等于零。可见，三个共点力作用下物体的平衡条件是这三个力的合力等于零。

实验同样可以证明，在三个以上共点力作用下物体的平衡条件也是这些力的合力等于零。这样，我们就可以得出结论：在共点力作用下物体的平衡条件是合力等于零。

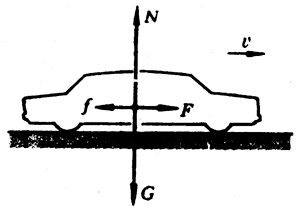
做匀速直线运动的物体也是处于平衡状态的。所以在共点力作用下，做匀速直线运动的物体，所受共点力的合力也应该等于零。例如起重机钢索吊住的集装箱，被匀速竖直向上提起，在不考虑空气阻力的条件下，钢索拉力F和重力G的合力等于零；如果考虑空气阻力，拉力、重力和阻力这三个力的合力也等于零。再如沿平直公路匀速行驶的汽车；受到发动机牵引力F、摩擦阻力f、重力G和路面弹力N的共同作用（图4-56），这四个力的合力一定也等于零。在竖直方向上，重力和弹力大小相等，方向相反；在水平方向上，牵引力和阻力大小相等，方向相反，即G＝N；F＝f。

掌握共点力的平衡条件，在工程技术中有着极为重要的意义。原先平衡的物体，如果受力情况有变化，平衡条件就会受到干扰，物体的平衡就可能遭到破坏，从而造成事故。

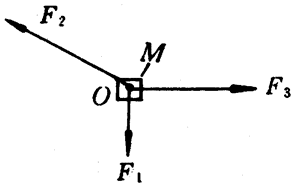
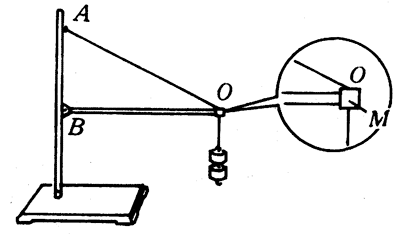
我们可以利用铁架台制作一个简单的支架模型进行观察。如图4-57所示，OA是一段绳索，OB是一根水平放置的木杆，它的B端顶在铁架台的直杆上，另一端有一块轻质小方木M。小方木的上、下分别与绳索和挂钩码的悬绳相连接。当在悬绳下挂上钩码时，小方木M就紧压在木杆上。现在把小方木作为研究对象，可以看出，它受三个共点力作用而保持平衡（小方木自身所受重力可忽略不计）：一是悬挂钩码的悬绳的向下拉力F₁；二是绳索沿OA方向的拉力F₂；三是木杆对它的支撑力（弹力）F₃，方向沿着木杆，由B指向O，它们的合力为零（图4-58）。这时，如果将木杆取走（撤去力F₃），或将绳索剪断（取消力F₂），小方木就都不能再在原来位置保持平衡。

【例题1】

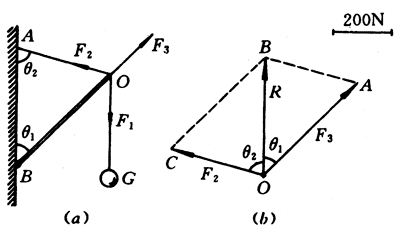
受到400牛重力的钢球悬挂在由轻质撑杆和绳索组成的支架上，如图4-59（a）所示。已知θ₁＝45°，θ₂＝75°，试用作图法求撑杆和绳索的支撑力和拉力。

解   撑杆、绳索和悬绳连接的O点受到三个力作用而保持平衡，这三个力分别是：悬挂钢球的悬绳产生的向下拉力F₁、绳索的拉力F₂和撑杆的支撑力F₃。在这三个力中，F₂和F₃的合力R应该跟F₁大小相等，方向相反。因此根据题意将R分解后即可求得F₂和F₃的大小。

取1厘米长的线段为标度，表示200牛，在竖直方向上作线段BO＝2厘米，表示力R＝400牛，完成平行四边形ABCO，使∠AOB＝θ₁＝45°，∠BOC＝θ₂＝75°[图4-59（b）]。用标度量度OC，得F₂＝330牛；量度OA，得F₃＝450牛。所以绳索的拉力是330牛，撑杆的支撑力是450牛。

【例题2】

用弹簧秤沿着光滑斜面的方向将一块所受重力为5牛的木块匀速向上拉，这时弹簧秤上的读数是1.4牛，求斜面对木块的弹力的大小。

解   木块受到的重力G和弹簧秤的拉力F以及斜面的弹力N，都可看成作用在木块的重心上。已知木块保持匀速直线运动，所以G、F和N是三个共点的平衡力。因此，弹力N应该跟G和F的合力R大小相等、方向相反。

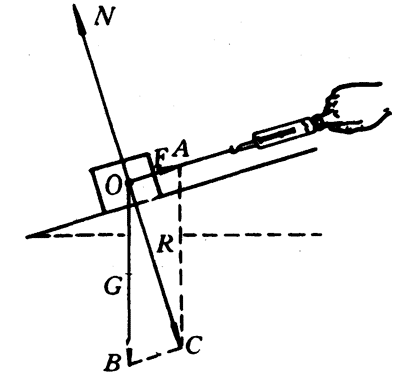
从图4-60的力图上可以看出，在表示F、G和R的线段OA、OB和OC所组成的平行四边形中，△OBC是直角三角形，所以

OC²＝OB²－BC²，

即                                       R＝\(\sqrt {{G^2} - {F^2}} \)＝\(\sqrt {{5^2} - {1.4^2}} \)牛＝4.8牛，

N＝R＝4.8牛，

斜面对木块的弹力的大小是4.8牛。

问题探讨

S：在解题时，力的合成、分解和平衡，不就是同一回事情吗？

T：它们不是一回事。力的合成、分解是一种方法；平衡是一种状态，平衡有一定的条件。但是，在几个共点力平衡的情况下，其中任一个力一定跟另几个力的合力大小相等、方向相反，因而在解决平衡问题时，也可以用力的合成或力的分解作为方法去取得结论。

思考

1．风筝在重力、风力和绳子的拉力共同作用下保持平衡。已知绳子与水平方向成30°角斜向下方，绳子对风筝的拉力是20牛。如果绳子突然断了，你知道这时的重力和风力的合力多大？方向怎样？

2．静止在斜面上的物体，是在重力跟哪几个力的共同作用下，保持平衡状态的？如果知道斜面的倾角θ，你能利用力的分解和力的平衡，求出这几个力的大小跟重力之间的关系吗？

练习二十三

1．将一个受10牛重力作用的砝码放在水平桌面上，用4牛竖直向上的力提住，这时桌面对它的支持力是多少牛？用3牛的推力，沿与水平夹60°角斜向下的方向去推一块放在水平桌面上的木块，木块没有被推动。已知木块所受重力是10牛，木块受到桌面的支持力和静摩擦力各是多少牛？

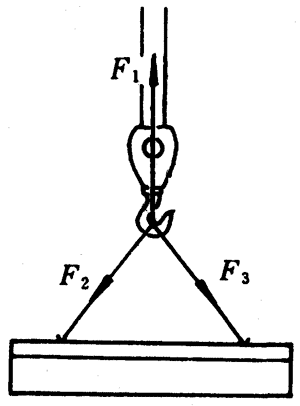
2．起重机将重物匀速吊起时，吊钩受到向上的牵引力F₁，它通过两根斜向的钢索悬住重物，两根钢索间的夹角为60°，钢索对吊钩的拉力F₂和F₃大小相等（图4-61）。如果已知F₁＝2.0×10⁴牛，求每根钢索对吊钩的拉力。

3．一个骑自行车的人，驶上倾角为15°的斜坡，人和车共受重力700牛，同时受到20牛平行于斜坡向下的阻力，那么，这辆自行车匀速上坡时，沿斜坡方向向上的动力需多大？

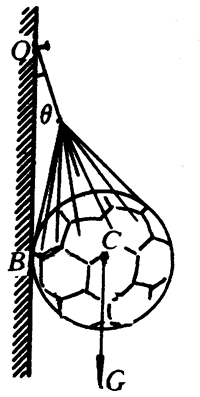
4．沿光滑的墙壁，用轻质网兜在O点挂着一只足球，足球所受重力是G，绳子与墙壁间的夹角是θ，球与墙壁的接触点为B（图4-62），求绳子对网兜的拉力和墙壁对球的弹力。

阅读材料  上海南浦大桥

为了开发浦东，加强和方便浦江两岸的经济文化和人民生活的联系，建造了上海南浦大桥（图4-63）。坐落在市区的南浦大桥由主桥、主引桥和分引桥组成。主桥是一跨过黄浦江的双塔双索面斜拉桥，全长846米，采用钢梁与钢筋混凝土板相结合的叠合梁结构，中孔跨径为423米，利用桥塔伸出的高强度斜拉钢索作为主梁的支承，用它代替中间桥墩。在当今世界同类桥梁中，南浦大桥的跨度仅次于西班牙的罗那桥和加拿大的安娜西斯斜拉桥，堪称世界第三大斜拉桥。

在黄浦江的东、西两岸，各设有一座宽7米、厚5米、高150米的折线式“H”型钢筋混凝土结构的桥塔，塔座基础选用直径900毫米、深达50余米的钢管桩群桩基础。每座桥塔两侧各以22对钢索连结主梁，索面成扇形布置。主桥高50米，通航净高46米，可通航5万吨级的巨轮。主桥桥面宽度为30.35米，它包括6个机动车道和两个2米宽的观光人行道。

南浦大桥东西两侧设置的引桥全长为7500米，采用预应力钢筋混凝土梁体和钢筋混凝土的墩台结构。浦西侧引桥长3754米，采用复曲线并呈螺旋形，主引桥的圆环直径为220米，绕行一圈半后，上下分两环分岔衔接中山南路和陆家浜路。衔接陆家浜路的分引桥为双向四车道，衔接中山南路的分引桥为双向八车道。浦东侧引桥长3746米，主引桥沿着桥位向东跨过浦东南路直通杨高路，以后，将继续向东延伸至规划中的东海之滨第三国际机场。分引桥则集中于主桥北侧，采用两个复曲线长圆环，绕行半圈后，与浦东南路上下行车道相接。

南浦大桥以优美的造型、独特的风格、刚劲挺拔的雄姿，呈现在人们的面前，它已成为上海一个重要的游览观光的景点，它的斜拉钢索，大跨主梁“H”型桥塔和螺旋形、低坡度引桥都充分体现了我国桥梁工程力学方面的重大成就（课本彩图10）。

本章学习要求

1．理解力的概念。

2．会用图示法表示力。

3．理解重力。

4．理解弹力产生的条件和弹力的方向。

5．常识性了解静摩擦力和最大静摩擦力。

6．理解滑动摩擦力，理解动摩擦因数。

7．知道物体受力情况的分析。

8．知道共点力。

9．理解合力和力的合成。

10．会用力的平行四边形定则求合力。

11．理解分力和力的分解。

12．会用力的平行四边形定则求分力。

13．理解共点力作用下物体的平衡条件。

复习题

1．要使所受重力为5000牛的木材在雪地上作匀速滑动，必须用175牛、沿水平方向的力去拖它，求木材与雪地间的动摩擦因数。

2．放在斜面上的物体，在斜面倾角θ有所增大时，如果物体仍能保持静止不下滑，下面几种说法中正确的是（     ）

（A）由于重力沿斜面方向的分力F₁增大时，物体受到的静摩擦力也增大

（B）由于重力使物体压紧斜面的分力F₂增大，物体受到的静摩擦力就增大

（C）由于重力和静摩擦力都没有变化的缘故

3．用作图法把一个20牛的力分解成两个40牛的分力，求这两个分力间的夹角。

4．在一直线上的5牛、10牛、14牛三个力，在什么情况下它们的合力最大？什么情况下它们的合力最小？最大值和最小值各等于多大？

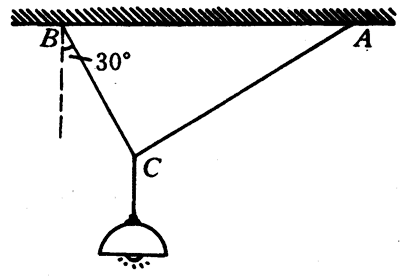
5．如图4-64所示，用一端固定在天花板上的细绳AC将原来竖直悬挂电灯的线拉开，使线与竖直方向偏离30°角。如果灯所受重力为5牛，细绳AC上的拉力是2.5牛，试用作图法求出电线BC段所受拉力的大小和细绳AC的方向。

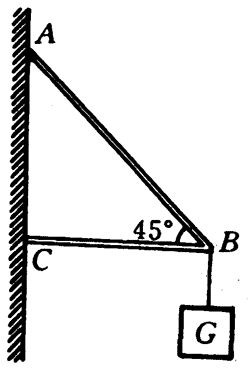
6．如图4-65所示，支架的轻质横梁即是水平的，拉杆AB跟横梁成45°角，在支架的端点B处挂上所受重力为800牛的物体，横梁和拉杆各受到多大的作用力？它们的方向怎样？用计算法求解。

7．有人说：倾角为θ的光滑斜面，放上物体时，物体受到的合力总是等于Gsinθ。你认为对吗？对吗？试分别用力的分解和合成来证明。

8．滑雪运动员所受重力为700牛，他沿着山坡滑下。山坡的倾角是30°，滑雪板和雪坡之间的动摩擦因数是0.04，求滑雪运动员所受到的合力。

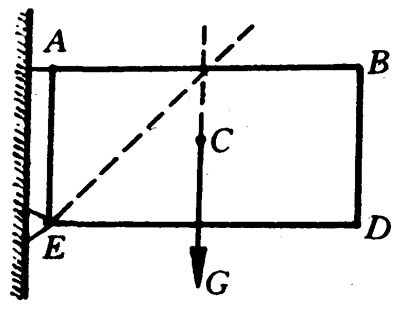
9．一块长0.4米，宽0.2米的薄木板，它的左下角E用光滑铰链连接在竖直墙上，左上角A用一段铁丝沿水平方向拉住（图4-66）。薄木板所受的重力为10牛，作用在它的重心C上，求铁丝和铰链对木板的拉力和支持力的大小和方向。（提示：薄木板所受的铁丝拉力、铰链支持力和重力的作用线通过同一点。）

10．跳伞空降的人，由于受到水平方向的风力而沿着和竖直方向成30°角的方向匀速下降，如果人和伞共受重力为700牛，求他降落时所受的空气阻力。

发布时间：2015/9/26 下午10:52:59  阅读次数：2550