七、力的分解

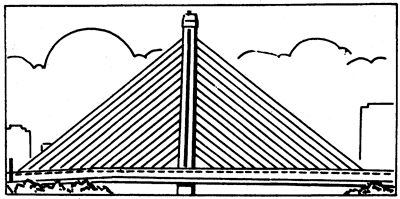
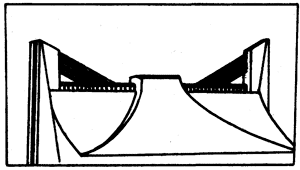
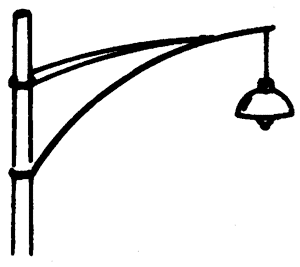
架设在上海恒丰北路上跨越铁路的斜拉桥（图4-40），是我国第一座预应力混凝土独塔单索面斜拉桥，全长614米，矗立的桥塔两侧各有30根钢索拉住桥面，形成竖琴式结构。每侧钢索在空间的排布都是平行、等距的，它们分担着桥面的自重以及通过车辆和行人时的负载，实质上，这是一种支架结构。我们只要留意观察，还会看到一些建筑物上也有类似结构，如北京国家奥林匹克体育中心的顶棚，采用双柱式支架结构，每侧用8根平行钢索拉住（图4-41）。最简单的这类支架结构就像马路上的路灯支架（图4-42），它是由固定在立柱上的拉杆和撑杆所组成的。由于路灯受到重力的作用，它对支架端点有向下的拉力，支架承受了这个拉力，悬住了路灯。为了研究上述斜拉桥和顶棚上的拉索是怎样起到分担力的作用的，路灯支架为什么要采取这样的结构，支架的拉杆和撑杆在悬住路灯时，分别受到什么方向的力的作用等等问题，就必须学习有关力的分解的知识。

力的分解

把一个已知力分成几个分力叫做力的分解。最简单的情况，是在已知力的作用点上，把这个力分解成两个共点力。

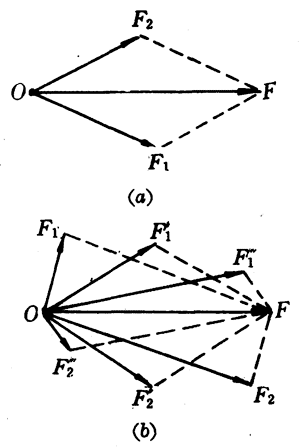
把一个力分解成两个共点力是共点力合成的逆运算，也遵循平行四边形定则。就是说，如果把已知力F作为某个平行四边形的对角线，那么这个平行四边形的两个邻边就表示两个分力F₁和F₂[图4-43（a）]。

但是，如果没有其他条件，同一对角线，可以作出无数个不同的平行四边形，那么一个已知力F就可以被分解成无数对大小、方向不同的分力[图4-43（b）]。因此，一个已知力究竟应该怎样分解，就必须附带一定的条件，这些条件是根据力的实际作用效果来决定的。现在我们就通过对几个典型例子的分析来进行研究。

斜面上物体所受重力的分解

骑自行车下桥时，不必用力蹬踏，自行车会自动从桥顶驶下，而且桥坡越陡，向下冲得就越快（图4-44）。这是什么原因？是不是重力在起作用呢？我们可以用下面的实验来进行研究。

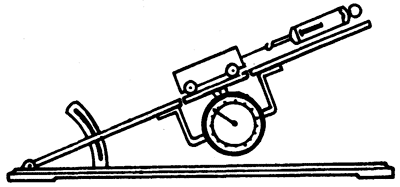
把一块中间开槽的光滑木板，平放在水平桌面上，把一辆实验小车放在木板上，由于小车受到的重力被木板的支持力（弹力）所平衡，小车将保持静止不动。如果把木板的一端抬高，成为斜面，小车就会沿着斜面下滑，同时紧压着斜面，显然这时重力不能被木板的支持力所平衡。这时如果用一个弹簧秤从斜面顶端，通过细绳拉住小车，再把—个圆盘测力计固定在木板下面，从木板的槽孔中支住小车（图4-45），我们就会清楚地看到弹簧秤和圆盘测力计上都显示出读数，它们分别表明放在斜面上的物体所受重力的两个作用效果，即一方面使物体沿斜面下滑，另一方面又使物体紧压在斜面上，对斜面产生压力。因此，根据实际作用效果，重力G应该按照平行于斜面方向和垂直于斜面方向分解成两个分力。图4-46就是物体所受重力分解成这两个方向分力的示意图，其中F₁是物体所受重力平行于斜面方向的分力，它的作用是使物体沿斜面下滑。F₂是物体所受重力垂直于斜面方向的分力，它的作用是使物体紧压斜面，对斜面产生压力。实验证实了F₁和F₂的合力也就是重力G。

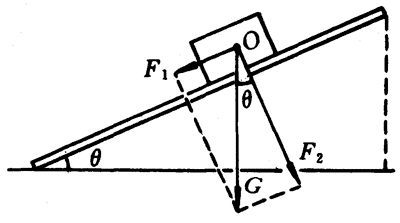
如果已知斜面的倾角θ，就可以求出分力F₁和F₂的大小。即

F₁＝Gsinθ，F₂＝Gcosθ。

从这两个计算式中可以看出，F₁、F₂的大小跟斜面的倾角θ有关，斜面的倾角θ越大，F₁越大，F₂越小。如果改变图4-45所示实验装置中斜面的倾角，就可以从弹簧秤和圆盘测力计上分别读出F₁和F₂的大小，根据读数的变化来加以验证。

桥坡也是一个斜面，车辆上桥时，重力的分力F₁会阻碍车辆前进；车辆下桥时，分力F₁会使车辆运动加快。为了减小车辆上坡时所需的牵引力，为了下坡时行车的安全，在设计桥梁时，引桥都做得很长，或者采用螺旋形的引桥，以减小桥的坡度，使倾角θ变小，F₁不致过大。例如上海南浦大桥浦西引桥采用双螺旋结构，引桥的最大坡度不超过4%。盘山公路（本章导图4）都修筑得曲曲折折也是这个道理。

塔吊吊臂端点所受拉力的分解

塔吊（本章导图1）在吊住货物时，货物通过悬绳使吊臂端点受到竖直向下的拉力F，F的大小等于货物所受重力G[图4-47（a）]。拉力F对塔吊上的钢索和水平吊臂将产生怎样的作用呢？

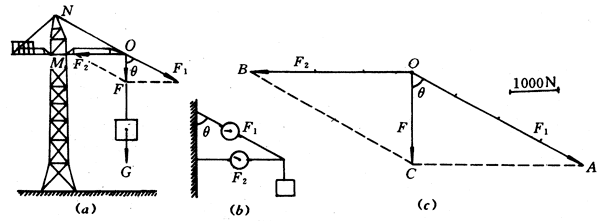
如果用细绳代替钢索，用轻质木杆代替吊臂，制作一个支架模型，并在绳间和杆间分别接入圆盘测力计，把它们固定在铁架台上。然后在支架端点挂一重物，从两个圆盘测力计的指针偏转方向就可以看出，细绳受到拉力作用，而轻质木杆则受到压力作用[图4-47（b）]。这就形象地表明：塔吊吊住货物，吊臂端点受到向下拉力F作用时，它的钢索就受到沿NO方向的拉力F₁，吊臂就受到沿OM方向的压力F₂。F₁和F₂是吊臂端点受到力F作用时产生的，因此F₁和F₂是F的两个分力。

这两个分力的大小可以按平行四边形定则，用作图法来确定。

如果图4-47中吊住的货物重2000牛，钢索NO与竖直方向的夹角θ＝60°。用1厘米长的线段为标度，表示1000牛。先沿竖直方向作出拉力F，然后根据平行四边形定则完成平行四边形OACB[图4-47（c）]，使∠AOC＝60°，这时线段OA和OB就分别表示分力F₁和F₂，根据标度，即可量得F₁＝4000牛，F₂＝3450牛。

因为∠NMO是直角，△AOC∽△ONM，所以也可以用F₁＝F/cosθ，F₂＝Ftanθ，计算出F₁和F₂的大小。

从上述两个例子的分析中可以知道：在力的分解时，首先要从实际出发，研究这个力有哪些作用效果，然后找出具体条件，并根据条件进行分解，才能得到正确解答。

力的合成和分解在工程技术方面有着重要的现实意义，例如桥梁的建筑。从我国古代的拱桥（本章导图2）到现代的斜拉桥，都是利用了力的合成和分解原理，把桥面所受的力，分担到桥墩和塔柱上去的。

思考

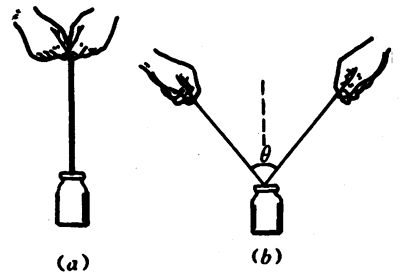
1．一根细线可以挂住一个大砝码，如果把这个砝码挂在这根细线的中央[图4-48（a）]夕拉开细线两端[图4-48（b）]，当两段细线之间的夹角θ增大到一定程度时，细线拉断了，这是什么原因？

2．甲、乙两位同学体重相同，在单杠上做引体向上的动作时，甲两臂张开成10°角，乙两臂张开成30°角，哪位同学手臂的拉力大些？

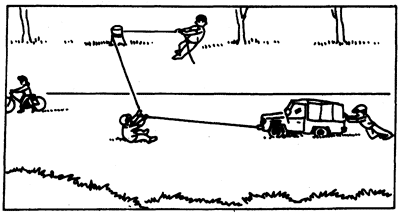
3．有经验的司机为了把陷在泥坑里的汽车拉出来，常用一根结实的绳子，把它的两端分别拴住汽车和绕住树桩，然后一面在绳子的中央用力拉绳子（图4-49），使两段绳子的夹角大于120°，一面不断收紧绕在树桩上的绳子，并在轮子下面填进石块或木板，这样就可以用较小的力逐步把汽车拉出泥坑。你能说出其中的道理吗？

练习二十二

1．根据力的平行四边形定则，把一个已知力分解成两个分力，每个分力都跟原来的力成60°角，这两个分力的大小跟原来的力有什么关系？

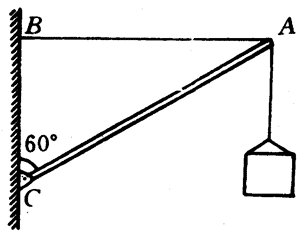
2．用绳索和轻质撑竿吊起所受重力为750牛的箱子，在绳索AB水平、轻质撑竿AC跟竖直方向成60°角时（图4-50），绳索AB和撑竿AC各承受多大的力？方向怎样？

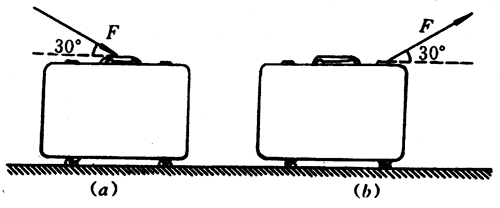
3．装有小轮的箱子所受重力为150牛，放在光滑的水平地面上。人们用大小为50牛、跟水平方向成30°角的力去推它或者拉它[图4-51（a）、（b）]，求在这两种情况下，该力在水平方向上，使箱子前进的分力和在竖直方向上的分力跟重力的合力。

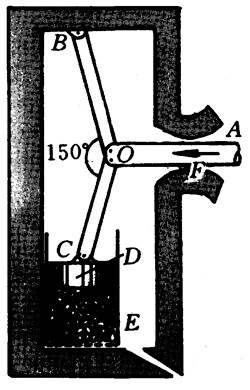
4．图4-52是一种压榨机的示意图，OA是推杆，OB和OC是挺杆，O、B、C处都以铰链相接，D为压块，E为有孔容器。当以水平力F作用于推杆时，OC挺杆就会有力作用于压块D，使它紧压容器E中的物体。如果F＝20牛，∠BOC＝150°，试用作图法求沿挺杆OC的作用力F_C的大小。

5．圆柱体所受重力为100牛，放在光滑的竖直平面和斜面之间。如果已知斜面的倾角θ＝30°（图4-53），试求重力沿垂直于两个接触面方向上的分力。

发布时间：2015/9/26 下午10:29:23  阅读次数：1386