六、力的合成

在日常生活、交通运输和工农业生产中，作用在物体上的力往往不止一个。例如，教室里用两根细链悬挂一盏日光灯；造船厂在安装大型远洋货轮的尾部或驾驶舱时，常常需要用两台大吊车同时吊装等。下面我们就来研究物体受到几个力共同作用时的情形。

力的合成

在黄浦江上，有时会看到用几条拖轮牵引驳船的情形。1990年12月2日上海报载：一架长78.2米、宽24.6米、高3.5米、重1080吨的苏州河闸桥的中跨钢梁，在8艘拖轮的拖带下，由黄浦江顺利地穿越外白渡桥进入苏州河（图4-29）。这是由于中跨钢梁既大又重，一条拖轮的牵引力太小，所以采用多条拖轮来牵引。但就一般情况来说，我们自然很容易想到，是不是可以用一条牵引力足够大的拖轮来代替，这样也就不会影响航道上其他船只的通行了。显然，在这里用一条拖轮牵引时，它的作用效果应该跟原来用多条拖轮牵引时的效果等同。如果这一设想能够实现，那么就可以把这一条拖轮的牵引力叫做那几条拖轮的牵引力的合力，而原来那几条拖轮的牵引力就叫做分力。因此合力和几个分力的作用是等效的，它们是可以相互替代的。

求几个已知力的合力，叫做力的合成。

共同作用在一个物体上的力，它们的大小和方向可以不同，它们的作用点，可以在物体的同一点上，也可以不在同一点上。我们把作用在物体的同一点上，或者力的作用线可以相交在同一点上的力，叫做共点力。

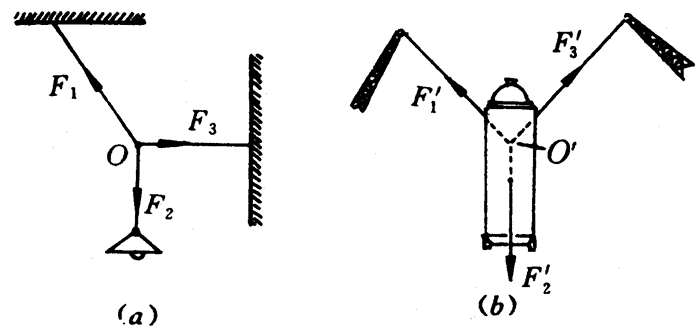
图4-30（a）中，悬挂电灯的电线与水平拉绳的结点O处受到三个力的作用：F₁、F₂和F₃，这三个力是共点力。在图4-30（b）中，用两台起重机吊着的化工厂的分馏塔受到F₁ʹ、F₂ʹ和F₃ʹ三个力的作用，这三个力的作用点虽然不在同一点上，但是三个力的作用线都相交在Oʹ点，所以它们也是共点力。

力的平行四边形定则

共点力的合力和分力在大小和方向上有怎样的关系呢？我们用图4-31（a）所示的实验装置来研究。把一根橡皮绳的A端固定在贴有白纸的竖直板上，B端与两根细绳相连，两根细绳的另一端分别跨过两个定滑轮后再挂上钩码，两个滑轮可以在竖直板上的弧形槽内移动并可固定下来。实验时，在两根细绳末端挂上不同数目的钩码，调节滑轮C和D的位置，使橡皮绳B端沿竖直方向伸长到Bʹ点，把滑轮固定下来，在纸上沿细绳画出它们的方向，记下它们所挂的钩码数。取去两根细绳，改用一根细绳挂上适量的钩码，使橡皮绳的B端仍沿着竖直方向伸长到Bʹ点，发生相同的形变，记下这时细绳上所挂的钩码数。

在白纸上标出O点，表示橡皮绳B端所在位置Bʹ（力的作用点），选定一个钩码所受重力的大小为标度，沿原来两根细绳的方向作出线段OP、OQ，则OP、OQ分别表示原来两根细绳的拉力（即分力）F₁、F₂，再沿竖直方向作出线段OR，表示后来用一根细绳时的拉力（即合力）F，然后依次用虚线连接PR和QR[图4-31（b）]，可以看出OPRQ是一个平行四边形。

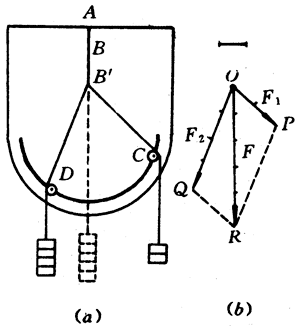
可见，两个互成角度的共点力的合力，可以用表示分力F₁、F₂的线段OP、OQ为邻边，作出的平行四边形的对角线来表示，对角线的方向正好跟合力的方向相同，对角线所表示的力的大小，正好等于合力F的大小。

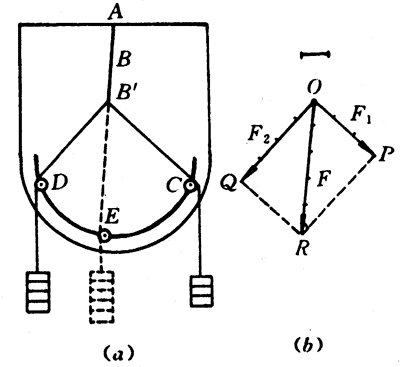
我们可以重做一次实验：使橡皮绳B端在两个力作用下沿斜向伸长到Bʹ点[图4-32（a）]，然后改用一根细绳跨过滑轮E，挂上钩码，钩码产生的拉力使橡皮绳B端也沿斜向伸长到Bʹ点，记下实验中得到的数据，也可以用表示力F₁、F₂和F的线段作出一个平行四边形[图4-32（b）]，从而得到跟前面实验相同的结果。大量实验证明：无论怎样改变共点力F₁、F₂的大小和它们之间的夹角，同样可以得到上述的结果。

互成角度的两个共点力的合力，可以用表示这两个力的有向线段作邻边画成的平行四边形的对角线表示。这就是力的平行四边形定则。

不但是力，所有矢量（如位移、速度和加速度等）的合成也都遵循平行四边形定则。平行四边形定则也是矢量加减运算的定则。

如果我们在做实验时，保持两根细绳上所挂的钩码数不变，而改变滑轮位置，使两根细绳间的夹角变小，我们就会发现橡皮绳将伸得更长，说明两根细绳拉力的合力增大[图4-33（a）]。相反，如果增大两绳间的夹角，橡皮绳的伸长量就会减小，说明两根细绳拉力的合力减小[图4-33（b）]。这就表明在分力F₁和F₂的大小不变时，它们的合力F的大小跟两个分力之间的夹角θ的大小有关：夹角减小，合力变大；夹角增大，合力变小。

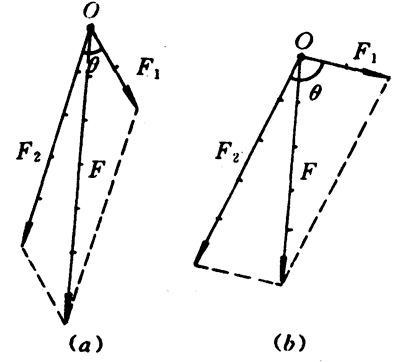
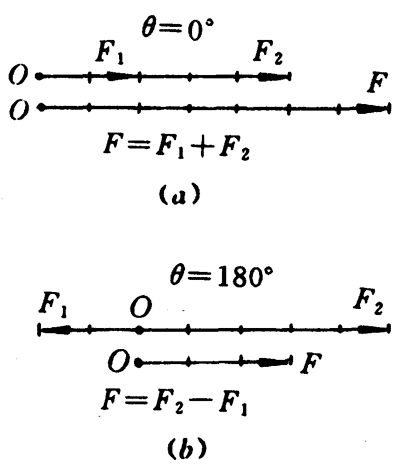
当两个分力在同一直线上，方向相同，即它们的夹角θ＝0°时，合力的大小等于两个分力大小之和，合力的方向和两个分力方向相同[图4-34（a）]。当两个分力在同一直线上，方向相反，即它们的夹角θ＝180°时，合力的大小等于两个分力大小之差，合力的方向和分力中数值大的那个分力的方向相同[图4-34（b）]；如果这两个分力的大小F₁＝F₂，那么合力F＝0。

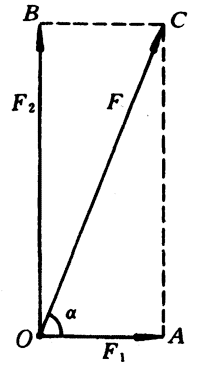
当两个分力F₁和F₂之间的夹角θ＝90°，那么用表示分力F₁和F₂的有向线段所作出的平行四边形就成为一个矩形（图4-35），合力F的大小和方向，可以用以下的式子来计算和表示：

F²＝F₁²＋F₂²，tanα＝\(\frac{{{F_2}}}{{{F_1}}}\)

【例题1】

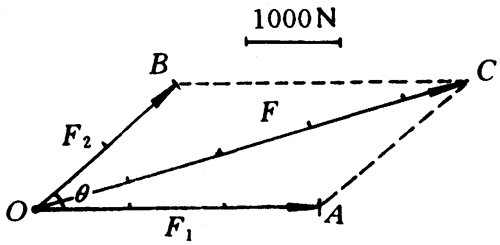
有两条拖轮牵引一艘驳船，它们的牵引力分别是F₁＝3000牛，F₂＝2000牛，牵绳之间的夹角θ＝40°。假如只用一条拖轮来牵引，而产生的效果跟原来的相同，试用作图法求出这条拖轮的牵引力F的大小和方向。

解   这一条拖轮的牵引力，实际上就是原来两条拖轮牵引力的合力。选定1厘米长的线段代表1000牛，以O点为作用点，以2厘米长的线段OB和3厘米长的线段OA分别表示拉力F₂和F₁，并使它们的夹角θ＝40°。以F₁和F₂为相邻的两个边作平行四边形，然后从O点作平行四边形的对角线OC，OC即为代表合力F的有向线段（图4-36）。量得对角线OC的长为4.7厘米，用量角器量得F与F₁的夹角为16°。所以，F₁和F₂的合力F，也就是这一条拖轮的牵引力，它的大小等于4700牛，方向与拉力F₁所成夹角等于16°。

【例题2】

用绳悬住的重物，所受重力是40牛。现在用30牛的拉力，沿水平方向把它拉开[图4-37（a）]，求重物所受重力和拉力的合力。

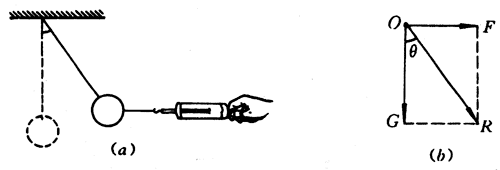
解   按题意运用平行四边形定则作出力F、G和它们的合力R的示意图，如图4-37（b）。可以看出表示F、G和R的线段分别是直角三角形的两条直角边和斜边。根据勾股弦定理和三角函数关系，得合力

R＝\(\sqrt {{F^2} + {G^2}} \)＝\(\sqrt {{{30}^2} + {{40}^2}} \)牛＝50牛，

tanθ＝\(\frac{F}{G}\)＝\(\frac{{30}}{{40}}\)＝0.75，θ＝36.9°

即合力是50牛，与竖直方向成36.90夹角。

两个以上共点力的合成，可以用逐步合成的方法，先用平行四边形定则求出其中任意两个力的合力，再以这个合力跟第三个力求合力，依次类推，直到把所有的力都合成完，最后求得的合力就是这些力的合力。

思考

1．两人合提一个水桶，每人所用的力一定比一个人独自提水桶用的力小吗？为什么？

2．两个大小相等的共点力，在它们之间的夹角由0°变到180°的过程中，合力的最大值和最小值相差多大？

等效替代的方法

等效替代是研究物理学常用的方法。在初中学习电学知识时，已经知道电阻串联时的总电阻大于任一个串联电阻的阻值，等于各串联电阻之和。因此，在进行电路计算时，可以把串联电路中各部分的总电阻看成是一个电阻，而其阻值就等于各串联电阻的阻值之和，这样便可简化电路。这就是一种等效替代的方法。电阻并联时总电阻将小于任一分路的电阻，总电阻的倒数等于各分路电阻的倒数和。在电路中如有若干电阻并联（如家庭电路中各家用电器的连接），也可看成电路中只有一个电阻，这个电阻的倒数就等于各分路电阻的倒数和。这也是一种等效替代。

在物体受到多个力作用时，只需求出物体所受的合力，然后研究物体在这个合力作用下运动状态可能发生的变化，这同样可以简化问题。等效替代的方法在今后的学习中还会多次用到。

练习二十一

1．两个共点力大小都等于9牛，互成120°角，用作图法求它们的合力，比较一下合力跟分力的大小，并看看这个合力的方向跟两个分力方向间的夹角有什么关系？

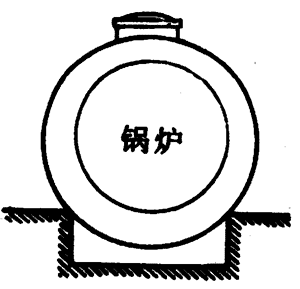
2．把一只圆柱形锅炉放在两个砖砌的支墩上（图4-38），已知两个支墩对锅炉的支持力分别作用于它们跟锅炉的接触处，力的作用线都指向锅炉截面的圆心，并且相互垂直，它们的大小各是2000牛，试求这两个支持力的合力。

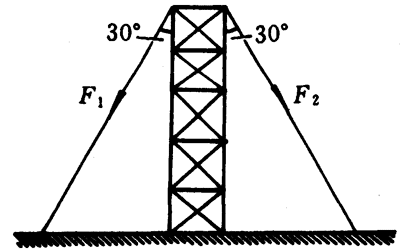
3．为了防止支架倾倒，在它的两侧对称地用钢丝绳拉紧，并且固定在地面上。如果钢丝绳与竖直方向的夹角为30°（图4-39），它们的拉力F₁和F₂的大小都等于300牛，试求它们的合力。

>

4．两个小孩分别用12牛向东的力和5牛向南的力，去拉一块放在水平桌面上的木块，两力都平行于桌面，这时木块所受合力多大？方向如何？

5．4牛和8牛的两个力，沿同一水平面作用于一个物体，它们的合力能够等于3牛、4牛、10牛、12牛、15牛吗？为什么？

发布时间：2015/9/26 下午10:06:10  阅读次数：1073