第七讲 电磁感应定律

电磁感应现象是电磁学中最重大的发现之一，它揭示了电与磁相互联系和转化的重要方面。电磁感应现象的发现在科学上和技术上都具有划时代的意义，它不仅丰富了人类对于电磁现象本质的认识，推动了电磁学理论的发展，而且在实践中开拓了广泛的应用前景。

在基础型课程中已讲过电磁感应现象和右手定则；拓展型课程Ⅰ中介绍了楞次定律、导线切割磁感线时感应电动势的定量计算式，本讲将逐步深入地讨论电磁感应现象中感应电动势与磁通量变化之间的定量关系，介绍法拉第电磁感应定律以及它的应用。

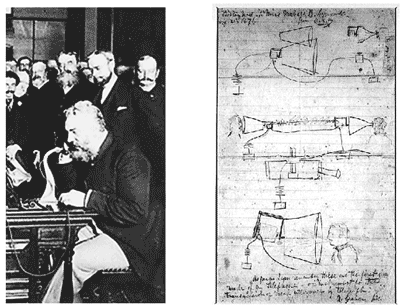
电话是利用电信号传输消息、互通话语的通信方式。美国发明家亚历山大·贝尔于1876年申请了电话发明的专利。1878年，贝尔成功地进行了在波士顿和纽约间的首次长途通话，图7-1（a）是贝尔在展示他的电话机，图7-1（b）是贝尔画的电话原理的草图。

在电话机的发话端，当有人在送话器前说话时，声波使膜片带动磁场内的线圈发生相应的振动，从而产生感应电流，把声音信号转变成电信号。很明显，线圈在磁场中随膜片振动时，穿过线圈的磁通量在不断地变化，感应电流的变化规律跟线圈随膜片的振动情况有关。可见电话机是电磁感应现象的一个应用实例。

在基础型课程和拓展型课程Ⅰ中，分别介绍了电磁感应现象、右手定则、楞次定律、导体切割磁感线时感应电动势E＝Blv，本讲将逐步深入地讨论电磁感应现象中感应电动势与磁通量变化之间的定量关系，介绍法拉第电磁感应定律以及它的应用。

一、影响感应电动势大小的有关因素

导体中感应电流的大小究竟跟哪些因素有关呢？下面我们通过实验来探究这个问题。

［学生实验］用DIS研究回路中感应电动势大小与磁通量变化快慢的关系

【实验目的】探索影响感应电动势大小的有关因素。

【实验器材】导轨、小车、挡光片、螺线管、磁铁、电压传感器、光电门传感器、计算机等。

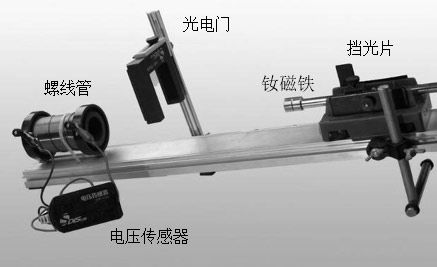
【实验装置】如图7-2所示，小车上装有磁铁和挡光片，小车的挡光片经过光电门传感器时，DIS实验系统记录挡光时间Δt，电压传感器记录下此段时间螺线管中感应电动势的平均值E。

【实验过程及数据分析】

（1）让小车以不同的速度靠近螺线管，得到在不同Δt内的感应电动势平均值E。（感应电动势平均值近似于最大值）

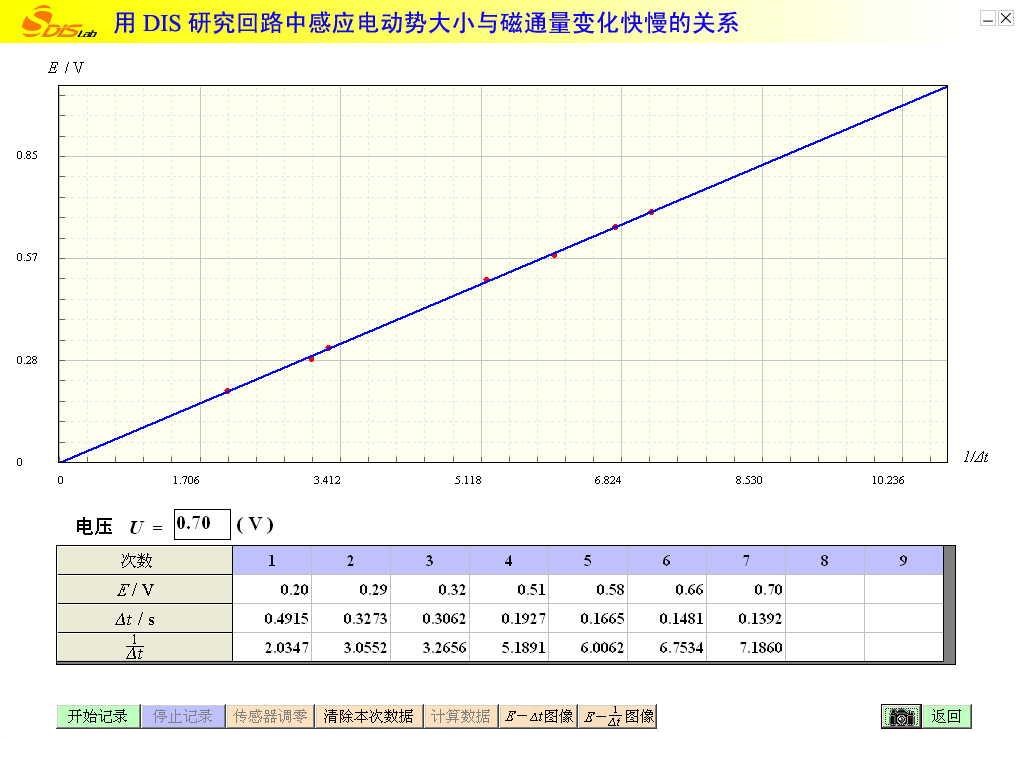
（2）重复上述步骤可得一组Δt和E值，点击软件界面上“E－$\frac{1}{\mathrm{\Delta }t}$”，屏幕出现图7-3所示图线。实验中因磁铁相对螺线管变化的位置相同，所以各次实验螺线管中磁通量的变化ΔΦ都相同，可见感应电动势E和$\frac{1}{\mathrm{\Delta }t}$成正比关系，即E和Δt成反比。

（3）改用不同匝数的线圈（线圈直径不变），使磁铁用相同速度靠近线圈，会得到什么结果？

【实验结果】

_______________________________________________________________。

二、法拉第电磁感应定律

通过DIS实验可以知道，感应电动势大小跟穿过回路的磁通量的变化快慢有关：磁通量变化越快，感应电动势越大。

感应电动势大小跟磁通量变化快慢的定量关系如何？

我们把单位时间里穿过回路的磁通量的变化量，叫做磁通量的变化率。因此，上述实验告诉我们：感应电动势的大小跟穿过电路的磁通量的变化率有关。

精确的实验结果表明，单匝线圈中感应电动势大小E跟磁通量的变化率$\frac{\mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }t}$成正比，即

E＝k·$\frac{\mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }t}$。

这个定律是法拉第首先发现的，因而叫做法拉第电磁感应定律。

在国际单位制中，磁通量变化率的单位是Wb/s，感应电动势单位是V，此时k＝1，因而在国际单位制中法拉第电磁感应定律的数学表示式为

E＝$\frac{\mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }t}$。

大家谈

在国际单位制中，k为什么等于1？

在实际应用中，为了获得较大的感应电动势，都采用多匝线圈。若线圈的匝数为N，整个线圈中的感应电动势就等于单匝线圈的N倍（在DIS实验中已证实），那么

E＝N·$\frac{\mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }t}$。

在基础型课程中我们已经知道，有无电磁感应现象，要看穿过闭合回路的磁通量是否发生变化；法拉第电磁感应定律则告诉我们，感应电动势的大小决定于磁通量的变化率；根据闭合电路欧姆定律可知，感应电流的大小，不仅与感应电动势有关，还与电路的电阻有关。

历史回眸

法拉第于1831年发现了电磁感应现象后，与1832年建立了电磁感应定律。但是，现在所采用的数学表达式，是1846年诺埃曼和韦伯通过各自的研究而总结出来的。由于法拉第的杰出贡献，定律仍以他的名字命名。

【示例1】一个200匝的线圈，在0.02 s内线圈中磁通量的变化量为6×10^-5 Wb。求线圈中感应电动势的大小。

【解答】已知Δt＝0.02 s，ΔΦ＝6×10^-5 Wb，N＝200匝，根据法拉第电磁感应定律，线圈中感应电动势大小为

E＝N·$\frac{\mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }t}$＝$\frac{200\times 6\times {10}^{-5}}{0.02}$V＝0.6V。

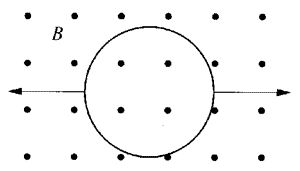
【示例2】匀强磁场垂直于纸面向外，磁感应强度B＝2×10^-2 T。一个直径为20 cm、电阻为0.1 Ω的圆线圈放在磁场中，线圈平面垂直磁场方向，在线圈某一直径两端用力拉线圈（如图7-4所示），在0.5 s内使线圈面积变为零，问在这个过程中线圈内感应电流方向如何？平均感应电流多大？

【解答】（1）用力拉线圈的过程中，线圈面积减少，虽然磁感应强度未变，但穿过线圈的磁通量在减小，因而感应电流的磁场方向跟原磁场方向相同，由安培定则可知感应电流是沿逆时针方向的。

（2）感应电流大小与感应电动势、电阻大小有关。先求出平均感应电动势

E＝$\frac{\mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }t}$＝$\frac{B\cdot \mathrm{\Delta }S}{\mathrm{\Delta }t}$

＝$\frac{2\times {10}^{-2}\times 3.14\times {0.1}^2}{0.5}$V

≈1.26×10^-3 V。

然后，可以求出感应电流的平均值

I＝$\frac{E}{R}$＝$\frac{1.26\times {10}^{-3}}{0.1}$A＝1.26×10^-2A。

点击

根据法拉第电磁感应定律E＝$\frac{\mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }t}$得到的是Δt时间内感应电动势的平均值。

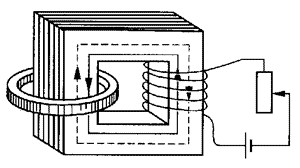
【示例3】如图所示，铁芯右边绕有一个线圈，线圈两端与滑动变阻器、电池组连成回路。左边的铁芯上套有一个半径为0.1m、电阻为0.1Ω的金属环，铁芯的横截面积为0.01m²，且假设磁场全部集中在铁芯中。调节滑动变阻器的滑动头，使铁芯中的磁感应强度每秒增加2×10^-3T。求金属环中感应电流的大小和方向。

【分析】滑动变阻器电阻的变化，改变了右边线圈中电流的大小，使铁芯中的磁场增强，其变化率为（$\frac{\mathrm{\Delta }B}{\mathrm{\Delta }t}$）；同时还要注意，计算磁通量的有效面积（S），必须是磁场实际存在的区域面积，所以应选取铁芯的截面积作为S，而不是左边金属环的面积。然后，再用楞次定律判断出感应电流的方向。

【解答】金属环中的感应电动势

E＝$\frac{\mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }t}$＝S·$\frac{\mathrm{\Delta }B}{\mathrm{\Delta }t}$＝0.01×2×10^-3 V＝2×10^-5 V。

I＝$\frac{E}{R}$＝$\frac{2\times {10}^{-5}}{0.1}$A＝2×10^-4A。

感应电流方向的判断：铁芯中原磁场方向如图中实线所示；磁场增强，则感应电流磁场的方向跟原磁场方向相反，如图中虚线所示；用安培定则判定金属环中感应电流方向是逆时针方向（俯视）。

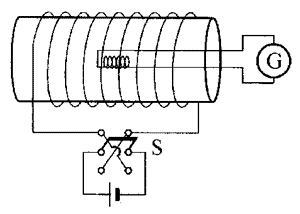
【示例4】在图中，已知小探测线圈有2 000匝，线圈的直径为2.5 cm，整个串联回路的电阻是1000 Ω，当开关S反向时测得ΔQ＝2.5×10^-7 C。求被测处的磁感应强度。

【分析】当反向开关S使螺线管里的电流反向流动时，穿过小线圈的磁通量的变化量是ΔΦ＝2BS，产生的感应电动势E＝$\frac{\mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }t}$，感应电流I＝$\frac{E}{R}$。用上列几个关系式就可以求得答案。

【解答】感应电流I＝$\frac{E}{R}$＝$\frac{N\frac{\mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }t}}{R}$，因I＝$\frac{\mathrm{\Delta }Q}{\mathrm{\Delta }t}$，可得

ΔΦ＝R·$\frac{\mathrm{\Delta }Q}{N}$；

根据分析可知，ΔΦ＝2BS，就能得出下列关系式：

B＝R·$\frac{\mathrm{\Delta }Q}{2NS}$，

代入题中所给的数据进行计算：

B＝$\frac{1000\times 2.5\times {10}^{-7}}{2\times 2000\times 3.14\times {(1.25\times {10}^{-2})}^2}$T≈1.27×10^-4 T。

通过计算就可以知道长螺线管中起“探头”作用的小线圈所在处的磁感应强度。

在电工技术中，运用电磁感应原理制造的发电机、感应电动机和变压器等电器设备为充分而方便地利用自然界的能源提供了条件；在电子技术中，广泛地采用电感元件来控制电压或电流的分配，发射、接收和传输电磁信号；在电磁测量中，除了许多重要电磁量的测量是直接应用电磁感应原理外，一些非电磁量也可以通过电磁感应转换成电学量来测量，从而发明了多种自动化仪表。

三、电磁感应现象中能量的转化

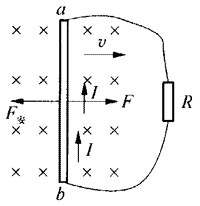
在电磁感应现象中，产生感应电动势的那部分导体相当于电源。如图7-7所示，ab导体向右运动时，有b→a方向的感应电流。在磁场中，通电导体ab要受到向左的安培力作用，为了维持它做匀速运动，必须有跟安培力大小相等、方向相反的外力克服安培力做功，在做功的过程中，机械能转化为电能。所以，电磁感应现象也符合能的转化和守恒定律。

自主话动

你能从能的转化和守恒定律推导出关系式E＝BLv吗？

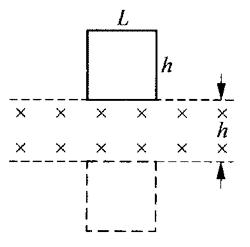
【示例5】如图7-8所示，边长分别为L、h，电阻为R，质量为m的矩形金属线框，自上而下匀速穿过宽度为h、磁感应强度为B的匀强磁场区域，求线框中产生的热量。

【解答】线圈匀速穿过匀强磁场的过程可分为两段：（1）线圈刚进入磁场到全部进入磁场；（2）线圈从磁场中全部离开。每个阶段磁通量的变化量都是ΔΦ＝BLh，时间Δt＝$\frac{h}{v}$，感应电动势

E＝N·$\frac{\mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }t}$＝BLv，

I＝$\frac{BLv}{R}$。

电流做功使机械能转变成内能，产生的热量

Q＝2I²RΔt＝$\frac{2B^2{L}^{2}vh}{R}$。                           ①

又因线框匀速运动，则

F＝BIL＝mg，

$\frac{B^2{L}^{2}v}{R}$＝mg。                                          ②

将②式代入①式得

Q＝2mgh。

如果换一个思路考虑，因为线框下落速度不变，动能不变，故线框中产生的热是由机械能（重力势能）转化为电能再转化为内能的，只要知道重力势能的减少，直接可得到答案：Q＝2mgh。

由此例可知，在电磁感应现象中用能的转化和守恒定律来解决实际问题，有时可以相当简捷。

四、导体切割磁感线时感应电动势大小的计算

用法拉第电磁感应定律能导出导体切割磁感线时产生的感应电动势大小吗？

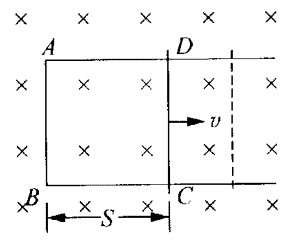
如图7-9所示，导体CD向右做（垂直）切割磁感线运动，运动速度为v，CD长为L，那么在时间Δt内导体移动距离是v·Δt。穿过回路的磁通量的变化量ΔΦ是BLvΔt。根据法拉第电磁感应定律，可得

E＝$\frac{\mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }t}$＝BLv。

应用上述公式计算导体切割磁感线时感应电动势的大小，在拓展型课程Ⅰ中已作了重点介绍。

点击

在拓展型课程Ⅰ中，从外力做功使能量发生转变的角度，推导出E＝BLv。因为法拉第电磁感应定律反映了能的转化和守恒的规律，所以用法拉第电磁感应定律来推导导体切割磁感线时感应电动势的大小，其结果也是E＝BLv。

发布时间：2015/9/23 下午4:04:35  阅读次数：2035