C 力的分解

图2-25中，一辆货车陷入路边泥洼中，依靠自身动力无法脱身。只见司机用钢索将汽车与路边树桩连结拉紧，再在中央系一根绳，横向一拉，车就向前移动一些，再将钢索收紧再拉，如此反复，货车居然被一两个人拉出了泥洼。

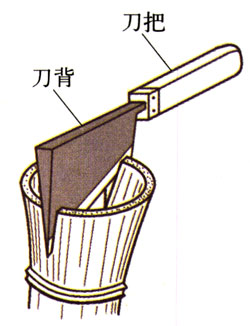
图2-26中一把刀正在劈开物体，刀非常锋利，成语中常用“迎刃而解”“锐不可当”“快刀斩乱麻”等来形容刀的锋利。刀之所以锋利在于它的刃部，刀刃在物理中常称为“劈”，它的截面是一个夹角很小的锐角三角形。

前面我们已经知道，几个力可以用一个力替代，叫做力的合成。反过来一个力也可以用几个力来替代，替代前后的效果相同，叫做力的分解。图2-25和图2-26中的两种现象都可以用力的分解方法来分析说明。

如果知道了杨浦大桥桥面的重力是G，若使桥面保持平衡的向上拉力为F，则F＝G。现在要求每根钢绳对桥面的力是多少？也就是用几个力来替代一个力（图2-27），替代这一个力的那几个力叫分力。

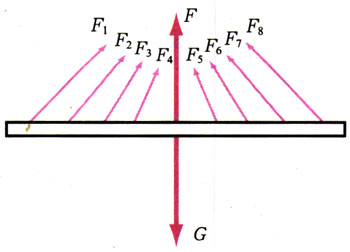
1．力的分解（resolution of force）

把一个力分解成几个分力的方法叫做力的分解。力的分解也是一种等效替代。

大家谈

一个力可以分解为多少个力？

理论上讲，一个力可以由任意个分力来替代。杨浦大桥上，拉住桥面的力是由100多根钢索产生的分力来承担的。

下面我们仅讨论一个力分解成两个力的简单情况。

力的分解遵循什么规则？

由逻辑推理可知，力的分解所遵循的规则也是平行四边形定则。

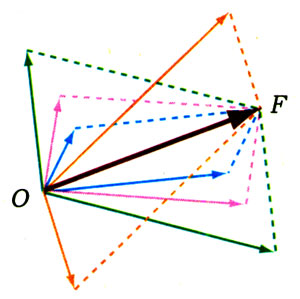
由图2-28可知，与OF相关的平行四边形也是无限多的。所以一个力分解为两个力也有无数组解，但是从解决实际问题的需要来看，其解也是可确定的。

2．一个力分解为两个共点力的方法

力的分解是力的合成的逆运算，同样可运用平行四边形定则。

在实际问题中怎样分解力呢？

让我们通过实例来说明找分力的方法。首先我们来讨论刀的“迎刃而解”的问题。

3．力的分解实例

（1）劈的分解

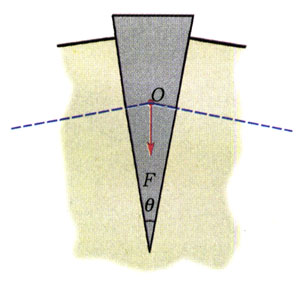
示例1    如图2-29所示是刀刃的横截面，F是作用在刀背上的力，它推开物体的两个力的方向是否明确？怎样用作图方法画出这两个分力？

分析：刀刃对侧面有挤压作用，所以分力一定垂直于刀刃的表面。

解答：运用平行四边形定则作图可求出分力，如图2-30所示。

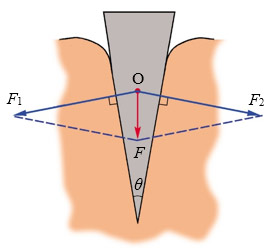
通过作图可看出“劈”的夹角越小，在一定大小的力F作用下，对物体的侧向推力F₁和F₂越大。

拓展联想

用计算方法求分力

若劈的夹角为θ，作用在刀臂上的力为F，如何求出分力F₁和F₂的大小？

试证明：

$$F_1=F_2=\frac{F}{2\sin \frac{\theta }{2}}$$

若θ＝10°，F＝10N，则可计算出侧向推力的大小为57.5N。

（2）斜面上物体所受重力的分解。

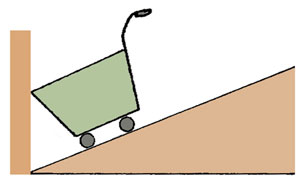
示例2    如图2-31所示，购物小车在斜坡上，它受到的重力应怎样分解呢？

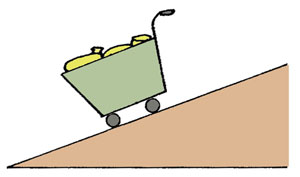
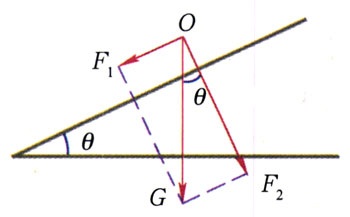
分析：小车沿斜面有下滑趋势，对斜面有垂直于斜面向下压的作用。因此，小车的重力可分解为这两个方向的分力。

解答：如图2-32所示，重力G分解为沿斜面产生下滑趋势的分力F₁和垂直斜面产生下压作用的分力F₂，则有

F₁＝Gsinθ，

F₂＝Gcosθ，

G＝$\sqrt{F_1^2+F_2^2}$。

想一想：如果θ角增大，两个分力的大小将如何变化？

DIS实验

用DIS验证斜面上力的分解

开启电源，运行DIS应用软件，点击实验条目中的“力的分解”。

实验时将重物放在倾角可变的斜面上，如图2-33所示，A、B为两个力传感器，软件界面上分别显示两分力的大小，如图2-34所示。改变斜面倾角，在表中记录不同倾角θ时的分力F₁、F₂。

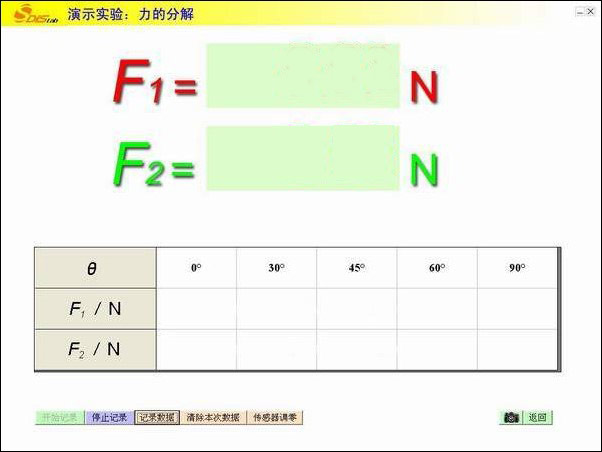
由上述测量结果分析：θ增加时，F₁、F₂如何变化？测量结果与用平行四边形定则分解的结果是否相同？

根据以上实例可知，一个力分解为两个力时，通常根据这个力产生的效果来确定分力的方向。

从上面两个实例中可以看出，当一个力分解为两个力时，通常都是根据力产生的实际效果来确定分力的方向。一种是产生形变的效果，如推、拉、提、压等；另一种是使物体运动状态变化或有变化趋势，如有加速度或运动趋势等。

一个物体在受几个力作用时，常采用建立直角坐标系方法，将每一个力分解为相互垂直的两个分力，以便于解决问题，这种分解方法后面还将进一步运用。

自主活动

1．图2-35中，小车靠着墙，计算它对墙与斜面的压力时，应怎样分解小车的重力？试画出力的分解图。（摩擦不计）

2．若斜面倾角为30°，小车重10N，则垂直于墙壁的分力为____，垂直于斜面的分力为____。

STS

1．赵州桥

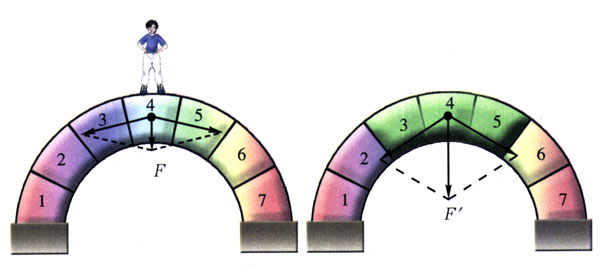
拱形结构是古代能工巧匠们的杰作。我国古代的赵州桥（图2-36）就是典型的代表作。它横跨浚河，长达37.37 m，是单孔石桥，建于隋代大业年间，距今已有1400年，比欧洲同类桥早了1200多年，展现了我国古代人民的智慧和高超的技术。拱桥是由许多楔形砖块砌成的，为什么拱形结构能承受很大压力呢？从图2-37所示的简化图中可以看出，站在桥中央的人和砖块“4”的合力F竖直向下，可以分解为对砖块“3”和“5”挤压的两个分力，人和砖块“3、4、5”看成整体又可将力分解到砖块“2、6”，以此类推，最终全部重力都分解到对桥墩的压力。所以，拱桥能承受很大的压力而不塌垮。

2．汽车千斤顶

图2-38中OABC是一个支架，称为举重器，俗称“千斤顶”。当汽车需要换轮胎时，司机将它放在车身底盘与地面之间，只需摇动手柄使螺杆OA转动，OA距离会渐渐减小，OC距离就会增大，将汽车车身缓缓地顶升起来。这是一个非常省力的机械，只需较小的力就能将汽车顶起，故名“千斤顶”。

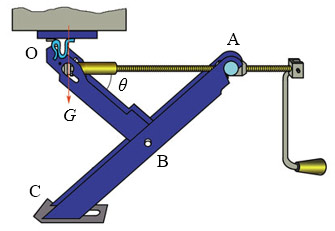
怎样求千斤顶升起来后OA杆所受的力呢？这就涉及作用在O点的压力怎样分解的问题。你不妨先做个试验体会一下：用拇指、食指捏住圆规的一个针脚，另一个有铅笔芯的脚支撑在手掌心位置，使OA水平，相当于千斤顶的螺杆，然后在圆规顶部挂上一些不太重的物品，如钥匙等，如图2-39所示。体会一下，A处和B处各受怎样的作用？

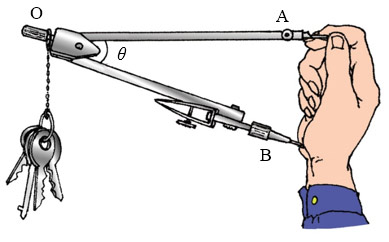
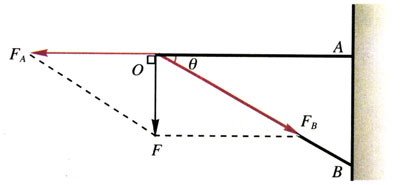
图2-40是力的分解图，钥匙对圆规的拉力F（大小等于G），可分解为沿OB方向的压力F_B和沿AO方向的拉力F_A。这样你就能求出两个分力的大小了。

发布时间：2015/9/18 下午10:19:10  阅读次数：1927