六、自由落体运动

跳伞运动员离开直升飞机后，在延迟开伞的十几秒里是竖直下落的；手里拿着的物体一松手就会竖直落向地面；用绳子挂在墙上的镜框，绳子断了，镜框就会竖直掉落下来。在地面附近的任何物体，脱离支持物后就会竖直落向地面，这种运动是一种常见的直线运动。

关于落体快慢的争论

当人们看到一个苹果比一片叶子下落得快时，似乎可以自然地得出“物体越重，下落越快”的结论（图3-35）。早在公元前4世纪希腊哲学家亚里士多德就曾断言：“物体的重量（这里所说的重量是指物体所受重力的大小）决定它们下落的快慢”。在以后的2000多年时间里，人们对这一论断一直深信不疑。

17世纪意大利物理学家伽利略（1564—1642）向这一“天经地义”的论断提出了挑战，在他的名著《两种新科学的对话》中，伽利略首先巧妙地揭露了亚里士多德论断的自相矛盾之处，并推断重物不会比轻物下落得更快些，他把物体下落快慢不同的原因，正确地归于空气阻力影响程度的不同。

现在我们用实验来研究，取两张大小相同的纸，将其中一张纸揉成团，另一张提着它的一端让它下垂着，在同样高处同时放手，观察它们是否同时落到地面？接着，再做一次实验，将另一张纸平放在手掌上，和纸团在同样高处同时释放，看它们是否同时落到地面？结果都是否定的，而且第二次实验中平放的纸下落更慢。

我们继续做实验，在同样高处同时释放揉成团的半张纸和平放的整张纸，观察结果表明还是纸团先落到地面。这表明物体在空气中下落的快慢，不但跟它们所受重力的大小有关，而且还跟它们受到的空气阻力的大小有关。纸张平着下落时受到的空气阻力，远大于纸团下落时受到的空气阻力。

我们日常见到的落体运动，是在物体既受到重力又受到空气阻力的情况下发生的。在科学研究中，懂得忽略什么跟懂得考虑什么是同样重要的。为使问题简化，伽利略假定不存在空气阻力，把物体只在重力作用下由静止下落的运动，叫做自由落体运动。

事实上，自由落体运动只有在真空条件下才能发生，但在处理实际问题时，如果下落物体所受的空气阻力比它所受重力小得多，空气阻力便可忽略不计，例如石块从不太高处由静止下落的运动，就可以看成是自由落体运动。

伽利略推断：轻重不同的物体从同一高度处自由下落，它们应同时落地，就是说不同物体作自由落体运动时，它们的运动情况是相同的。

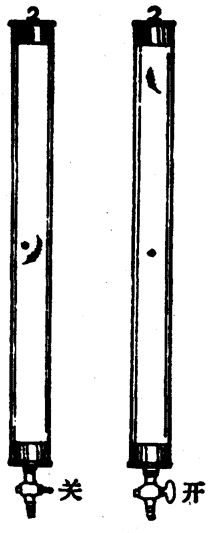
我们可以用实验来验证伽利略的推断。在抽成真空的玻璃管中，一片羽毛和一片金属的下落情况是完全相同的（图3-36）。打开开关后，空气进入玻璃管，羽毛的下落就明显慢于金属片。月球表面没有空气，宇航员登月时在月球表面进行了许多各种各样的科学实验（课本彩图8），其中就包括把铁锤和羽毛在同一高度同时释放的实验，结果它们同时落到月面。

伽利略对落体运动性质的研究

自由落体运动显然是一种加速直线运动。伽利略并没有像当时的哲学家那样，首先去争论使物体加速的原因，他抛弃了研究自然现象时首先寻找原因的古老方式，他认为还没有正确得出这种加速运动的规律，就去追究加速的原因为时尚早。伽利略分以下三步研究落体运动：

一、提出假设

伽利略认为落体运动是一种最简单的变速运动，并假设落体的速度随着时间均匀增大，即经过相等的时间Δt，落体速度的增加量Δv相等，落体的加速度a＝\(\frac{{\Delta v}}{{\Delta t}}\)是一个常量，他把这种运动叫做匀变速运动。也就是说伽利略假设落体运动是一种匀变速运动。

二、数学推理

在伽利略的年代，要测定很短的时间和瞬时速度，在技术上是不可能做到的，因此无法直接用实验方法验证落体的加速度是常量。于是伽利略用数学方法推导出物体从静止开始下落所经过的距离s跟时间t的关系。

设落体在t秒内下落的距离为s，在这段时间里落体运动的平均速度\(\bar v\)＝\(\frac{s}{t}\)。根据数学知识，任何一个均匀变化的量，它的平均值等于初值和终值的中间值，也就是初值与终值之和的一半，即\(\bar v\)＝\(\frac{{{v_0} + {v_t}}}{2}\)。对落体来说，v₀＝0，所以平均速度\(\bar v\)＝\(\frac{{{v_t}}}{2}\)，它的加速度a＝\(\frac{{{v_t} - {v_0}}}{a}\)＝\(\frac{{{v_t}}}{t}\)，于是v_t＝at，代入s＝\(\bar v\)t，得

s＝\(\bar v\)t＝\(\frac{{{v_t}}}{2}\)·t＝\(\frac{{at}}{2}\)·t＝\(\frac{{1}}{2}\)at²。

因此，只要验证落体的s∝t²（即\(\frac{s}{{{t^2}}} = \frac{a}{2}\)是个常量），便可证实所提出的假设。

三、斜面实验

由于在实验室中，一般落体的下落时间太短，要用实验证实自由落体的s∝t²，在当时仍难以做到。于是伽利略改用间接验证的方法。他在阻力很小的斜面上做了上百次实验，因为小球在斜面上运动的加速度要比它竖直下落时的加速度小得多，所以时间就容易测量。

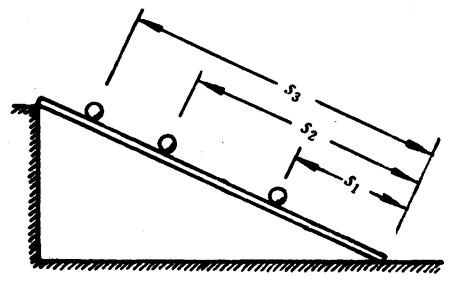
实验结果表明，从同一倾角的光滑斜面上的不同位置滚下的小球，它经过的距离s跟所用的时间t的平方的比是不变的，即s₁/t₁²＝s₂/t₂²＝s₃/t₃²（图3-37），从而证明了小球沿斜面的运动是匀变速直线运动。他又换用质量不同的小球重复实验，发现s/t²的比值仍不变，这表明不同小球沿同一倾角的光滑斜面做匀变速直线运动的情况是相同的。

随后，他把斜面的倾角增大，重复上面的实验，发现不同质量小球的s/t²的比值仍都相同，但这一比值比斜面倾角较小时的大，这说明不同质量的小球仍以相同加速度做一样的匀变速直线运动，但加速度已随斜面倾角的增大而变大。

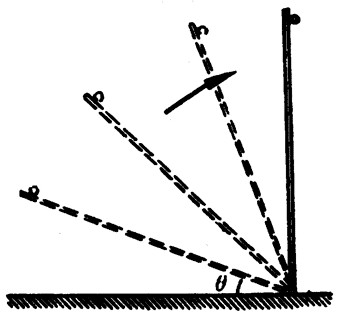
伽利略不断增大斜面倾角取得相同的实验结论，并把它合理外推，设想斜面倾角增大到90°（图3-38）时，不同质量的小球就都将竖直下落，只受重力作用，做自由落体运动，它们应该都做匀加速直线运动，它们的加速度是相同的，有一定的值。

伽利略对自由落体的研究，不但证明了自由落体运动是一种匀变速直线运动，也开创了研究自然规律的科学方法，这就是提出假设、数学推理和实验验证。伽利略是物理学发展中开辟道路的先驱者。

自由落体的加速度

今天距离伽利略时代已有3个世纪，当时无法用实验直接验证的结论，现在已完全可以用实验来证实，并精确地测出了自由落体加速度的值。因为做自由落体运动的物体只受重力作用，所以自由落体加速度也叫作重力加速度，用g表示。重力加速度的方向是竖直向下的。

理论研究和实验证明，地球表面各处的重力加速度g的大小不一样，它和该处的纬度和高度等有关，一般说来纬度越大，g值越大，高度越大，g值越小，而和物体本身质量的大小无关。在一般计算中，常把g值看成是已知量，取作9.8米/秒²。

思考

下面这条社会新闻，报导了一位青年工人接住一个从四楼窗口跌出的男孩的动人事迹。如果这个男孩直接从四楼窗口坠下，未碰到三楼的两根电线，而青工在接触男孩之前，男孩已下落10米，这位青工跳下自行车冲到窗下需1.2秒，若他能接住孩子，则至多允许有多长的反应时间？

六岁小男孩跌出四楼窗口

青工朱云华千钧一发及时接住

本报讯  日前，上钢五厂二炼钢分厂青工朱云华在千钧一发之际，勇救坠楼六龄童，被传为美谈。

3月19日下午1点30分，小朱骑自行车途经桃园新村15号时，突闻四楼朝西窗口传出呼叫“爸爸”、“爸爸”，小朱抬头一看，大惊失色，只见一个小男孩从四楼的窗户口坠落到三楼的两根220伏电线上，小朱毫不犹豫地跳下自行车，冲上前用双手去接，瞬间，男孩在电线上弹了几下又一直朝楼底坠落，在小朱的双手碰触缓冲下落到地面。小男孩脸色苍白，双眼直翻已经没有了声息。

小朱抱起男孩拦车，直驶吴淞中心医院。经医生急救，男孩恢复了神智。小男孩双目失明的父亲在邻居搀扶下赶到了。他拉着小朱的手说：“谢谢你，如果孩子活不成，我们全家都无法活了。你救了我们全家。”

小朱淡淡地说：“没什么，应该的。”随即掏出100元钱：“这钱你先付医药费，我去上中班。”

练习十五

1．试分析图3-39所示的小球自由下落时的频闪照片，已知频闪周期为0.04秒，直尺上的刻度单位是厘米。

（1）证明自由落体运动是匀变速运动；

（2）求出重力加速度的平均值（提示：用匀变速直线运动规律么Δs＝at²进行计算）。

2．自由落体运动是初速度等于零、加速度为g的匀变速直线运动，试写出自由落体下落距离h和下落速度v_t的计算公式。

3．上海东方明珠电视塔包括天线在内总高度为468米，如果有一物体从天线的最高处自由落下，求这个物体落到地面的时间。

4．有一重物从16层高的大楼顶端自由下落，经过最后7层的时间是0.8秒，求大楼的高度。

阅读材料    伽利略对落体运动的思考与研究

伽利略（Galileo Galilei，1564-1642）是意大利物理学家、天文学家、数学家，近代实验科学的创始人（图3-40）。他建立在科学的方法论基础之上的一系列科学活动，使他在物理学和天文学领域的许多方面有了一系列重大的发现、发明和创造。

1604年，他在比萨大学任教时，从理论上论证了落体运动的规律。伽利略对亚里士多德（Aristotle     古希腊哲学家、学者，B．C．384—322）认为重物比轻物下落要快的传统说法提出了疑问，伽利略在1638年出版的《关于力学以及地上运动的两个新学科中的对话和数学证明》巨著中指出：

按照亚里士多德的观点，如果把两个自然速率不同的物体连在一起，那么落得快的物体被落得慢的物体拖着而减速，慢的物体会被快的物体拉着而加速。但是，如果这是对的，那么我们取一块大石头，假定它的下落速率为8；再取一块小石头，下落速率为4，将它们拴在一起，整个系统的下落速率应该小于8；但是，两块石头拴在一起，下落速率应该比那块速率是8的石头还要大。这样，从重物比轻物下落得快的假设却推出了重物比轻物下落得更慢的自相矛盾的结论。

伽利略用简单明了的科学推理，巧妙地揭示了亚里士多德关于落体运动学说的矛盾，他还做了大量的实验研究落体运动的规律。伽利略认识到，在当时的技术条件下，不可能精确测定落体运动的加速度。他设法用小球在斜面上的运动来代替自由落体，将时间“放大”。他指出：如果自由落体的加速度是常量，那么一个小球在光滑的斜面上滚下，它的加速度虽然小一些，但也应该是常量。伽利略在《力学对话》中指出：

“用一块木料制成长约12库比特（库比特是一种古代的长度单位，1库比特等于0.4572米），宽半库比特，厚三指的板条，在它的上面刻一条比一指略宽的槽，将这个槽做得很直，打磨得很光滑，在槽上裱一层羊皮纸（也要尽可能光滑），取一个坚硬、光滑并且很圆的铜球，放在槽中滚动。将这个木槽的一端抬高1～2库比特，使槽倾斜。就像我要讲的那样把球放在槽顶让它沿着槽滚下，记录下降的时间。实验要重复几次，以便使测得的对间准确到两次测定的结果相差不超过一次脉搏的十分之一。进行这样的操作，肯定了我们的观察是可靠的以后，将球滚下的距离改为槽长的四分之一，测定滚下的时间，我们发现它准确地等于前者的一半。下一步，我们用另一些距离进行试验，把全长所用的时间与全长的二分之一、三分之二、四分之三，或者其他任何分数所用的时间相比较。像这样的实验，我们重复了整整100次，结果总是经过的距离与时间的平方成比例，并且在各种不同坡度下进行实验，结果也都如此……。”

在这样的实验基础上，伽利略得出推论，当斜面倾角增大到90°，小球做自由落体运动时，仍然是做匀加速运动。这一推论后来得到了实验证实。

本章学习要求

1．知道时间和时刻的区别。

2．知道打点计时器的功用，会从打点计时器的纸带和频闪照片计算研究对象运动的时间。

3．知道质点。

4．理解位移和路程的区别。知道矢量和标量。

5．理解匀速直线运动。

6．理解速度的概念。知道速度和速率的区别。

7．理解平均速度的概念。

8．知道瞬时速度。

9．知道匀速直线运动的速度图象和位移图象。

10．理解匀变速直线运动。

11．理解匀变速直线运动的加速度的概念。

12．知道匀变速直线运动的速度图象。

13．掌握匀变速直线运动的规律。

14．学会用打点计时器测定匀变速直线运动的加速度。

15．知道伽利略对落体运动的研究方法。

16．理解自由落体运动是初速度等于零的匀变速直线运动。

17．知道重力加速度及其方向。记住重力加速度的值。

复习题

1．列车从车站驶出做匀变速直线运动，在10秒内的位移为15米，求列车在第1秒内和第10秒的位移大小。

2．一辆自行车以5米/秒的初速度，驶入一段下坡道，加速度是0.4米/秒²，坡道长30米，试求自行车到达坡底时的速度和经过这段坡道所用的时间。

3．摩托艇通过拉索拉着滑水运动员在水上滑行（图3-41），摩托艇的速度为12米/秒。如果运动员突然松手放开拉索后还能向前运动4.5米，试求运动员在这一匀减速运动中的加速度以及运动的时间。

4．在图3-42中，哪一个速度图象最能描述上题中运动员的运动？

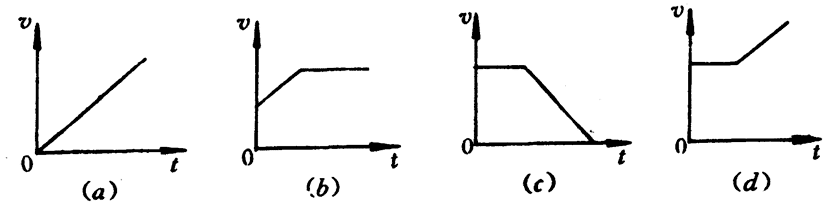
5．如图3-43所示，一辆实验小车由静止开始，从长度为1.5米的斜面顶端滑下，2秒末到达斜面底端。接着以到达斜面底端时的速度为初速，在一个水平的粗糙桌面上运动3秒钟停下。如果把小车在斜面上和水平桌面上的运动都看成是匀变速直线运动，试求

（1）小车在斜面上和水平桌面上运动时的加速度；

（2）小车在水平桌面上的运动距离。

6．进行测量工作的直升飞机，悬停在离地面80米的高处，放下一个标记，这个标记的下落可看成是自由落体运动。这个标记在最后1秒钟里，下降了多少高度？（本题计算中，g取10米/秒²）

7．宇航员在月球表面做落体实验，从离月球表面1.5米高处由静止释放一小球，测得下落时间为1.36秒，试求月球表面的自由落体加速度。

8．居住在高层住宅底楼的居民，看到窗外有一个衣架贴近窗框落下。已知窗框的长为1.8米，估计衣架经过整个窗框的时间为0.1秒。若把衣架的下落看成是自由落体运动，那么这个衣架是从几楼掉下的？（设每层楼高3米，g取9.8米/秒²）

9．图3-44所示的是利用打点计时器记录的一个重锤自由下落时的一段纸带，已知纸带上左端的第一个点是开始运动的点，每两个点间的时间间隔T＝0.02秒，试在纸带上选择并标出记数点，用毫米刻度尺量出右关数据，且填写在你自己设计的表格中，要求：

（1）判断重锤的下落运动是否是匀变速直线运动；

（2）测出重锤下落运动中的加速度。

发布时间：2015/9/12 下午9:57:38  阅读次数：4016