五、匀变速直线运动的速度和位移

变速直线运动的速度

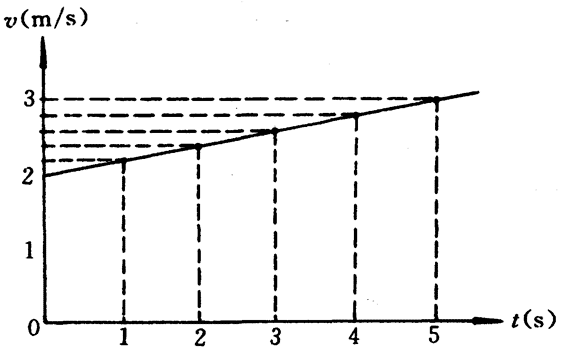
从车站开出的列车在一段时间内的运动可以看成是匀变速直线运动，如果知道在5秒钟里列车速度由2米/秒增大到3米/秒，在这5秒钟内速度的增加情况如下表所列：

根据这些数据可以描绘出在这5秒内列车运动的速度图象，如图3-30所示。可以看出它是一条不通过坐标轴原点的一倾斜直线，表明了匀变速直线运动的瞬时速度是时间的一次函数。从图象可以求出列车运动时任何时刻的速度。

我们也可以根据匀变速直线运动的加速度定义式a＝\(\frac{{{v_t} - {v_0}}}{t}\)，推导得出做匀变速直线运动的物体在t秒末的瞬时速度公式

v_t＝v₀＋at。

公式中加速度a和初速度v₀都是不变的量，表明t秒末的瞬时速度v_t是时间t的一次函数。

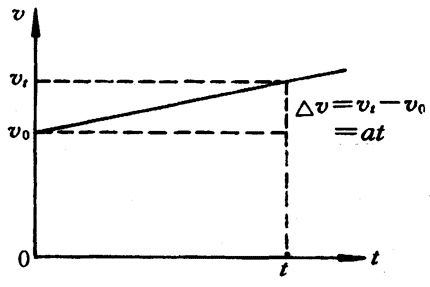
从速度公式还可以看出，做匀变速直线运动的物体在t秒末的速度等于初速度v₀与at两部分的和，因为v₀是不变的，所以引起速度变化的是含有时间变量t的at部分，也就是说速度的变化Δv＝v_t－v₀＝at，这在速度图线上也能明显地看出（图3-31）。从图线还能看出，图线在秒轴上的截距就等于初速度v₀，而图线的斜率\(\frac{{\Delta v}}{{\Delta t}}\)就表示加速度。

【例题】

原以5米/秒的速度匀速行驶的汽车，以2米/秒²的加速度加速行驶5秒钟，则速度变为多大？速度变化多大？

解：根据匀变速直线运动的速度公式，汽车加速行驶5秒末的瞬时速度

v_t＝v₀＋at＝（5＋2×5）米/秒＝15米/秒。

速度变化       Δv＝v_t－v₀＝at＝2×5米/秒＝10米/秒。

思考

1．怎样用公式表示初速度等于零的匀变速直线运动的瞬时速度随时间而变化的规律？

2．以某一速度行驶的列车准备靠站，速度逐渐均匀变小直到停止运动，在这段时间里的速度-时间图象应是怎样的？

3．若把两个初速度等于零、加速度不等的匀变速直线运动的速度-时间图线，按同一标度画在同一个直角坐标系中，其中加速度较大的一条v-t图线比较靠近v轴还是比较靠近t轴？

练习十二

1．长征2号火箭点火后开始升空，3秒末的速度达到38米/秒，试求火箭3秒内的加速度。

2．以10米/秒行驶的汽车，制动时的加速度是－4米/秒²，需要经过几秒钟汽车才能停下？

3．速度是72千米/时的列车，以0.4米/秒²的加速度加速行驶了12.5秒，这时的速将达到多少千米/时？

4．滑雪运动员以某一速度滑下雪坡，已知下滑时的加速度为2米/秒²，下滑6杪钟到达坡底时的速度达到15米/秒，试求这位运动员在开始下滑时的初速度。

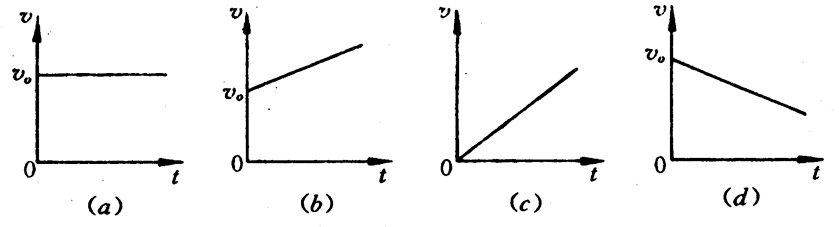
5．你能区别以下几个速度图象（图3-32）所描述的分别是什么运动吗？

匀变速直线运动的位移

匀速直线运动的速度图线与时间轴间包围的面积，在数值上等于物体的位移。这个结论同样适用于匀变速直线运动。

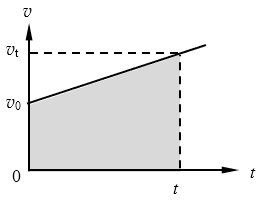
图3-33所示的是某个匀变速直线运动的速度图象，在图线以下用阴影表示的一块梯形面积，在数值上应等于做匀变速直线运动的物体在t秒内的位移，即

s＝\(\frac{1}{2}\)（v₀＋v_t）t＝\(\frac{1}{2}\)（v₀＋v₀＋at）t＝v₀t＋\(\frac{1}{2}\)at²。

于是得出做匀变速直线运动的物体，在t秒内的位移公式

s＝v₀t＋\(\frac{1}{2}\)at²。

公式表明做匀变速直线运动的物体的位移是时间的二次函数。

【例题1】

原来以10米/秒的速度行驶的列车，经25秒钟速度均匀增大到20米/秒。求在这段时间里列车的位移。

解：根据题意可先求出列车运动的加速度

a＝\(\frac{{{v_t} - {v_0}}}{t}\)＝\(\frac{{20 - 10}}{{25}}\)米/秒²＝0.4米/秒²

于是列车在这段时间里的位移

s＝v₀t＋\(\frac{1}{2}\)at²＝10×25＋0.5×0.4×（25）²米＝375米。

【例题2】

以5米/秒的速度行驶的自行车，驶至交叉路口离停车线约3～4米远处忽见红灯信号，骑车人赶紧刹车制动，经2秒钟车才停下。如果自行车刹车后的运动可看成匀减速直线运动，这个骑车人是否会超越停车线？

解：自行车的加速度

a＝\(\frac{{{v_t} - {v_0}}}{t}\)＝\(\frac{{0 - 5}}{{2}}\)米/秒²＝－2.5米/秒²

在这段时间里自行车继续向前运动的距离为

s＝v₀t＋\(\frac{1}{2}\)at²＝5×2＋0.5×（－2.5）×（2）²米＝5米。

可见这位骑车人虽已刹车，但车停下时已经超越了停车线，这是违反交通规则的。所以任何车辆在驶近交叉路口时，必须控制车速不要太大，不然是不安全的。

我们已经知道做变速直线造动的物体在时间t里的位移s可以用平均速度\(\bar v\)计算，即s＝\(\bar v\)t，而s＝\(\frac{1}{2}\)（v₀＋v_t）t，

于是       \(\bar v\)t ＝\(\frac{1}{2}\)（v₀＋v_t）t，

消去t，得     \(\bar v\)＝\(\frac{{{v_0} + {v_t}}}{2}\)。

可见，匀变速直线运动中的平均速度等于初速度和末速度之和的一半。

思考

1．能否利用平均速度的概念来求解例题1？试试看。

2．初速度等于零的匀变速直线运动的位移公式应是怎样的？你能把它写出来吗？

练习十三

1．民航客机沿起飞跑道开始滑行，以4米/秒的加速度滑行40秒后脱离跑道升空，试求客机在跑道上滑行的距离。

2．以25米/秒的速度行驶的列车，紧急制动后，经10秒钟停下。试求在制动过程中列车的位移。

3．在平直道路上行驶的速度为20米/秒的汽车，以－5米/秒²的加速度制动，试求5秒内汽车的位移。

4．根据初速度等于零的匀变速直线运动的位移s跟时间t的平方成正比，试证明在各连续相等的时间里的位移（图3-34）的比s_Ⅰ∶s_Ⅱ∶s_Ⅲ∶……＝1∶3∶5∶……。

5．地铁列车从车站开出做匀加速直线运动，2秒内的位移是2.4米，求6秒内的位移。

匀变速直线运动的速度和位移的关系

列车自车站驶出，做匀变速直线运动，随着位移的增大，它的速度也逐渐增大起来。那么，匀变速直线运动速度和位移有怎样的关系呢？让我们从匀变速直线运动的速度公式和位移公式中，消去时间变量t来进行研究。

根据匀变速直线运动的速度公式v_t＝v₀＋at，得

t＝\(\frac{{{v_t} - {v_0}}}{a}\)

代入匀变速直线运动的位移公式

s＝v₀t＋\(\frac{1}{2}\)at²＝v₀（\(\frac{{{v_t} - {v_0}}}{a}\)）＋\(\frac{1}{2}\)a（\(\frac{{{v_t} - {v_0}}}{a}\)）²＝\(\frac{{v_t^2 - v_0^2}}{{2a}}\)，

整理后，得

v_t²－v₀²＝2as。

这是一个有用的推论，它表示了做匀变速直线运动的物体的速度跟位移之间的关系。

【例题1】

赛车起动后做匀变速直线运动，行驶了30米，速度达到90千米/时，试求赛车的加速度。

解：已知赛车的初速度v₀＝0，末速度v_t＝90千米/时＝25米/秒，位移s＝30米。

根据                  v_t²－v₀²＝2as，

赛车的加速度       a＝\(\frac{{v_t^2 - v_0^2}}{{2s}}\)＝\(\frac{{{{25}^2} - 0}}{{2 \times 30}}\)米/秒²＝10.4米/秒²。

【例题2】

汽车以8米/秒的速度行驶，因前方道路交通阻塞进行刹车，如果刹车时产生的加速度为－4米/秒²，刹车后汽车还能前进几米？

解（1）：根据匀变速直线运动的加速度a＝\(\frac{{{v_t} - {v_0}}}{t}\)，已知v₀＝8米/秒，a＝－4米/秒²，当汽车停止运动时v_t＝0。

经过的时间           t＝\(\frac{{{v_t} - {v_0}}}{a}\)＝\(\frac{{0 - 8}}{{ - 4}}\)秒＝2秒，

于是，s＝v₀t＋\(\frac{1}{2}\)at²＝8×2＋0.5×（－4）×（2）²米＝（16－8）米＝8米。

汽车刹车后还能前进8米。

解（2）：根据v_t²－v₀²＝2as，已知v₀＝8米/秒，v_t＝0，a＝－4米/秒²。刹车后汽车还能前进的距离

s＝\(\frac{{v_t^2 - v_0^2}}{{2a}}\)＝\(\frac{{0 - {8^2}}}{{2 \times ( - 4)}}\)米＝8米。

以上两种解法相比较，显然解（2）比较简捷。

在解直线运动的问题时，首先必须弄清题目所描述和研究的过程是什么性质的运动，明确题目要求解决的是什么问题，哪些量已经给出，哪些量可以间接知道。然后要在理解公式的物理意义和使用范围的基础上运用有关公式进行计算，切忌死套公式。解题时还应注意正确使用物理量的单位。

练习十四

1．已知一辆实验小车从斜面顶端自静止开始下滑，下滑时的加速度为2米/秒²，斜面长为1.2米，试求小车滑行到斜面底端时的速度。

2．一辆客车以1.5米/秒²的加速度加速行驶12米，它的速度达到36千米/时，试求客车加速前的速度。

3．公安部门规定上海市区交通繁忙路段，机动车辆的速度限制在25千米/时，并要求驾驶员必须保持大于5米的车距。如果考虑到汽车制动时的加速度可达－6米/秒²，试从匀变速直线运动规律分析制订这些规定的依据。

4．游客从喷水滑梯顶端由静止滑下，冲入池中时的速度可达4米/秒，已知滑梯长16米，求游客从滑梯滑下时的加速度和在滑梯上滑行的时间。

发布时间：2015/9/12 下午9:30:59  阅读次数：3150