四、匀变速直线运动 加速度

常见的直线运动中，有许多是变速运动。例如，列车从某个站驶出，列车的瞬时速度逐渐变大，做加速运动；列车行驶一段路程后准备停靠另一个站时，列车的速度就得逐渐变小，做减速运动。又如飞机起飞过程（本章导图3）也是变速运动。原先飞机停在起飞跑道上，速度等于零，接到起飞命令后，驾驶员立即起动飞机，由于跑道的长度是有限的，而飞机脱离跑道升空时又必须达到某个规定的较大速度，这就要求驾驶员在不太长的距离内，使飞机的速度很快增大。因此，在变速运动中还存在着速度变化快慢的问题，对于列车从车站驶出的运动来说，速度变化是比较慢的，而飞机起飞时，速度变化则要求很快。有些变速运动速度变化的快慢也是随时改变的。在各种变速运动中，速度变化最简单的是匀变速直线运动。

匀变速直线运动

喷水滑梯（图3-22）是一项新型娱乐设施，由于滑梯表面有一层自上而下流动着的水，人们从滑梯滑下时，摩擦阻力很小，下滑速度越来越大，是一种变速直线运动。现在我们通过实验来研究这种变速直线运动。

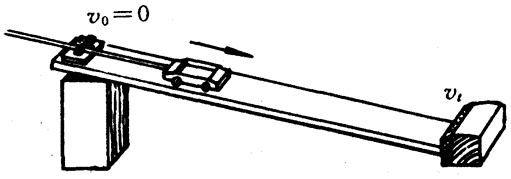
把一辆实验小车放在斜面顶端，由静止释放，让小车沿斜面向下运动，利用打点计时器记录小车的运动情况（图3-23）。小车到达斜面底端后，取下纸带，然后对纸带上记录的点子进行处理，以纸带开始运动的点为起点，记作0，以后每隔5个点作为一个记数点，按顺序编为1，2，3，4，5（图3-24所示是某次实验中所得的纸带）。然后把纸带从0，1，2，3……各记数点处剪开，并将各段纸带的下端沿一条基准线依次排列贴在一起（图3-25）。可以看出小车在连续相等时间里的位移逐渐增大。

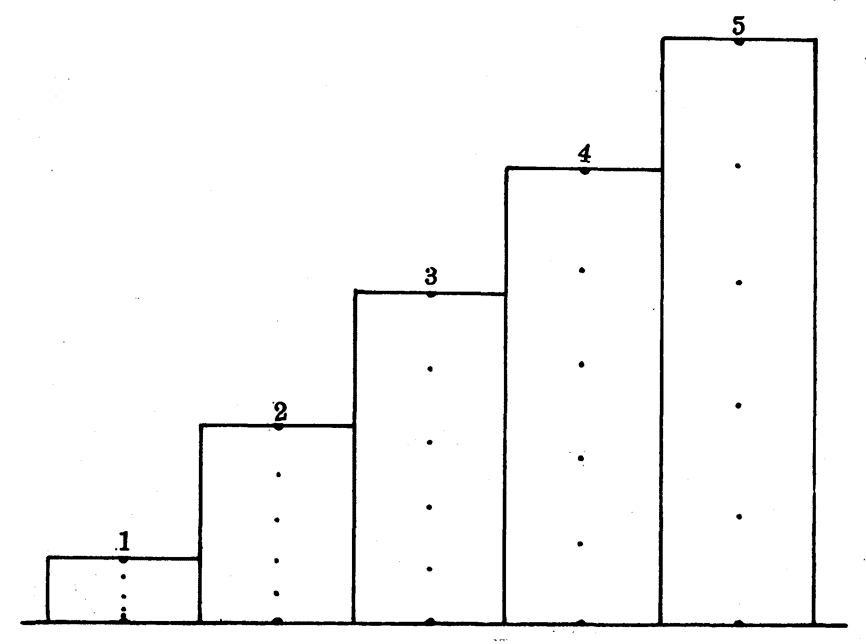
用刻度尺量得各段纸带的长度为s，根据各段时间间隔t（0.1秒），就能算出小车在各段连续相等时间里的平均速度\(\bar v\)。实验数据和计算结果如表一所示。

从上表可以进一步看出小车在连续相等时间里的位移差基本上是相等的，平均约为1.35厘米。在各段连续相等时间里的平均速度是逐渐增大的，它们的差也是基本相等的。

现在我们进一步分析记数点4—5的这段纸带的数据，量出这段纸带中每两点之间的距离，根据时间间隔为0.02秒，计算在这五段连续相等的时间里的平均速度。测量和计算结果如表二所示。

计算结果表明，在这五段连续相等时间里的平均速度也是逐渐增大的，并且每个0.02秒内的平均速度的增加量相等，而第1个和第2个0.02秒内的平均速度都小于记数点4—5的这段时间里的平均速度，第4个和第5个0.02秒内的平均速度又都大于记数点4—5的这段时间里的平均速度。这就给我们一个重要的启示：时间间隔取得越小，计算出的平均速度就越能反映做变速直线运动物体的实际运动速度。

如果取一直角坐标，以横轴表示时间，纵轴表示速度，将表一中的时间和相应的平均速度描绘出来，就得到如图3-26所示的v-t图象。将表二中的时间和相应的平均速度描绘出来，就得到如图3-27所示的图象。

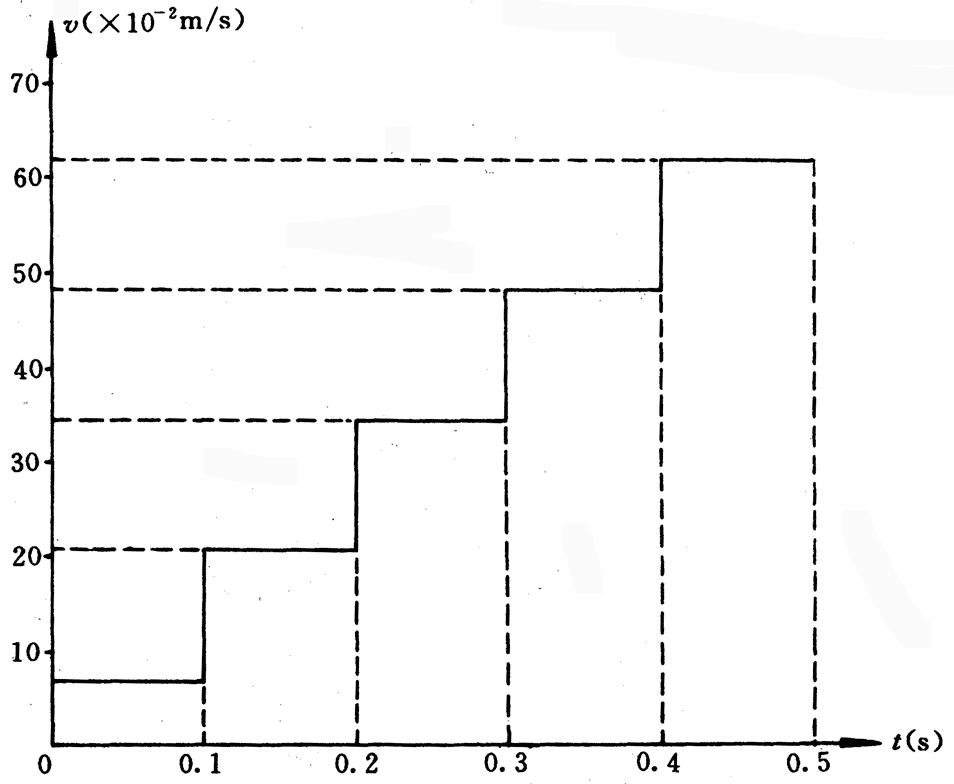
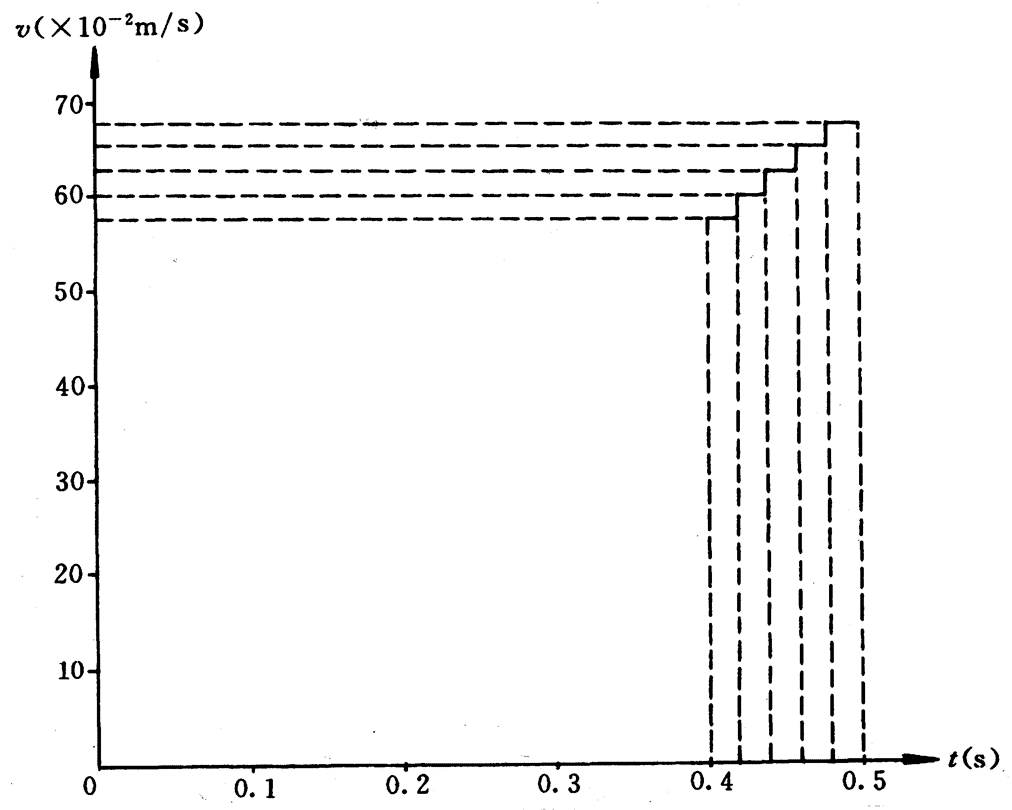
同样，依次将前面各单位时间内记录位移的各段纸带也作如上的处理，并将图3-26和图3-27加以比较，可以想象只要这些相等的时间间隔取得足够小，计算得出的一系列平均速度，就能看成是小车在各个时刻的瞬时速度，就可以用来绘出小车运动的速度图象，如图3-28所示。可以看出这是一条通过坐标轴原点的倾斜直线。这表明由静止开始运动的小车的瞬时速度v跟时间t成正比。也就是说每隔相等时间Δt，瞬时速度的增加量Δv是相等的。这表明了小车的瞬时速度随时间均匀变化的特点。

在相等时间内，速度变化量相等的直线运动，叫做匀变速直线运动。

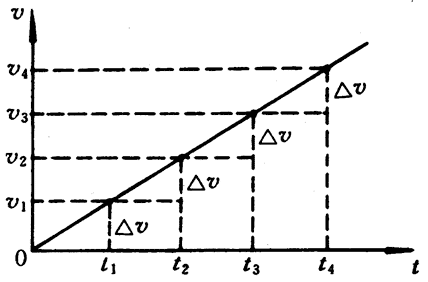
因此，不论物体是否从静止开始运动，也不论物体是加速还是减速，只要符合上述规律，物体就是做匀变速直线运动。实际生活中常见的许多变速直线运动并不完全符合上述规律，它们中有的是很接近匀变速直线运动。列车从车站开出、飞机在起飞跑道上开始滑行、人们从喷水滑梯上滑下的运动等等，都可以把它们看成是匀变速直线运动。

加速度

小轿车起动后，驾驶员踩下油门踏板（图3-29），轿车速度就会很快增大起来，而一辆公共汽车起动后，速度虽然也会增大起来，但是要用较长的时间。一颗子弹在枪膛里未被击发时速度等于零，一经击发，可以在极短时间内以数百米每秒的速度飞离枪口，而一架超音速喷气客机从开始起飞到达与子弹同样大小的速度，就要经过比较长的时间。上述事例表明在不同的变速直线运动中，速度变化的快慢是不同的。要比较物体运动速度变化的快慢程度，就需要比较在相同的时间内，物体速度变化的大小。

在匀变速直线运动中，物体的速度变化跟发生这一速度变化所用时间的比，叫做匀变速直线运动的加速度。

建立了加速度（acceleration）概念，就可以用加速度来描述物体速度变化的快慢，譬如上例中的小轿车的加速度比公共汽车的加速度大；子弹在枪筒里运动的加速度远大于超音速客机在起飞过程中的加速度。

如果用v₀表示开始时刻物体运动的速度（初速度），用v_t表示经过一段时间t后物体运动的速度（末速度），则在时间t内物体的速度变化为v_t－v₀，于是加速度a可用如下的定义式表示：

\[a = \frac{{{v_t} - {v_0}}}{t}\]

加速度单位是由速度单位和时间单位来确定的。速度单位是米/秒，时间单位是秒，则加速度的单位是米/秒²，读做“米每二次方秒”，符号是m/s²。

加速度不但有大小，而且有方向，加速度是矢量。

问题探讨

S：速度和加速度都是描述物体运动状态的量，它们有什么区别呢？

T：速度和加速度是两个完全不同的概念。速度是描述物体运动快慢的物理量；加速度是描述物体速度变化快慢的物理量。

在不同的匀速直线运动中，速度可以有不同的数值，但加速度都等于零。在匀变速直线运动中，加速度是不变的，而速度是时刻变化着的。

【例题1】

列车从车站由静止开始行驶，经1分钟速度达到12米/秒，若把列车的运动看成是匀变速直线运动，列车的加速度是多大？

解：已知列车的初速度v₀＝0，末速度v_t＝12米/秒，经过时间t＝1分＝60秒。

列车加速度    a＝\(\frac{{{v_t} - {v_0}}}{t}\)＝\(\frac{{12 - 0}}{60}\)米/秒²＝0.2米/秒²。

【例题2】

以30米/秒的速度行驶的列车，司机发现前方路段给出低速行驶的信号，于是采取制动措施，在10秒钟内使列车的速度减小到10米/秒，若把制动过程中列车的运动看成是匀变速直线运动，试求列车运动的加速度。

解：已知列车的初速度v₀＝30米/秒，末速度v_t＝10米/秒，经过时间t＝16秒。

列车加速度    a＝\(\frac{{{v_t} - {v_0}}}{t}\)＝\(\frac{{10 - 30}}{{10}}\)米/秒²＝－2米/秒²。

由以上两个例题可以知道匀变速直线运动有两种情况，一种是速度逐渐增大的匀加速直线运动，末速度大于初速度，v_t－v₀＞0，速度的变化量是正值，匀加速直线运动中的加速度是正值，表示加速度方向与物体运动的方向相同。另一种是速度逐渐减小的匀减速直线运动，末速度小于初速度，v_t－v₀＜0，速度的变化量是负值，匀减速直线运动中的加速度是负值，表示加速度方向与物体运动的方向相反。

做匀变速直线运动的物体，不论它的速度随着时间均匀增大，还是均匀减小，它的加速度的大小和方向都不随时间变化。

思考

1．发射“亚洲一号”卫星的“长征3号”（CZ-3）运载火箭，刚开始点火升空时的加速度可达14米/秒²，所以火箭开始升空时的速度就很大，这一说法对吗？为什么？

2．新设计的高速列车的最高时速可达354千米/时，它的加速度一定很大，这一说法对吗？为什么？

问题探讨

S：做匀变速直线运动的物体，加速度大，速度一定大吗？

T：做匀变速直线运动的物体，加速度是不变的，而速度v_t的大小，除决定于加速度a外，还决定于时间变量t以及物体是否具有初速度v₀；而且，匀变速直线运动还包括匀加速和匀减速两种情况。所以，加速度大，说明这时速度变化快，并不说明速度一定很大；加速度小，说明这时速度变化慢，也并不说明物体速度一定很小，要根据运动的具体情况才能确定速度的大小。

练习十一

1．用加速度概念可以描述（    ）

（A）物体运动的快慢；            （B）物体增加的速度；

（C）物体速度变化的大小；     （D）物体速度变化的快慢。

2．关于加速度概念的理解与应用，以下说法中正确的是（    ）

（A）加速度越大，物体的运动速度也越大；

（B）加速度很小，物体的运动速度不可能大；

（C）加速度等于零的运动是匀速直线运动；

（D）存在加速度的运动，速度总是增大的。

3．跳伞运动员在1200米高空从悬停在空中的直升飞机上跳下，在延迟开伞的2秒末，速度达到19.6米/秒。试求在这2秒内运动员下落运动中的加速度（运动员离开机舱的初速度看作零）。

4．原来以90千米/时的速度行驶的列车，紧急制动后经1分钟列车完全停止运动，试求列车在制动过程中的加速度。

发布时间：2015/9/12 下午9:02:42  阅读次数：1531