三、运动快慢的描述

匀速直线运动  变速直线运动

机械运动按运动轨迹来划分，有曲线运动和直线运动两大类。在直线运动中，运动的快慢，有的是不均匀的，有的是均匀的。例如城市道路上行驶的车辆，它的快慢通常是不均匀的。当车辆驶上平直的高速公路时，在一段距离内，车辆运动的快慢可以是均匀的。也就是说，在相等的时间里，车辆的位移都相等。

在相等的时间里，物体的位移都相等的直线运动，叫做匀速直线运动。匀速直线运动是一种最简单的机械运动。在相等的时间里，物体的位移不相等的直线运动则是变速直线运动。

速度

物体不论做匀速直线运动，还是做变速直线运动，不同物体运动的快慢程度往往是不同的。研究物体运动的快慢对交通运输，工农业生产和人们的日常生活都是很必要的。例如工厂流水线的传送带要按一定的快慢运行，才能保证各段工序的完成；铁路运输中控制列车运行的快慢，对在规定的时间能否走完预定的路程，具有十分重要的意义，列车的调度必须考虑列车运行的快慢，以保证行驶安全，提高铁路的运输效能。

日常生活中，我们说骑自行车比走路快，汽车比自行车快，飞机比汽车更快，根据是什么？比较物体运动快慢的根据是物体移动相同距离所用时间的多少，所用时间越少就越快；或者是物体在相等时间内所移动距离的长短，移动距离越长就越快。但是物体的运动并不都是在相同时间内或相等距离里进行的，所以必须建立速度（velocity）的概念。

速度等于物体的位移跟发生这段位移所用时间的比。

如果位移用s表示，时间用t表示，速度用v表示，就可以写成以下公式：

\[v = \frac{s}{t}\]

这一定义对于匀速直线运动和变速直线运动同样是适用的。所不同的是，在变速直线运动中由这一公式算出的是物体在某段位移中或某段时间里的平均速度。

速度是矢量

物体所作的机械运动有不同的方向。在研究和描述物体的运动时，只知道它的快慢是不够的，还必须了解运动的方向。天文学家能够准确预言1994年7月将发生苏梅克-列维9号彗星的碎片跟木星相撞的事件，是对彗星运行轨道和彗垦运动的快慢和方向都作了周密观测和精确计算的结果。通常我们所说的物体运动的方向，就是指速度的方向。速度不但有大小，还有方向，因此速度是矢量。

为了描述和计算的方便，通常规定速度的正方向跟位移的正方向相同。以民航班机的运动为例，如果以上海为始发站，北京为终点站，位移矢量是由上海指向北京，所以从上海飞往北京的班机速度取正方向，从北京飞回上海的班机速度取负方向；又如对于向上抛出的小球的运动来说，常以向上的位移为正方向，所以上升过程中小球的速度取正方向，小球回落时的速度取负方向。

今后，在讨论分析物体的运动时，如果说已知某物体的运动速度，就是指它的速度大小和方向都是确定的。速度的大小通常又叫做速率（speed），速率是标量。

匀速直线运动是速度大小和方向都不变的运动。

思考

1．你对速度的概念比初中有哪些进一步的理解？

2．机床操作中的“高速切削”、交通运输中的“高速列车”、“高速公路”，这里所说的“高速”指的是速度还是速率？

瞬时速度

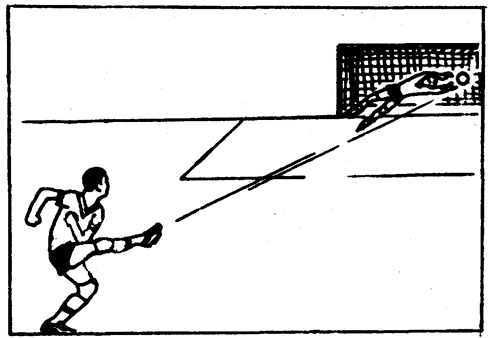
足球运动员劲射时，可使足球的速度超过100千米/时（图3-10），这个数字说明了什么？事实上足球不可能在1小时内飞出100千米远的距离，这仅表示足球在离开运动员脚的瞬间的运动员脚的瞬间的运动快慢。

运动物体在某一时刻的速度，或经过某一位置时的速度，叫做瞬时速度。

瞬时速度是矢量。建立了瞬时速度的概念，就能确切地描述做变速运动的物体在任一时刻或经过任一位置时的运动快慢和运动方向。

通常，人们往往把物体在包括某一时刻在内的极短时间里的平均速度，看成是物体在这一时刻的瞬时速度。时间取得越短，求出的平均速度就越接近于这一时刻的瞬时速度。

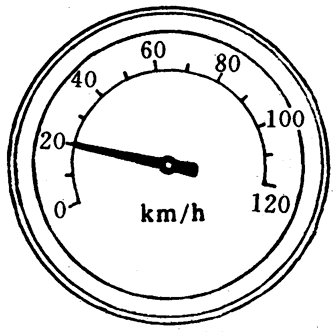
汽车驾驶台上的速度计是用来指示汽车行驶时瞬时速度大小的一种仪表（图3-11）。汽车在交叉路口等候绿灯信号时的瞬时速度等于零。当绿灯亮起，驾驶员立即发动汽车，经过2秒钟速度达到14.4千米/时。这是指汽车运动了2秒钟，在2秒末这一时刻的瞬时速度的大小是14.4千米/时（合4米/秒），但并不表示在过去的2秒内汽车已经行驶了8米，也不表示在以后的1秒钟内汽车的位移一定等于4米。

思考

1．手枪子弹从枪口飞出时速度可以达到500米/秒，这是指的什么速度？

2．运动员竖直向上托起一个排球，排球上升时速度逐渐减小，排球回落时速度逐渐增大，这都是指什么速度？在整个过程中，这个排球的速度有没有等于零的时刻？

3．对一个做匀速直线运动的物体来说，它的速度跟它在某段时间里的平均速度以及任一时刻的瞬时速度有怎样的关系？

练习十

1．杭州在上海西南约201千米处，直达列车于23时15分自上海开出，于次日2时45分抵达杭州，假定火车做直线运动，它的平均速度是多大？

2．两根路灯杆A、B相距40米，一辆汽车用3.2秒时间驶过这两根路灯杆（图3-12），根据这些数据可以计算出汽车在这段位移中的______速度＝_____米/秒。

如果灯杆A的近旁相距0.14米处有一块路牌，汽车驶过路牌和灯杆A间的这一小段距离只用了0.01秒，在这段时间里的平均速度＝____米/秒。可以认为汽车驶过灯杆时的_____速度＝______米/秒。

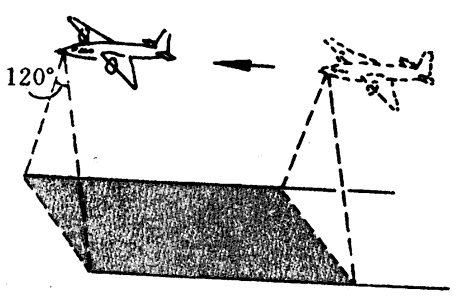
3．用飞机进行航空测量，飞机离地高度保持500米，巡航速率为540千米/时，飞机上的测量仪器可在120°的视角范围内测量（图3-13），飞机每小时测量的覆盖面积是多大？

匀速直线运动的速度图象

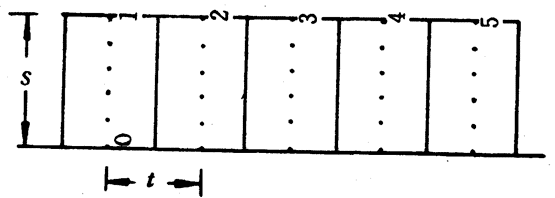
用打点计时器记录某个物体的运动时，如果纸带上每两个点间的距离是相等的，表明物体是做匀速直线运动。如果以每打5个点的时间为一个时间单位，即t＝5×0.02秒＝0.1秒，然后在纸带上从某个点开始每隔5个点进行编号，记作0，1，2，3，……（图3-14），把纸带从0，1，2，3，……各点处剪开，并将各段纸带的起点沿一条作为基准的直线依次并排贴在一起（图3-15）。可以看出1、2、3，……各点的连线是一条与基准线平行的直线。这表明物体在每个0.1秒时间内的位移是相等的，如果测得这段位移s＝2厘米，那么这个做匀速直线运动的物体的速度v＝\(\frac{s}{t}\)＝\(\frac{{2 \times {{10}^{ - 2}}}}{{0.1}}\)米/秒＝0.2米/秒。

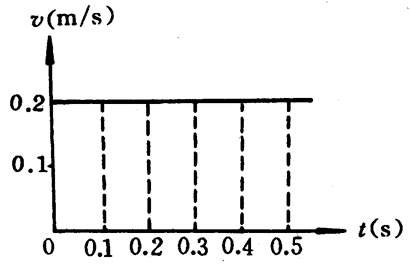
如果以速度为纵轴、时间为横轴建立一个直角坐标，把这一匀速直线运动的速度跟时间的关系用速度-时间图象（v-t图象，简称速度图象）来表示，它应是一条平行于时间轴的直线，这表明匀速直线运动的速度不随时间变化（图3-16）。

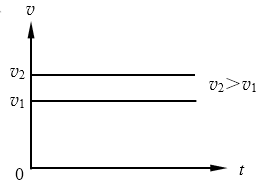
如果把两个速度不相等的匀速直线运动速度的图象，按同一标度描绘在一个直角坐标系中，就可形象地比较这两个匀速直线运动速度的大小（图3-17）。

匀速直线运动的位移图象

从匀速直线运动的速度公式v＝\(\frac{s}{t}\)，可以得到s＝vt，这就是匀速直线运动的位移公式。式中速度v是常量，所以匀速直线运动的位移s跟时间t成正比，位移是时间的一次函数。这一函数关系用图象来表示，就是匀速直线运动的位移-时间图象（s-t图象，简称位移图象）。

根据上述纸带记录的运动，可列出时间t与它对应的位移s的数据表：

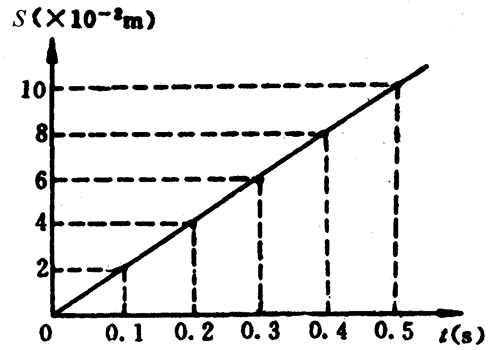
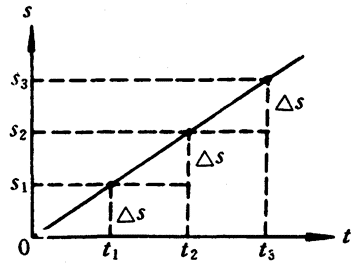
从实验数据，用描点法可以画出这一匀速直线运动的位移图象（图3-18）。由图象可以看出这是一条通过坐标轴原点的倾斜直线，表明了每隔相等时间Δt位移的增加量Δs是相等的。这正反映了匀速直线运动的位移s随时间t发生均匀变化的特点（图3-19）。

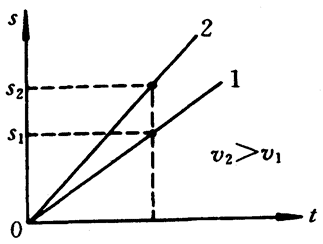
如果把两个速度不相等的匀速直线运动的位移图象，按同一标度画在同一个直角坐标系中，可以看出这两条倾斜直线的斜率是不等的，表明这两个运动在相等时间里的位移是不相等的，即\(\frac{{{s_2}}}{t}\)＞\(\frac{{{s_1}}}{t}\)，也就是v₂＞v₁。所以匀速直线运动的位移图线的斜率象可以表示速度的大小，位移图线的斜率越大，表示速度越大（图3-20）。

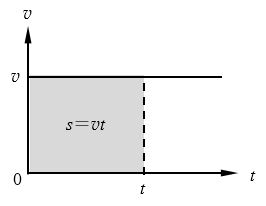
匀速直线运动的位移大小还可以在匀速直线运动的速度图象上反映出来。图3-21中，v-t图线与时间轴之间有一个矩形，这一矩形的一条边在数值上等于速度v的大小，另一条边在数值上等于时间t，这一矩形的面积等于矩形两条边的乘积v×t，所以，一个匀速直线运动在时间t内位移的大小，可以用它的速度图线与时间轴之间包围的面积来表示。

图象的意义

物理规律常用文字叙述，物理规律所揭示的物理量间的定量关系常用数学公式表达，这就使规律变得简单明了，便于进一步探讨各个变量间的关系；而用函数图象来表达规律所反映的变量关系时，则更能使这种关系得到形象直观的显示。因此，文字叙述、数学公式、函数图象是表述物理规律的几种基本手段，综合起来运用，人们便能更全面、确切、清晰地理解规律。

发布时间：2015/9/11 下午10:19:31  阅读次数：1660