F 匀加速直线运动
如果汽车行驶在平直的公路上,而你坐在汽车中观察速度计。当速度计的指针从零开始随时间均匀地顺时针转动刊10,20,30,…,这时汽车在做什么样的运动呢?
由于汽车在此运动中的瞬时速度随时间均匀增加,因此把这种运动叫做匀加速直线运动。
在前面的DIS中,我们已经看到过从轨道上滑下的小车做的也是这样的运动。
最早系统地研究匀加速直线运动的物理学家是伽利略(Galileo Galilei,1564-1642)。当时的实验条件很差,1604年他设计了一长约5.5m、宽约22cm的斜面,裱上一层羊皮纸,并用铜球做实验,如图1-45所示。时间测量是当时最大的困难,开始时他用自己的脉搏作为时间基准,后改用音乐的节拍,最后用水钟(根据水流来计时)。

实验中,伽利略不断改变铜球滚下的距离,重复了整整100次,结果“总是经过的距离与时间的平方成正比例,并且在各种不同坡度下进行实验,结果也都如此……”(伽利略语)
下面我们来讨论这种速度随时间均匀增加的直线运动。
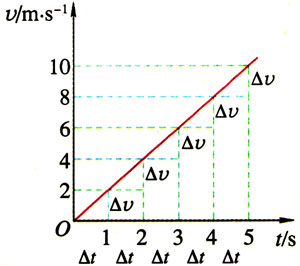
在前面用DIS测加速度的实验中,我们发现小车在轨道上下滑的v-t图是一条倾斜的直线。这种运动的特点是在相等的时间间隔Δt内,速度的增量Δv是相等的,如图1-46所示。
自主活动
请你根据图1 46所示v-t图,在图1-47中画出a-t图。
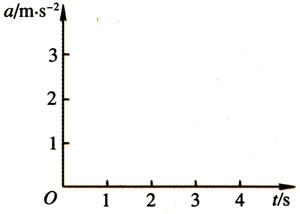
如果物体在直线运动中,速度从大到小随时间均匀减小,这种运动叫做匀减速直线运动。匀加速直线运动和匀减速直线运动都叫做匀变速直线运动。
从静止出发的匀加速直线运动,叫做初速度为零的匀加速直线运动。不是从静止出发的,即初速不为零的匀加速直线运动以及匀减速直线运动,我们在此不予讨论。
1.匀变速直线运动
速度随时间均匀变化的直线运动叫做匀变速直线运动。
匀变速直线运动是加速度大小和方向均不随时间变化的运动。
初速为零的匀变速直线运动遵循怎样的规律?
下面我们用图像和公式来探究这个问题。
探索研究
1.探究瞬时速度随时间变化的规律。由图1-46所示的v-t图中v与t的函数关系,写出瞬时速度vt的表达式。
_____________________________________________________。
2.探索位移随时间变化的规律。在得出位移公式时,请先阅读对图1-48的说明。
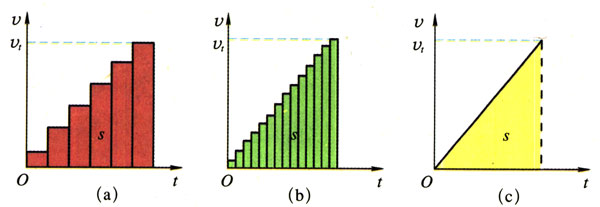
(b)若Δt取得更短,Δv也更小,则“台阶”变得很密,但t时间内位移仍然可以用图线下的面积来表示。
(c)当Δt变得极小时,“台阶”变成了一条直线。这就是匀变速直线运动的速度图线,图线下的三角形面积,表示t时间内位移的值。
图1-48
根据图1-48提供的思路请你导出位移s与时间t的关系式。
_______________________________________________________。
3.根据速度与时间关系式和位移与时间关系式,能否导出速度与位移的关系式?
_______________________________________________________。
2.初速为零的匀加速直线运动
(1)瞬时速度与时间的关系
vt=at
(2)位移与时间的关系
s=
(3)瞬时速度与加速度、位移的关系
vt=
示例 自行车的加速度为2m/s2,自静止出发,经3s后改做匀速直线运动,又向前运动了20s,求在这23s内自行车的总位移。
分析:本问题可分成两个过程来处理。自行车前3s(设为t1)做初速为零的匀加速直线运动,设位移为s1;后20s(设为t2)做匀速直线运动,设位移为s2。后一过程的速度v,就是前—过程的末速度。
解答:第一阶段自行车做初速为零的匀加速直线运动,则
s1=
第二阶段自行车做匀速直线运动,则
v=v1=at1=2×3m/s=6m/s,
s=vt2=6×20m=120m。
最后求得总位移s=s1+s2=(9+120)m=129m。
所以,自行车在23s内的总位移是129m。
讨论:本题能不能运用图像方法来解答?
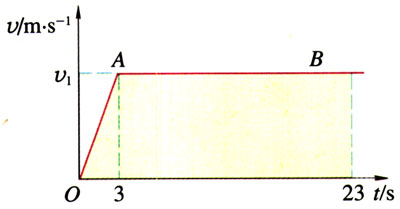
可以先画出v-t图(图1-49),总位移就是图线下的“面积”。由于图线OA的斜率(即加速度)是已知的,则v1=at=6m/s,于是三角形“面积”即前3s位移s1=
自主活动
试说明对初速度为零的匀加速直线运动:
(1)已知瞬时速度,怎样求平均速度?
(2)已知位移和运动时间,怎样求瞬时速度?
文件下载(已下载 204 次)发布时间:2015/9/4 下午9:21:07 阅读次数:1986
