A 热力学第一定律
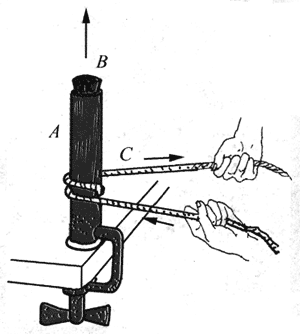
你看到过这样的表演吗?如图所示,在用台钳固定的薄铜管A中注入少量乙醚,盖紧橡皮塞B,然后在铜管下部绕一根绳子C,用双手来回抽动绳子,使绳子与管壁摩擦。不一会,就会听到“嘣”的一声,橡皮塞飞了出去。这里有摩擦力做功生热的问题,有热传递问题,有内能变化问题,还有气体做功问题。本节将要讨论做功、传热与内能变化之间存在的一个最普遍的定量关系,这个关系将力学和热学联系了起来。在这个规律的指引下,科学家和工程师有了许许多多新的发明和新的创造,将人类社会从马车和帆船时代推进到蒸汽机、内燃机、喷气发动机、汽轮机、火箭发动机的时代。
一、热力学第一定律
大家谈
在上图所示的实验中,发生了怎样的能量转化过程。
热和功之间的转化并不是直接进行的,其间必须经过某个物体或系统(如一定质量的气体)的内能的变化。例如上图的实验中,对于铜管来说,一方面绳子对它摩擦而做功,一方面铜管又对管内乙醚传递热量,在此功转化为热的过程中,铜管的内能有变化。同样,对于管内的乙醚来说,它一方面接受铜管传来的热量,一方面又对橡皮塞做功,在此热转化为功的过程中,管内乙醚的内能也有变化。
上述简单实验所揭示的热、功和内能之间的转化广泛存在于蒸汽机、内燃机、汽轮机、喷气发动机、火箭发动机,以及空调、冰箱、压缩机、抽气机等等统称为“热机”的工作过程中。
从基础型物理课程中已经知道,做功和热传递是改变物体或系统(如汽缸中的气体)内能的两条途经。那么我们要问:在这种热力学过程中,这些量之间存在怎样的定量关系?
设Ui、Uf,分别表示系统状态变化前、后的内能;在变化过程中,系统从外界吸收的热量为Q;外界对系统所做的功为W,则大量实验表明,它们之间满足如下普遍关系:
ΔU=Q+W,
其中ΔU=Uf-Ui是系统变化前后其内能的增量。这个关系式称为热力学第一定律,它表明:一个系统内能的增量等于它从外界吸收的热量与外界对它所做的功之和。它是自然界中的一切变化过程应当满足的一个普遍规律。
点击
本教材中,热力学第一定律表达式中三个物理量的正负号规定如下:系统吸热,Q>0;系统放热,Q<0。外界对系统做功,W>0;系统对外界做功,W<0。系统的内能增加,ΔU>0;系统的内能减少,ΔU<0。
热力学第一定律实际上是包括热现象在内的能量转化和守恒定律。从量上来说,它表示了物质运动的不可消灭性。能量不会凭空产生,也不会凭空消失。要使体系的能量增加,必须通过对它做功或加热,任何无中生有创造能量的企图都是不能实现的。从质上来说,该定律表示了各种能量相互转化的可能性,在一定条件下,内能和机械能是可以相互转化的。同时该定律也表明,热量传递和做功本质上是一样的,都是交换能量的一种方式。
【示例1】一定质量的物体,外界对它做了2.8×105J功,(1)如果它的内能增加4.2×105J,该物体吸收还是放出了热量?吸收或放出了多少热量?(2)如果它的内能增加1.6×105J,该物体吸收还是放出了热量?吸收或放出的热量又是多少?
【解答】(1)由热力学第一定律ΔU=Q+W,可得
Q=ΔU-W=(4.2×105-2.8×105)J=1.4×105J
Q为正,这表明该物体从外界吸收了1.4×105J热量。
(2)类似地可得
Q=ΔU-W=(1.6×105-2.8×105)J=-1.2×105J
Q为负,这表明该物体向外界放出了1.2×105J热量。
【讨论】如果本示例中已知一定质量的物体对外界做了2.8×105J功,则例中两个问题的答案是什么?
二、热力学第一定律对理想气体的应用
理想气体是热学中最简单的物理模型,有了这样一个具体例子,对于我们理解和思考热力学中的一般问题大有帮助。
利用热力学第一定律,对理想气体会得到哪些进一步的认识呢?
一定质量理想气体的状态可用三个状态参量:压强p、体积V、(绝对)温度T表示。此外内能也是一个状态参量。不过,这些状态参量不都是独立的,它们之间存在某些关系。
点击
一定质量理想气体的状态方程是
关于内能 从微观来看,物体的温度与分子热运动动能密切相关,温度是分子热运动平均动能的量度,分子平均动能越大,物体的温度就越高;反之亦然。对于理想气体,分子问的作用力可忽略不计,分子势能为零,因此一定质量理想气体的内能仅决定于它的温度。或者说,从理想气体温度的变化能确定它的内能的变化:温度升高,内能增加;温度降低,内能减小。由此可知,一定质量理想气体的“等温过程”中内能保持不变,而它的压强与体积则成反比。
这里还要指出,对理想气体状态的分析常常采用p-V图。从上一章的理想气体的状态方程可以看出,对于一定质量的理想气体来说,可从它的pV值的变化来判断其温度的变化,从而判断其内能的变化。(参见下面示例2)
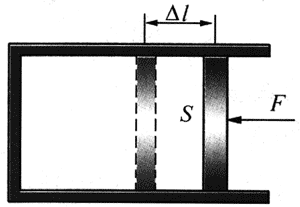
关于功 在力学中,“功”的定义是:功是力和位移的乘积。在热学中讨论得最多的是理想气体系统,研究的对象是封闭在汽缸中的理想气体,如图8-3所示。这时,理想气体的体积可通过活塞来改变。设活塞的面积为S,在外力F的作用下活塞移动了距离Δl,则外界对气体所做的功是W=FΔl=pSΔl,其中p=
W=pΔV。
可见,只有当理想气体的体积变化时,它才与外界有功的交换,在等压过程中,气体的压强不变,它的状态的变化可用p-V图上的一条平行于V轴的直线段表示,如图8-4所示。因此,理想气体等压过程中与外界交换的功最容易计算,它在数值上等于过程的p-V图线和V轴所围面积(功的正、负号应另加考虑)。
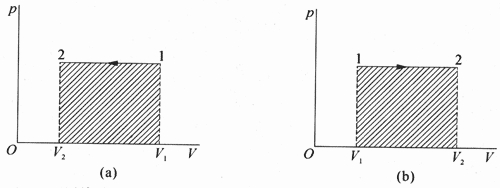
图8-4
【示例2】一定质量的理想气体在压强p不变的条件下,它的体积从V1膨胀到V2,此过程的p-V图如图8-4(b)所示。问此过程中气体与外界是否交换了热?是气体从外界吸收了热量,还是放出了热量?
【分析】为了考察理想气体在等压过程中与外界交换热量的情况,根据热力学第一定律ΔU=Q+W,需知道系统与外界交换功的情况以及系统内能的变化情况。前者可通过关系式W=pΔV来考察;后者可利用理想气体状态方程,由pV的变化了解温度T的变化,从而了解系统内能的变化。
【解答】气体在等压膨胀的过程中体积的改变量是ΔV=V1-V2,所以外界对系统做的功为
W=p(V1-V2)。
在等压膨胀过程中,V1<V2,因此外界对系统做的功W=p(V1-V2)=-p(V2-V1)<0,为负。这表明气体在等压膨胀过程中系统对外界做了功。
其次,根据理想气体状态方程(p不变):
ΔU>0。
再由热力学第一定律可知
Q=ΔU-W>0。
可见,一定质量理想气体在等压膨胀过程中必须从外界吸收热量。
【讨论】等压膨胀过程是一种吸热过程,此过程中系统从外界吸收热量,并将这些热量部分转化为向外输出的功,部分转化为气体的内能。用同样的方法还可考察等压压缩过程。
自主话动
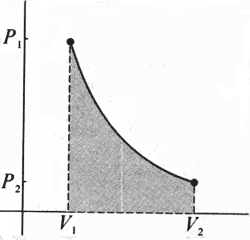
功的数值等于过程的p-V图线和V轴所围面积这个结论对于p不是恒定的过程,例如下图所示的等温过程,是否依然成立?说明之。
发布时间:2015/9/2 下午9:36:18 阅读次数:2511
