十、理想气体的内能变化

前面我们讲过了理想气体的等温、等容和等压变化，现在我们分析一下在这三种等值变化中内能的变化。

设一定质量的理想气体在温度不变的情况下发生膨胀，由初状态变到末状态。由于温度保持不变，所以气体的内能也不变，即ΔE＝0。气体发生膨胀时对外做功，所以W为负值，即W＜0。从热力学第一定律W＋Q＝ΔE＝0知道，Q应为正值。即Q＞0，而且W和Q的绝对值相等。可见，在等温膨胀的过程中，理想气体要从外界吸收热量，吸收的热量并没有增加气体的内能，而全部用来对外做功。

在体积不变的情况下，对一定质量的理想气体加热，使它的温度升高，压强增大，由初状态变到末状态。末状态的温度比初状态高，所以内能增加，即ΔE＞0。气体的体积不变，外界既没有对气体做功，气体也没有对外界做功，所以W＝0。根据热力学第一定律我们得到Q＝ΔE。可见，在等容变化中，如果理想气体从外界吸收热量，这个热量就全部用来增加气体的内能。

在压强不变的情况下，对一定质量的理想气体加热，使它的温度升高，体积增大，由初状态变到末状态，末状态的温度比初状态高，所以内能增加，即ΔE＞0。气体膨胀对外做功，W＜0。从热力学第一定律形W＋Q＝ΔE＞0知道，这时气体吸收的热量Q的绝对值大于W的绝对值。这就是说，在等压膨胀的过程中，理想气体从外界吸收的热量，一部分用来增加气体的内能，一部分用来对外做功。

除了上述三种等值变化外，还有一种所谓绝热变化在实际中常常遇到。物体在状态的变化过程中如果跟外界没有热交换，这种变化就叫做绝热变化。绝热变化的特点是：Q＝0。用绝热良好的材料把容器包起来，让气体发生膨胀或者对气体进行压缩，这时的变化就可以看作绝热变化。气体的膨胀或压缩进行得很迅速，从初状态到末状态所用的时间很短，气体来不及跟外界发生热交换，这种迅速的变化也可以看作绝热变化。图2-1所示的压缩气体的演示，热机气缸内气体膨胀做功，过程进行得很迅速，都可以看作绝热变化。在绝热压缩的过程中，外界对气体所做的功完全用来增加气体的内能，使气体的温度升高。在绝热膨胀的过程中，气体对外界做功完全靠气体内能的减少，因而气体的温度降低。

练习七

（1）一定质量的理想气体在温度不变的情况下被压缩，气体的内能是否改变？外界对气体是否做功？气体从外界吸热还是向外界放热？功和热量有什么关系？

（2）一定质量的理想气体在体积不变的情况下压强减小，这时外界对气体是否做功？气体的内能是否改变，怎样改变？气体放出的热量跟内能的改变有什么关系？

（3）一定质量的理想气体在压强不变的情况下体积减小，外界对气体是否做功？气体的内能是否改变，怎样改变？气体放热还是吸热？这个热量跟内能的改变有什么关系？

复习题

（1）哪几个物理量是描述气体的状态参量？

（2）什么叫等温变化？玻意耳-马略特定律的内容是什么？写出它的表达式。

（3）什么叫等容变化？查理定律的内容是什么？写出它的表达式。

（4）什么叫等压变化？盖·吕萨克定律的内容是什么？写出它的表达式。

（5）写出任意质量的理想气体的状态方程即克拉珀龙方程，并作为特例推出：1摩的理想气体的状态方程，质量一定但不知道质量数值时理想气体的状态方程，（2）、（3）、（4）中的三个气体实验定律。

（6）你自己总结一卞用理想气体状态方程解题的基本思路和步骤以及要注意的问题。

（7）气体分子运动的特点是什么？从分子运动论的观点看来，气体压强是怎样产生的？它的大小是由什么决定的？

（8）用气体分子运动论对三个气体实验定律作出微观解释。

（9）理想气体的微观模型是怎样的？为什么理想气体的内能只跟温度有关，而跟体积无关？

（10）*试分别说明理想气体在等温、等容、等压变化中内能变化的情形。

习题

（1）下面几种说法，哪个正确，哪个错误，并说明理由。

①有两个相同的容器，内装同种气体，它们的压强相同，因而它们的温度一定相同。

②有两个相同的容器，内装质量相同的不同气体，它们的压强不同，因而它们的温度一定不同。

③有两个相同的容器，内装摩尔数相同的气体，它们的压强相同，因而它们的温度一定相同。

（2）一定质量的理想气体，处在某一初始状态。现在要使气体的温度经过状态变化后回到初始状态的温度，用下列哪些过程可能实现？

①先保持压强不变而使它的体积膨胀，接着保持体积不变而减小压强。

②先保持压强不变而使它的体积减小，接着保持体积不变而减小压强。

③先保持体积不变而增大压强，接着保持压强不变而使它的体积膨胀。

④先保持体积不变而减小压强，接着保持压强不变而使它的体积膨胀。

（3）盖·吕萨克定律如果用摄氏温标t来表示，可以写成下式：

V_t＝V₀（1＋t/273）。

其中V₀和V_t分别表示气体在0℃和t℃时的体积。试推导出上式。

（4）能不能根据玻意耳-马略特定律和盖·吕萨克定律推出一定质量的理想气体的状态方程pV/T＝恒量？实际椎导一下。

（5）当温度为27℃、压强为2.0×10⁵Pa时，32g氧气的体积是多大？密度是多大？？另有48g氧气，温度和压强跟上述数值相同，氧气的密度又是多大？

（6）试根据克拉珀龙方程推导出用压强和温度来表示的气体密度的表达式。

（7）水银气压计中混入了一个空气泡，上升到水银柱的上方，使水银柱上方不再是真空，因而气压计的读数比实际的大气压小些。当实际大气压为768mmHg时，气压计的读数只有750mmHg，此时管中水银面到管顶的距离为80mm。当气压计读数为740mmHg时，实际大气压为多少？设温度保持不变。

（8）在湖面下50m深处（温度为4℃）有一个体积为10cm³的气泡升到湖面上来，湖面的温度为17℃。求它升到湖面时的体积。大气压强为1.013×10⁵Pa。

（9）有两个容积相等的容器，里面盛有同种气体，用一段水平玻璃管把它们连结起来。在玻璃管的正中央有一段水银柱，当一个容器中气体的温度是0℃，另一个容器中气体的温度是20℃时，水银柱保持静止。如果使两容器中气体的温度都升高10℃，管中的水银柱会不会移动？如果移动的话，向哪个方向移动？试根据学过的气体定律加以说明。

（10）一个容器，如果其中气体十分稀薄，通常就说这个容器为“真空”。有一个容积为10cm³的电子管，在温度为300K时用真空泵把它抽成真空，使管内气体压强为5×10^-6mmHg。这时管内有多少个气体分子？

（11）氧气瓶的容积是32L，其中氧气的压强是130标准大气压，规定瓶内氧气压强降到10标准大气压时就要重新充氧。有一个车间，每天需用1标准大气压的氧气400L。这瓶氧气能用几天？假定温度保持不变。

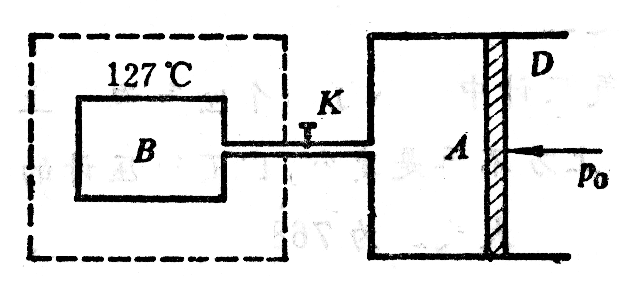
（12）如图3-16所示，气缸A和容器B由一细管经阀门K相联。A和B的壁都是透热的。A放在27℃、1标准大气压的大气中，B浸在127℃的恒温槽内。开始时K是关断的，B内没有气体，容积V_B＝2.4L；A内装有气体，体积V_A＝4.8L，打开K，使气体由A流入B，等到活塞D停止移动时，A内气体的体积是多大？假设活塞D与气缸壁之间没有摩擦，细管的容积忽略不计。

发布时间：2015/8/28 上午8:37:10  阅读次数：8667