八、气体实验定律的微观解释

气体压强的微观解释 从气体分子运动论的观点看来，气体压强是大量的气体分子频繁地碰撞器壁而产生的。雨滴打在雨伞上，使伞面受到冲力。单个雨滴对伞面的冲力是短暂的，但大量密集的雨滴接连不断地打在伞面上，对伞面就形成一个持续的均匀的压力。同样，单个分子碰撞器壁的冲力是短暂的，但是大量分子频繁地碰撞器壁，就对器壁产生持续的均匀的压力。下面我们从气体分子运动论的观点定性地讨论一下气体的压强。

设想容器内只有一个分子，我们可以利用以前学过的力学知识算出这个分子碰撞器壁时对器壁产生多大的冲力，现在的问题是：容器中有大量分子，它们的速度的大小和方向又不断地在改变。怎样才能算出大量分子碰撞器壁时对器壁产生的冲力呢？

我们知道，气体分子做无规则运动，它们沿各个方向运动的机会是均等的，也就是说，在上下、前后、左右各个方向中没有哪个方向的运动占优势。因此我们可以认为各有1/6的分子向着上下前后左右这六个方向运动。气体分子速度的大小也不相同，但我们可以认为所有分子都以平均速率向着各个方向运动。

现在设想有一个向右运动的分子与器壁发生碰撞（图3-14）。碰撞前的动量是mv，其中v是分子的平均速率。碰撞后向左运动，速率是vʹ，动量是－mvʹ。这个分子碰撞前后的动量变化是－mvʹ－mv，气体分子与器壁之间的碰撞是完全弹性碰撞，这样，分子碰撞前后的速率相等，即vʹ＝v，因而动量变化是－2mv。从动量定理知道，这个动量变化－2mv等于器壁对分子的冲量。从牛顿第三定律知道，这时分子对器壁也有一个大小相等方向相反的冲量。可见气体分子每碰撞一次器壁，就给器壁2mv的冲量。

在一段时间内，大量分子与器壁碰撞多少次，分子给器壁的总冲量就是2mv的多少倍。而在单位时间内分子给器壁的总冲量就等于器壁所受的压力，单位面积器壁所受的压力就等于气体的压强。

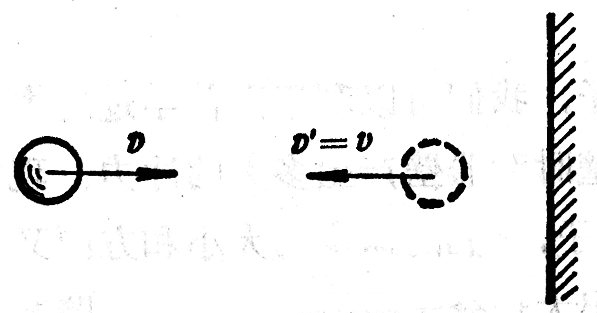
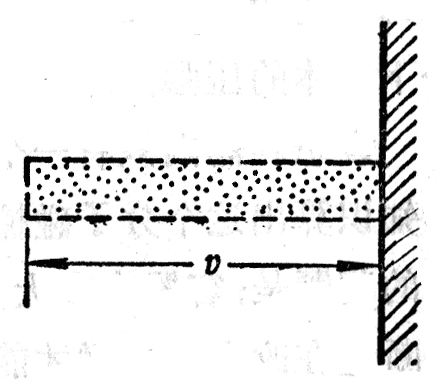
这样，如果知道单位时间内分子对单位面积器壁的碰撞次数，就可以求得气体的压强。这个碰撞次数跟单位体积内气体的分子数有关。单位体积内气体的分子数越多，即气体分子越密，这个碰撞次数就越多。这是容易理解的，这个碰撞次数还跟分子的平均速率有关。如图3-15所示，我们在气体内部设想一个柱体，底面积为单位面积，高为平均速率的数值。在单位时间内，这个柱体中向右运动的分子都会运动到器壁而发生碰撞。平均速率越大，这个柱体越高，其中的分子越多，分子与器壁发生碰撞的次数就越多。可见，单位时间内分子对单位面积器壁的碰撞次数是由单位体积内的分子数和分子的平均速率决定的。由此我们将不难理解气体压强也是由单位体积内的分子数和分子的平均速率决定的。单位体积内的分子数越多，分子的平均速率越大，气体的压强就越大。

气体实验定律的微观解释 知道了气体压强是由什么决定的，我们就能够用气体分子运动论对气体实验定律作出微观解释。

一定质量的气体，温度保持不变，也就是分子的总数和分子的平均速率保持不变。在这种情况下，气体的体积减小到原来体积的几分之一，单位体积内的分子数就增大到原来的几倍，气体的压强就增大到几倍。气体体积增大时，情况恰好相反，结果是气体的压强与体积成反比。这就是玻意耳-马略特定律。

用气体分子运动论也可以解释查理定律。一定质量的气体，体积保持不变而温度升高时，分子的平均速率增大，因而气体的压强增大。温度降低时，情况恰好相反。

怎样解释盖·吕萨克定律呢？从气体分子运动论可以说明：一定质量的气体温度升高时，要保持压强不变，只有让气体的体积增大才行。这时，一方面由于温度升高，分子的平均速率增大，以致每次碰撞给器壁的冲量增加，同时单位时间内对单位面积器壁的碰撞次数增多，使压强有增大的倾向；另一方面，由于体积增大，单位体积内的分子数减少，以致单位时间内分子对单位面积器壁的碰撞次数减少，使压强有减小的倾向。当体积增大到一定程度时，这两种倾向抵消，所以压强保持不变。

气体分子运动论不仅能够解释上述气体实验定律，而且能够解释气体的其他一些性质，如气体的比热、扩散、热传导等。气体分子运动论是热学和分子物理学的重要组成部分，它使人们对气体的研究从宏观领域进入微观领域，扩展和加深了人们对气体性质的认识。

练习六

（1）现在我们用另一种方法估算一下气体分子间的距离与分子直径的关系。在标准状态下，1摩的气体占有22.4升的体积。我们设想其中的每个分子都位于一个小立方体的中心。这个小立方体的边长是多少？分子直径的数量级为10^-10米。把小立方体的边长跟分子直径相比较，结果怎样？

（2）根据第七节表中的数据能不能估算出℃和100℃时氧气分子的平均速率？怎样估算？结果怎样？

发布时间：2015/8/26 下午6:10:02  阅读次数：2088