五、理想气体的状态方程

前面我们研究了一定质量的气体在温度不变时压强跟体积的关系以及体积不变时压强跟温度的关系，分别得出了玻意耳-马略特定律和查理定律。现在我们从这两个实验定律出发，确定一定质量的气体的体积、压强、温度这三个状态参量在变化中的相互关系。

设有一定质量的气体，在初状态时的压强、体积和温度分别为p₁，V₁，T₁，经过某个变化过程，到末状态时这三个量分别变成p₂，V₂，T₂。气体从初状态到末状态可以经过各种不同的变化过程，现在设想有一个变化过程是分两个阶段进行的。在第一个阶段中，保持温度T₁不变，体积从V₁变成V₂，压强从p₁变成另一个值p_c（图3-12中的1和2）。在第二个阶段中，保持体积V₂不变，温度从T₁变成T₂，压强从p_c变成p₂（图3-12中的2和3）。

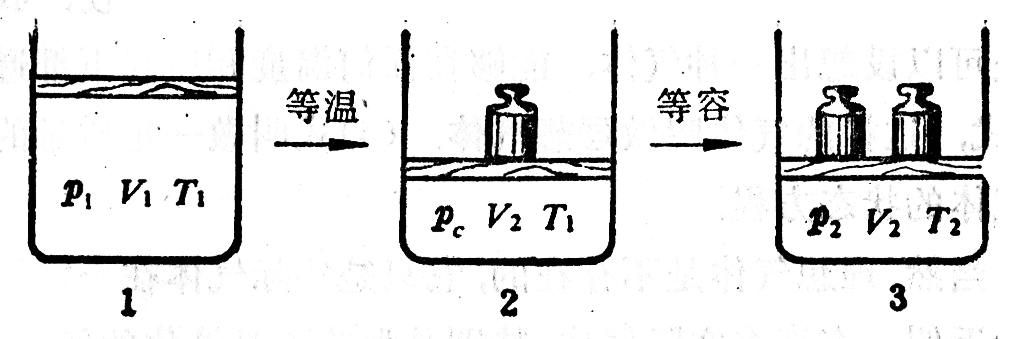
第一个阶段是等温变化，根据玻意耳-马略特定律有

p₁V₁＝p_cV₂。        （1）

第二个阶段是等容变化，根据查理定律有

\(\frac{{{p_c}}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}}\)           （2）

由（1）式解出p_c，代入（2）式，整理后得到

\(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\)。            （3）

上式说明，一定质量的气体从初状态（p₁，V₁，T₁）变到末状态（p₂，V₂，T₂），压强和体积的乘积与热力学温度的比值是不变的，即

\(\frac{{pV}}{T}\)＝恒量。        （4）

我们知道，玻意耳-马略特定律和查理定律是在压强不太大、温度不太低的条件下总结出来的。在这种条件下，不论什么气体都近似地符合这两个实验定律。（4）式是从上述两个实验定律推导出来的，因此，也只有在这种条件下，不论什么气体才近似地符合（4）式。尽管如此，为了研究的方便，我们还是可以设想出一种气体，能够在任何温度和压强下都遵守（4）式，这样的气体叫做理想气体。（4）式叫做一定质量的理想气体的状态方程。

当然，理想气体是不存在的，它只是实际气体在一定程度上的近似。有许多实际气体，特别是那些不易液化的气体，如氢气、氧气、氮气、空气、氦气等，在通常的温度和压强下，它们的性质很近似于理想气体，可以把它们当作理想气体来处理，这样处理的结果，误差很小，可是计算起来却简便多了。

理想气体状态方程实际上包含了前面讲的两个气体实验定律。如果保持温度T不变，便得到pV＝恒量，这就是玻意耳-马略特定律，如果保持体积V不变，便得到p/T＝恒量，这就是查理定律。

从理想气体状态方程还可以知道，压强保持不变时，一定质量气体的体积怎样随着温度而变化，这种变化叫做等压变化。在保持压强p不变时，得到V/T＝恒量，这表示压强不变时，一定质量气体的体积跟热力学温度成正比。这个关系最初是法国科学家盖·吕萨克（1778 ～1850）研究气体热膨胀时得到的实验定律，叫做盖·吕萨克定律。在压强不太大、温度不太低时，不论什么气体都近似地符合这个定律。

练习四

（1）对一定质量的气体来说，能否做到：①保持压强和温度不变而改变它的体积？（多保持温度和体积不变而改变它的压强？②保持体积和压强不变而改变它的温度？

（2）对一定质量的气体来说，能否做到：①保持压强不变，同时升高温度并减小体积？②保持温度不变，同时增加体积并减小压强？③保持体积不变，同时增加压强并降低温度？

（3）一定质量的空气，27℃时的体积为1.0×10^-2m³。计算在压强不变的情况下，温度升高到100℃时的体积。

（4）某种柴油机的气缸容积为0.83×10^-3m³。压缩前其中空气的温度为47℃，压强为0.8×10⁵Pa。在压缩冲程，活塞把空气压缩到原体积的1/17，压强增大到40×10⁶Pa。求这时空气的温度。

（5）在容积为25L的容器中，盛有温度为37℃、压强为62标准大气压的氧气。求氧气在标准状态（0℃，1标准大气压）下的体积。从化学课中学过，在标准状态下，1摩的任何气体的体积都是22.4L。你能不能由此求得容器中氧气的摩尔数并进而求得氧气的质量？怎样求？

（6）一个瓶子里装有某种气体，瓶上有一个小孔跟外面大气相通，原来瓶里气体的温度为15℃。如果把它加热到207℃，瓶里保留的气体的质量是原来质量的几分之几？

（7）贮气筒内装有压缩气体，温度是27℃，压强是40×10⁶Pa。如果从筒内放出一半质量的气体，并使筒内剩余的气体的温度降到12℃，这些剩余气体的压强是多大？

发布时间：2015/8/23 下午3:50:15  阅读次数：2567