四、热力学温标

图3-10表明了气体的压强跟温度之间的关系。我们看到，图中的直线并未通过原点，说明气体的压强不是直接与摄氏温度成正比的，但是如果我们改用一个新的温标，那就可以得到压强和温度之间的简单的正比关系。

把图3-10中的直线向左方延长，交横轴于D点（图3-11），D点表示气体的压强等于零时的温度，这个温度是多少度呢？

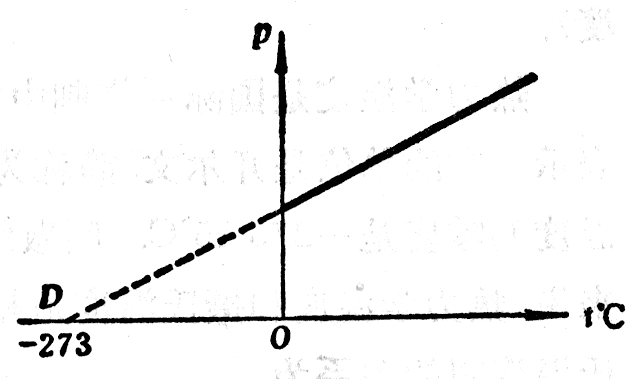
设p_t＝p₀（1＋\(\frac{t}{{273}}\)）＝0，由于p₀≠0，所以必须要求1＋\(\frac{t}{{273}}\)＝0，由此得出t＝－273℃。

精确的实验证明，上节查理定律数学表达式中的273应该是273.15。这样，气体压强等于零时的温度就应该是－273.15℃。

英国科学家威廉·汤姆孙（开尔文）（1824～1907）创立了把－273.15℃作为零度的温标，叫做热力学温标（或绝对温标），用热力学温标表示的温度叫做热力学温度（或绝对温度）。

热力学温度是国际单位制中七个基本量之一，用符号T表示，它的单位是开尔文，简称为开，国际符号为K。热力学温度的零度是－273.15℃叫做绝对零度，就每一度的大小来说，热力学温度和摄氏温度是相同的，所以热力学温度跟摄氏温度间的关系为

T＝t＋273.15。

为了简化，可以粗略地取－273℃为绝对零度，这样就有

T＝t＋273。

例如，在1标准大气压下，冰的熔点为0℃即273K，水的沸点为100℃即373K。

利用热力学温标可以使查理定律的表述简化。设在体积不变的情况下，一定质量的气体温度为t₁时压强为p₁，温度为t₂时压强为p₂，那么

\[\begin{array}{l}{p_1} = {p_0}(1 + \frac{{{t_1}}}{{273}}) = {p_0}\frac{{273 + {t_1}}}{{273}}\\{p_2} = {p_0}(1 + \frac{{{t_2}}}{{273}}) = {p_0}\frac{{273 + {t_2}}}{{273}}\end{array}\]

其中p₀表示0℃时的压强。把上面两式相除得到

\[\frac{{{p_1}}}{{{p_2}}} = \frac{{273 + {t_1}}}{{273 + {t_2}}}\]

用热力学温度T₁和T₂分别代换（273＋t₁）和（273＋t₂），得到

\[\frac{{{p_1}}}{{{p_2}}} = \frac{{{T_1}}}{{{T_2}}}\]

可见查理定律可以表述为：体积不变时，一定质量的气体的压强跟热力学温度成正比。

上面是把查理定律“外推”到零压强而引入热力学温标的。这种“外推”是可以理解的。随着温度的降低，气体分子热运动减弱，分子对器壁的撞击作用也减弱，因而压强减小。由此推想，在某一个温度下，气体压强变为零，这个温度就是绝对零度。实际上，在达到绝对零度之前，任何气体都已液化甚至变为固体，查理定律早已不适用了。虽然如此，由“外推”得到的绝对零度仍具有物理意义，它是低温的极限，能够无限接近，但不可能达到。

练习三

（1）炎热的夏天，打足了气的自行车胎在日光曝晒下有时会胀破。解释这个现象。

（2）乒乓球挤瘪后，放在热水里泡一会，会重新鼓起来。解释这个现象。

（3）一定质量的氢气在0℃时的压强是700mmHg，它在30℃时的压强是多大？压强为650mmHg时它的温度是多少摄氏度？保持氢的体积不变。

（4）一定质量的某种气体，在20℃时的压强是1.0×10⁵Pa。如果保持它的体积不变，温度升高到50℃时，它的压强是多大？温度降低到－7℃时，它的压强又是多大？

（5）盛有氧气的钢筒，在室内（室温是17℃）测得筒内气体的压强是9.31×10⁶Pa。当钢筒搬到温度是－13℃的工地时，筒内气体的压强变为8.15×10⁶Pa，钢筒是不是漏了气？为什么？

（6）装在容器中的气体，体积为4L，压强为2.0×10⁵Pa，温度为300K，先让气体发生等容变化，压强增大为原来的2倍。然后让气体发生等温变化，压强又降低到原来的数值。求气体在末状态时的体积和温度。

发布时间：2015/8/23 下午3:49:35  阅读次数：1091