二、气体的等温变化 玻意耳-马略特定律

我们先来研究温度不变时，一定质量的气体的压强随着它的体积而变化的情形，这种变化叫做等温变化。

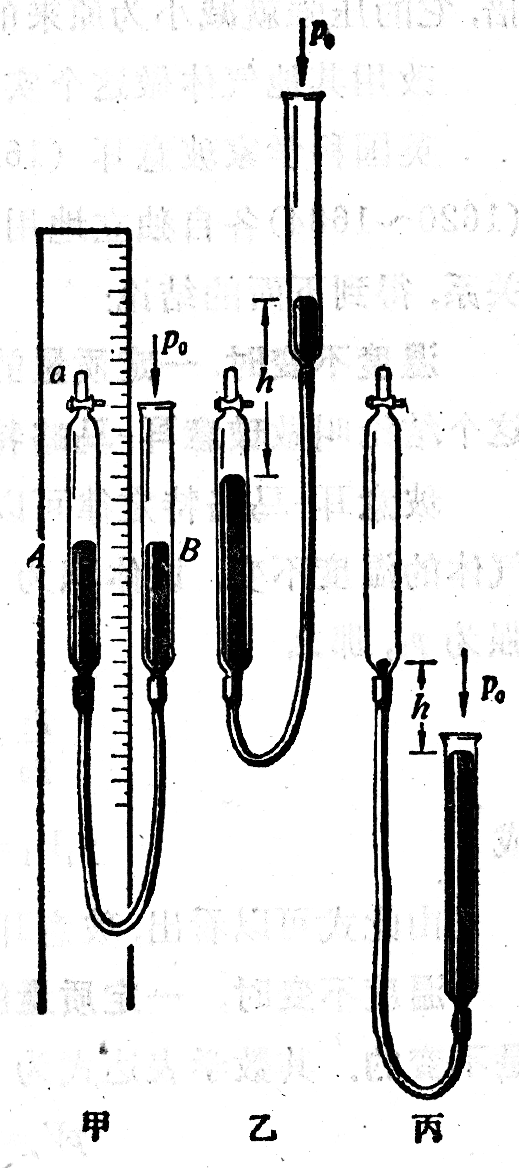
实验装置如图3-5所示，玻璃管A和B通过一条橡皮管连在一起。A管上端有一个阀门a，B管上端是开口的。A管固定在有刻度的竖直板上，B管可以上下移动。实验开始时，打开阀门a，从B管注入水银，然后关闭阀门，把一定质量的空气封闭在A管里，当两管中的水银面一样高时（图甲），A管里空气的压强等于作用在B管水银面上的大气压。

把B管慢慢提高，使A管里空气的体积缩小，这时B管里的水银面比A管里的高（图乙），A管里气体的压强等于大气压加上B管水银面高出A管水银面的那段水银柱的压强。实验表明，在温度不变的条件下，气体的体积缩小到原来的几分之一，它的压强就增大到原来的几倍。

把B管慢慢放低，使A管里气体的体积增大，这时B管里的水银面比A管里的低（图丙），A管里气体的压强等于大气压减去A管水银面高出B管水银面的那段水银柱的压强。实验表明，在温度不变的条件下，气体的体积增大到原来的几倍，它的压强就减小为原来的几分之一。

改用其他气体做这个实验，得到的结果相同。

英国科学家玻意耳（1627～1691）和法国科学家马略特（1620～1684）各自独立地用实验研究了气体的压强和体积的关系，得到下面的结论：

温度不变时，一定质量的气体的压强跟它的体积成反比。这个结论叫做玻意耳-马略特定律。

玻意耳-马略特定律可以用公式来表示。保持一定质量气体的温度不变，设体积为V₁时压强为p₁，体积为V₂时压强为p₂，那么

\[\frac{{{p_1}}}{{{p_2}}} = \frac{{{V_2}}}{{{V_1}}}\]

或                                                     p₁V₁＝p₂V₂。

由此式可以看出，玻意耳-马略特定律也可以叙述为：

温度不变时，一定质量的气体的压强跟它的体积的乘积是不变的。其数学表达式为

pV＝恒量。

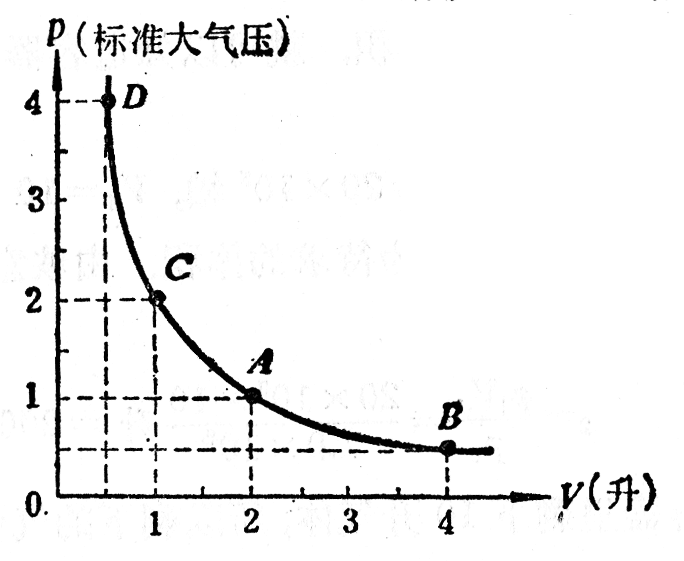
气体的等温变化也可以用图线来表示，用直角坐标系的横轴表示气体的体积V，用纵轴表示气体的压强p。设在一定温度下，一定质量的某种气体在V₁＝2升时，p₁＝1标准大气压，在图3-6中由A点表示。根据玻意耳-马略特定律可以得出：V₂＝4升时，p₂＝1/2标准大气压，由B点表示；V₃＝1升时，p₃＝2标准大气压，由C点表示；V₄＝1.2升时，p₄＝4标准大气压，由D点表示。当然还可以使气体的体积等于其他许多不同的数值，并计算出相应的压强的数值，从而得到其他许多点。由这些点连成的平滑曲线，叫做气体的等温线。从等温线可以清楚地看出温度不变时气体的压强跟体积的关系。

【例题】某个容器的容积是10L，所装气体的压强是20×10⁵Pa，如果温度保持不变，把容器的开关打开以后，容器里剩下的气体是原来的百分之几？设大气压是1.0×10⁵Pa。

这个题目可以这样来分析。容器里装着一定质量的气体。取这一定质量的气体作为我们的研究对象。气体在初状态时，p₁＝20×10⁵Pa，V₁＝10L。打开开关以后，由于气体压强大于外界大气压，于是气体发生膨胀（等温膨胀），有一部分气体跑出容器。随着气体的膨胀，气体的压强降低，最后，当气体压强等于外界大气压时，气体停止膨胀而达到末状态，这时，气体一部分在容器内，一部分在容器外。如果我们知道气体在末状态时占有多大体积，就可以知道容器里剩下的气体为原来的百分之几。

气体在初状态时，p₁＝20×10⁵Pa，V₁＝10L。在末状态时，p₂＝1.0×10⁵Pa，V₂为待求的体积。由玻意耳-马略特定律p₁V₁＝p₂V₂得到

V₂＝\(\frac{{{p_1}{V_1}}}{{{p_2}}}\)＝\(\frac{{20 \times {{10}^5} \times 10}}{{1.0 \times {{10}^5}}}\)L＝200L。

这时容器里剩下10L气体，所以剩下的气体是原来气体的10L/200L＝5%。

从这里我们看到，利用玻意耳-马略特定律来解题，先要明确研究对象以及它的初末两个状态，然后才能利用公式来求解。用玻意耳-马略特定律解题时，还要注意等式两边的p或V必须采用相同的单位，至于具体采用什么单位，可以根据解题方便来决定。

玻意耳-马略特定律表示一定温度下气体的压强跟体积的关系，因此我们可以预料这个定律的表达式

pV＝恒量

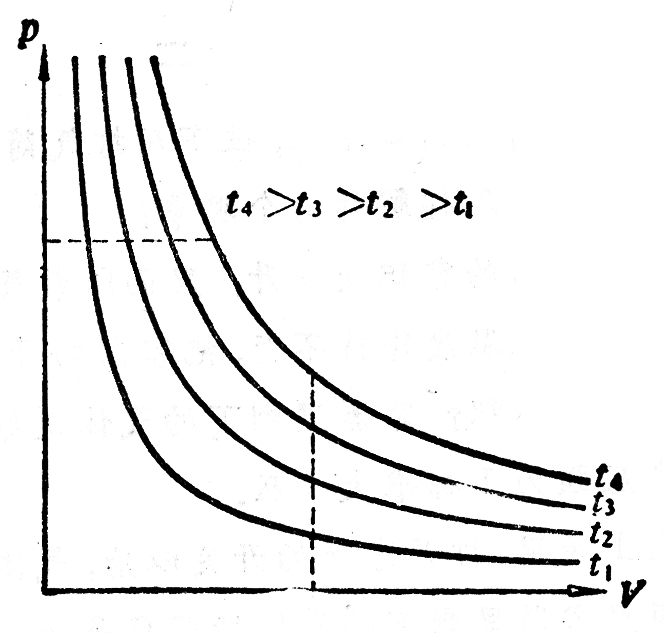
中的恒量跟温度有关系。实验表明，温度不同，这个恒量也不同。图3-7中画出了不同温度下的几条等温线，从此可以知道：一定质量的气体，保持它的体积不变，温度越高，压强越大；保持它的压强不变，温度越高，体积越大。可见，表达式中的恒量随温度而增大，这样看来，要确定体积、压强、温度这三个物理量的变化规律，我们还需要研究压强怎样随着温度而变化或者体积怎样随着温度而变化。

玻意耳-马略特定律是在压强不太大（和大气压比较）、温度不太低（和室温比较）的条件下总结出来的。在这种条件下，不论什么气体都近似地符合这个定律。当压强很大、温度很低时，由这个定律得出的结果跟实际测量的结果有很大差别，这个定律就不适用了。举例来说，有一定质量的氦气，压强为1标准大气压时，体积为1米³。压强为500标准大气压时，按照玻意耳-马略特定律体积应该是1/500米₃，而实际测量的结果是1.36/500米³，二者之间已经显示出不小的差别。压强为1000标准大气压时，按照玻意耳-马略特定律体积应该是1/1000米³，而实际测量的结果是2.0685/1000米³，二者相差一倍多，根本无法应用玻意耳-马略特定律了。

练习二

（1）把打气筒的出口堵住，往下压打气筒的活塞，会感到越往下压越费劲，怎样解释这个现象？

（2）某个容器的容积是5L，里面所装气体的压强是10标准大气压，如果温度保持不变，把容器的开关打开以后，这些气体会有多大体积？容器里剩下的气体是原来的百分之几？设外界压强为1标准大气压。

（3）在上题里，打开容器的开关以后，气体的密度怎样改变？设上题里容器里剩下的气体的密度是ρ₂，原来容器里气体的密度是ρ₁，那么，密度之比ρ₂/ρ₁是多大？

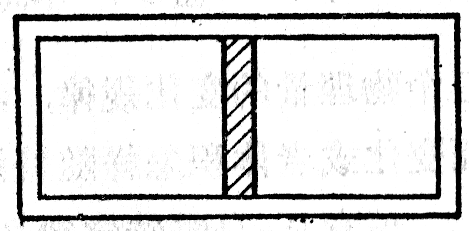
（4）在密闭圆筒的中央有一个活塞（图3-8），活塞两边封闭着两部分气体，它们的压强都是750毫米汞柱。现在用力把活塞向右移动，使活塞右边气体的体积为原来的一半，那么活塞两边气体的压强差是多大？假定气体的温度不变。

（5）在图3-2中，水银柱的长度为19cm，大气压为760mmHg。玻璃管是粗细均匀的。玻璃管开口向上竖直放置时，被封闭的气体柱长15cm，当开口向下竖直放置时，被封闭的气体柱的长度是多少？

（6）在下端封闭的竖直玻璃管里有一段4cm长的水银柱，水银柱下面封闭着6cm³的空气。玻璃管的横截面积是0.1cm²。如果再向管里装入27.2g水银，郡么，封闭在水银柱下面的空气柱有多高？设大气压为760mmHg。

（7）一个足球的容积是2.5L，用打气筒给这个足球打气，每打一次就把1标准大气压的空气打进去125cm³。如果足球在打气前内部没有空气，打了40次以后，足球内部空气的压强有多大？假定空气的温度不变。

发布时间：2015/8/21 上午9:00:51  阅读次数：2683